Четырёхмерный куб

Содержание.
1.Объект исследования
2.Цель исследования
3.Исследование
4.Результат исследования
5.Использованная литература

Как его увидеть
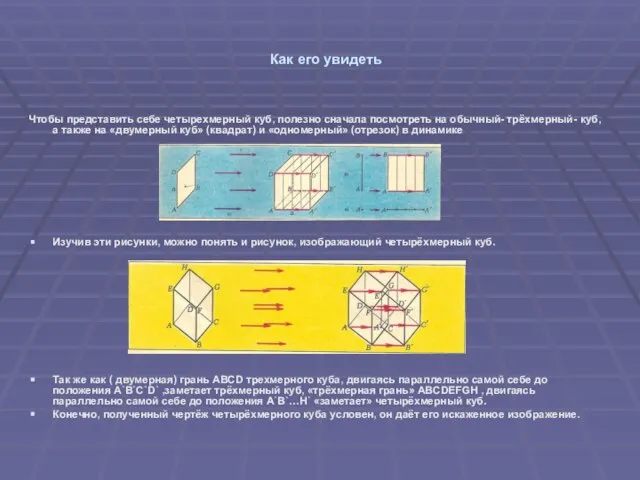
Чтобы представить себе четырехмерный куб, полезно сначала посмотреть на обычный- трёхмерный- куб, а также на «двумерный куб» (квадрат) и «одномерный» (отрезок) в динамике
Изучив эти рисунки, можно понять и рисунок, изображающий четырёхмерный куб.
Так же как ( двумерная) грань ABCD трехмерного куба, двигаясь параллельно самой себе до положения A`B`C`D` ,заметает трёхмерный куб, «трёхмерная грань» ABCDEFGH , двигаясь параллельно самой себе до положения A`B`…H` «заметает» четырёхмерный куб.
Конечно, полученный чертёж четырёхмерного куба условен, он даёт его искаженное изображение.

Как его развернуть:
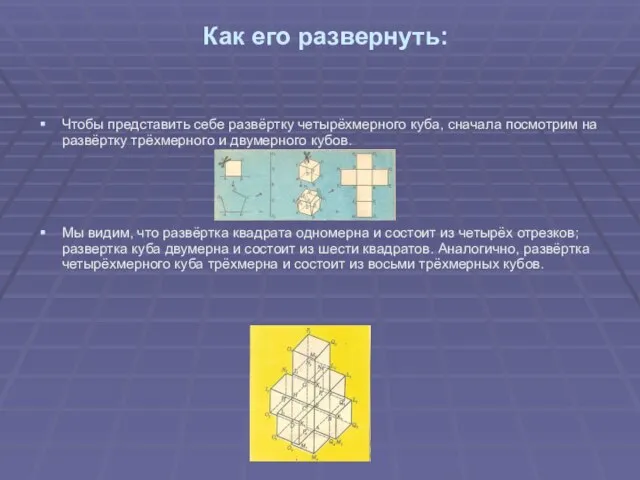
Чтобы представить себе развёртку четырёхмерного куба, сначала посмотрим на развёртку трёхмерного и двумерного кубов.
Мы видим, что развёртка квадрата одномерна и состоит из четырёх отрезков; развертка куба двумерна и состоит из шести квадратов. Аналогично, развёртка четырёхмерного куба трёхмерна и состоит из восьми трёхмерных кубов.

Дом, который построил Тил
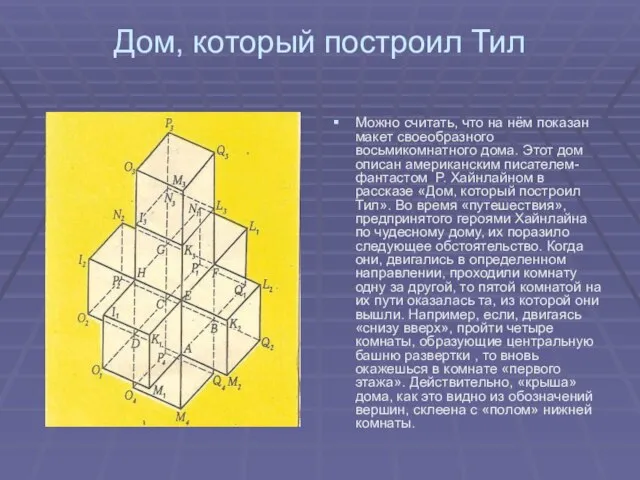
Можно считать, что на нём показан макет своеобразного восьмикомнатного дома. Этот дом описан американским писателем-фантастом Р. Хайнлайном в рассказе «Дом, который построил Тил». Во время «путешествия», предпринятого героями Хайнлайна по чудесному дому, их поразило следующее обстоятельство. Когда они, двигались в определенном направлении, проходили комнату одну за другой, то пятой комнатой на их пути оказалась та, из которой они вышли. Например, если, двигаясь «снизу вверх», пройти четыре комнаты, образующие центральную башню развертки , то вновь окажешься в комнате «первого этажа». Действительно, «крыша» дома, как это видно из обозначений вершин, склеена с «полом» нижней комнаты.

Как его спроектировать
Существует ещё один популярный способ изображения четырёхмерного куба.
Восемь трёхмерных граней изображены здесь внутренним (малым) кубом, внешним (большим) кубом и шестью усеченными пирамидами, соединяющими соответственные грани малого и большого кубов. Этот рисунок получается при центральном проектировании четырёхмерного куба на некоторую «трёхмерную плоскость»
По рисунку удобнее всего сосчитать количество разного рода составляющих элементов четырёхмерного куба. Он имеет 16 вершин,32 ребра, 24 двумерных грани ( в виде квадратов) и 8 «трёхмерных граней» (в виде кубов).

Как его строго определить
Прежде, чем давать это определение, мы приведём несколько хорошо известных наблюдений.
Отрезок ( одномерный куб) располагается на прямой ( в одномерном пространстве) и в системе координат ox может быть задан неравенством 0< x <1
Квадрат (двумерный куб) располагается на плоскости (в двумерном пространстве) и в системе координат oxy может быть задан системой неравенств 0< x <1, 0
Трёхмерный куб в системе координат Oxyz трёхмерного пространства выделяется системой неравенств 0

Эти наблюдения делают естественным такое определение.
Четырёх мерный куб- это множество всех четверок действительный чисел (x; y; z; t;), для которых 0
Где у каждой вершины указаны её координаты.
Четырёхмерным пространством называется множество всех четверок чисел (x; y; z; t), где x, y, z, t – действительные числа, для которых определено расстояние по формуле

С определением плоскости в четырёхмерном пространстве дело обстоит не так просто. Дело в том, что здесь бывают как обычные двумерные плоскости, так и трёхмерные плоскости, называемые гиперплоскостями. С точки зрения задания плоскостей уравнениями, именно гиперплоскость является точным аналогом обычной плоскости в трёхмерном пространстве. В уравнении Ax+By +Cz+D=0 обычной плоскости двум из трёх переменных x, y, z, можно придавать произвольные значения, и тогда значение третьей переменной будет определяться из уравнения однозначно. Таким образом, множество всех решений этого уравнения описывается двумя произвольными параметрами, то есть оно двумерно. По той же причине множество всех решений одного линейного уравнения в четырёхмерном пространстве Ax+By+Cz+Dt+E=0 само по себе трехмерно. Аналогично трехмерному случаю, вектор с координатами (A;B;C;D) перпендикулярен данной гиперплоскости и называется ее нормальным вектором.