Численные методы для уравнения Пуассона в цилиндрической системе координат

Уравнение Пуассона хорошо описывает физику некоторых процессов, происходящих в организме человека.
Последние достижения в изучении проблем электротомографии как альтернативного способа исследования тканей головного мозга сводятся к решению прямой и обратной задач для уравнения Пуассона, описывающего пространственное распределение потенциала.
Новые методы электротомографических исследований могут оказаться на несколько порядков экономичнее уже существующих (например, рентгенотомографии) и не требуют применения дорогостоящего оборудования.
Актуальность
Следующий слайд
Предыдущий слайд

Построение экономичных итерационных методов решения неоднородного уравнения Пуассона в цилиндрической системе координат для прямой задачи электроэнцефалографии.
Проверка эффективности построенных методов (скорость сходимости и количество вычислительных затрат) в работе на реальных моделях.
Цели и задачи
Следующий слайд
Предыдущий слайд

Следующий слайд
Предыдущий слайд
Объект исследования
Объектом исследования является цилиндр со встроенными электродами. Цилиндр заполняется солевым раствором (salt water) с электрической проводимостью 1.3 сименс/метр. В этот цилиндр могут помещаться физические тела с различной проводимостью. На два электрода подается ток и снимаются показания на других электродах.
-
+

Следующий слайд
Предыдущий слайд
Постановка задачи
Прямая задача может быть сформулирована следующим образом: по снятым на электродах значениям токов, геометрическим размерам и электрической проводимости исследуемого тела определить распределение потенциала по поверхности цилиндра.
Математически задача сводится к решению неоднородного уравнения Пуассона. В цилиндрических координатах оно запишется следующим образом:
На границе области задаются краевые условия Дирихле:

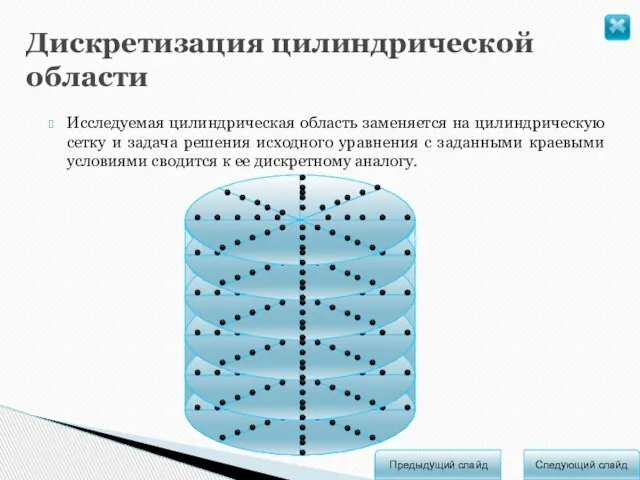
Следующий слайд
Предыдущий слайд
Дискретизация цилиндрической области
Исследуемая цилиндрическая область заменяется на цилиндрическую сетку и задача решения исходного уравнения с заданными краевыми условиями сводится к ее дискретному аналогу.

Следующий слайд
Предыдущий слайд
Упорядочение точек цилиндра
5
7
1
8
9
10
6
2
4
3
Упорядочение точек цилиндрической сетки происходит, как показано на рисунке. После заполнения самого нижнего слоя нумерация переносится на второй слой и т. д. вплоть до исчерпания всех слоев.

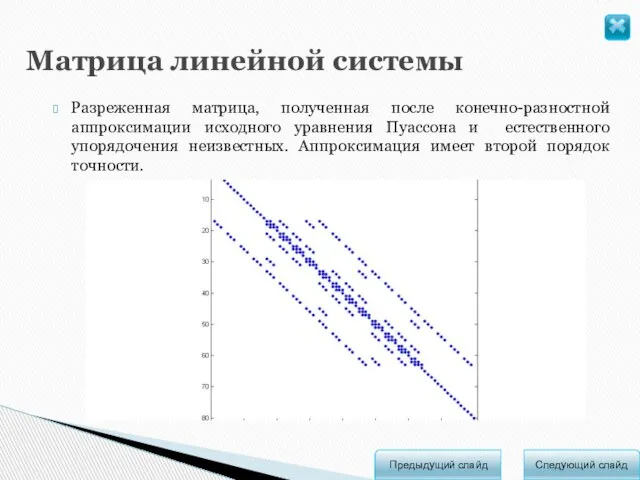
Следующий слайд
Предыдущий слайд
Матрица линейной системы
Разреженная матрица, полученная после конечно-разностной аппроксимации исходного уравнения Пуассона и естественного упорядочения неизвестных. Аппроксимация имеет второй порядок точности.

Решение линейной системы
Система линейных алгебраических уравнений
с разреженной матрицей решается методом бисопряженных градиентов. Для увеличения скорости сходимости строятся переобуславливатели Якоби и Фурье. Далее на работе модельной задачи сравниваются результаты с применением этих переобуславливателей .
Изначально предполагается, что решение системы методом бисопряженных градиентов с переобуславливателем Фурье требует меньшего числа итераций в сравнении работы этого же метода с переобуславливателем Якоби.
Следующий слайд
Предыдущий слайд

Основные результаты
Следующий слайд
Предыдущий слайд
Решение линейной системы для модельной задачи на сетке
с помощью встроенной в Matlab 8.0 функции bicg с переобуславливателем Фурье требует 34 итерации для точности .
Задача тестировалась и для других сеток. Число итераций практически не зависит от размерности сетки, что дает основание на то, что тестируемый солвер достаточно эффективен для сеток с большим числом узлов.

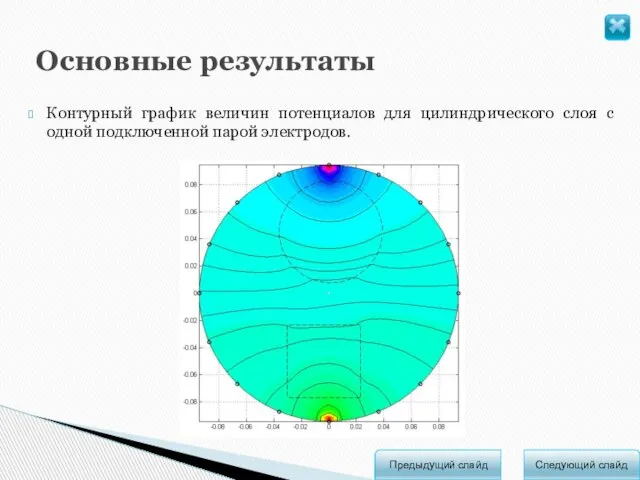
Основные результаты
Контурный график величин потенциалов для цилиндрического слоя с одной подключенной парой электродов.
Следующий слайд
Предыдущий слайд

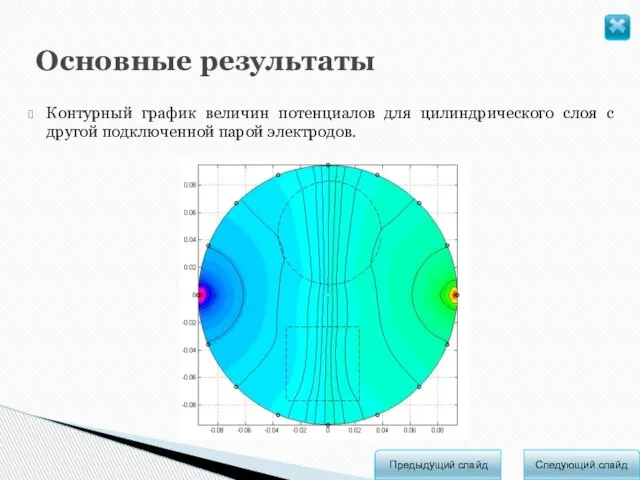
Основные результаты
Следующий слайд
Предыдущий слайд
Контурный график величин потенциалов для цилиндрического слоя с другой подключенной парой электродов.

Построение новых быстрых итерационных методов решения неоднородного уравнения Пуассона, как-то метод бисопряженных градиентов с переобуславливателем Фурье, может иметь прикладное применение в медицине, в частности поможет решать обратную задачу электроэнцефалографии, состоящую из многократного решения прямой задачи.
Научная новизна
Следующий слайд
Предыдущий слайд

Неоднородное уравнение Пуассона в цилиндрической системе координат.
Матрицы линейных систем для прямой модельной задачи.
Метод бисопряженных градиентов с переобуславливателем Фурье для решения прямой модельной задачи.
Эффективность исследуемого метода.
Основные положения, выносимые на защиту
Следующий слайд
Предыдущий слайд