Слайд 2R = 1 (радиус)
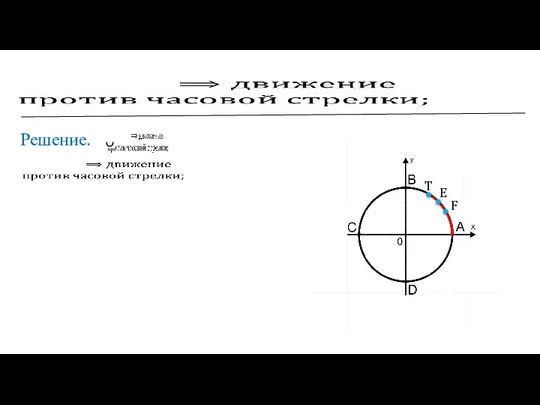
АВ — I четверть,
BC — II четверть,
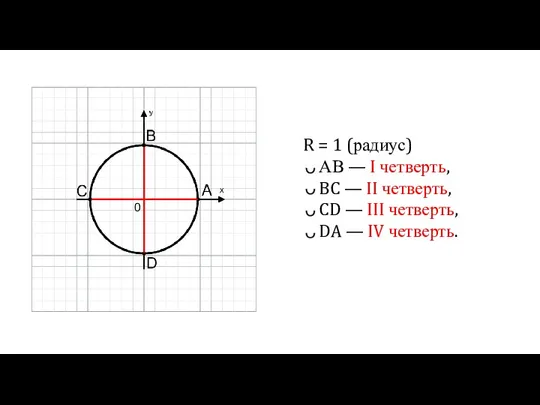
CD — III четверть,
DA — IV четверть.
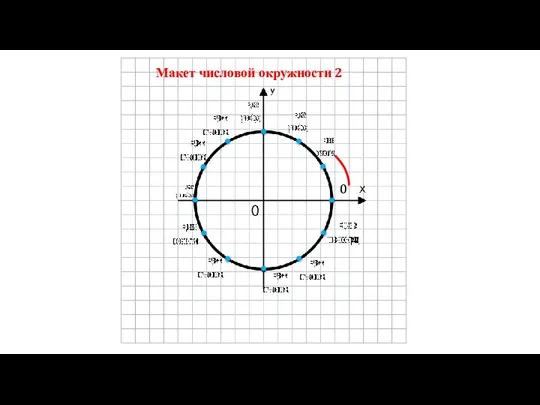
Слайд 3Единичная окружность.
Точка А – начало отсчёта.

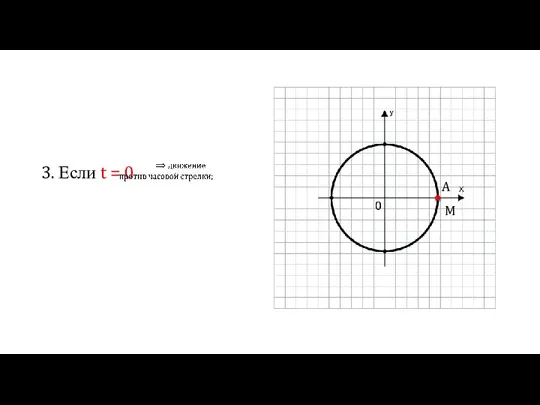
Слайд 41. Если t > 0
Если от точки А перемещаемся
в положительном направлении
(против
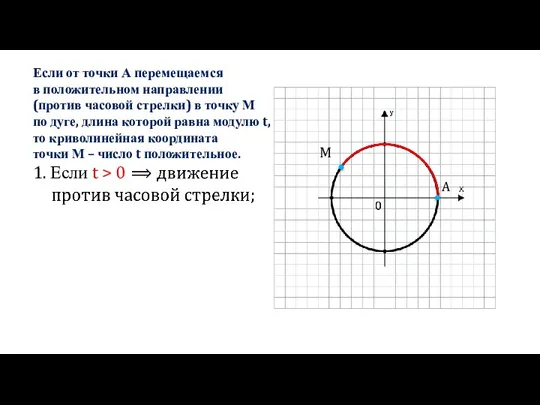
часовой стрелки) в точку М
по дуге, длина которой равна модулю t,
то криволинейная координата
точки М – число t положительное.
Слайд 52. Если t < 0
Если от точки А перемещаемся
по дуге по часовой

стрелке (отрицательное направление)
на расстояние модуль t, то криволинейная координата
Точки М – число t отрицательное.
Слайд 7Единичная окружность с установленным соответствием (между действительными числами и точками окружности) —

числовая окружность.
Слайд 8 l – длина окружности.
l = 2πR, где π ≈

3,14;
R – радиус окружности.
R = 1, значит l = 2π ≈ 6,28.
Слайд 9Пример 1. Найти на числовой окружности точку,
которая соответствует заданному числу:
Решение.
(Так обозначаем
криволинейные
координаты
точек).

Слайд 11
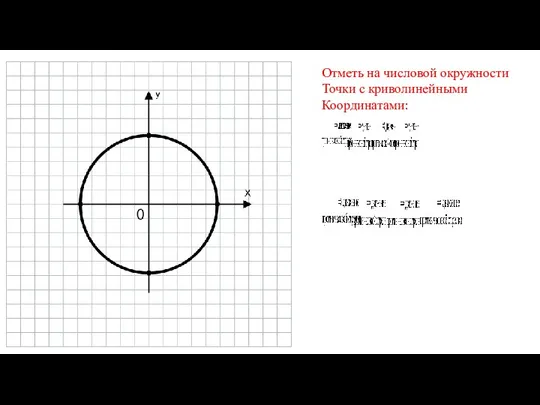
Отметь на числовой окружности
Точки с криволинейными
Координатами:
Слайд 14
0
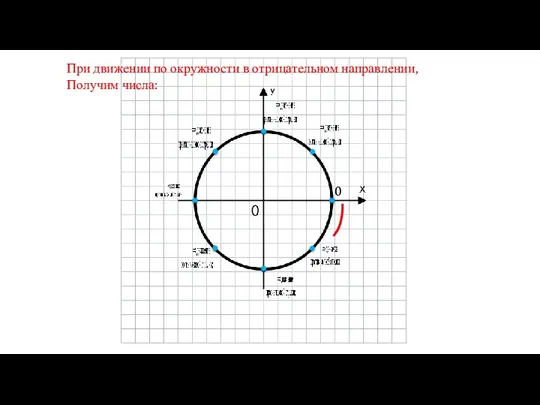
При движении по окружности в отрицательном направлении,
Получим числа:
Слайд 15Пример 4. Найти на числовой окружности точки, соответствующие числу 1.
Решение.
? ≈ 3,14;
1
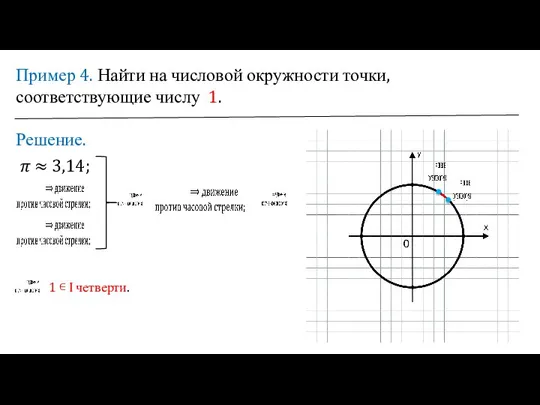
∊ I четверти.
Слайд 16Если точка М числовой окружности соответствуют числу t, то она соответствует и

любому числу вида t + 2πk, где k ϵ Z.












 Tesla
Tesla Оригами новогодняя ёлка
Оригами новогодняя ёлка Презентация на тему Решение задач по теме Колебания и волны
Презентация на тему Решение задач по теме Колебания и волны  Budowa roślin
Budowa roślin Презентация на тему Россия при Петре I
Презентация на тему Россия при Петре I  Пакетные предложения. Разработан для хоккея спроектирован для детей. Окно №2
Пакетные предложения. Разработан для хоккея спроектирован для детей. Окно №2 Презентация на тему Как сочинить волшебную сказку
Презентация на тему Как сочинить волшебную сказку  Развитие магистральных сетей: задачи энергостроительного комплекса
Развитие магистральных сетей: задачи энергостроительного комплекса Решение задач. Идеальный газ
Решение задач. Идеальный газ Непривычная динамика ценна рынке жилья:впервые за 20 летАналитический центр w w w . I R N . r u Март 2011 г.
Непривычная динамика ценна рынке жилья:впервые за 20 летАналитический центр w w w . I R N . r u Март 2011 г. o Центр корпоративного обучения « Оксфорд Класс » создан в 2007 г. в партнерстве с языковой школой Оксфорд Класс, г. Киев,Украина, год о
o Центр корпоративного обучения « Оксфорд Класс » создан в 2007 г. в партнерстве с языковой школой Оксфорд Класс, г. Киев,Украина, год о Скульптура АНТИЧНОСТИ
Скульптура АНТИЧНОСТИ Сервировка сладкого стола. Праздничный этикет
Сервировка сладкого стола. Праздничный этикет Чтобы зубы были здоровыми
Чтобы зубы были здоровыми Тема занятия: «Учет кассовых операций»
Тема занятия: «Учет кассовых операций» Требования к современному уроку
Требования к современному уроку Научно-методическое обеспечение деятельности школьных библиотекарей
Научно-методическое обеспечение деятельности школьных библиотекарей Муниципальное бюджетное общеобразовательное учреждение гимназия № 52 Октябрьского района города Росто
Муниципальное бюджетное общеобразовательное учреждение гимназия № 52 Октябрьского района города Росто России первая любовь
России первая любовь Графические интерфейсыпакет Tkinter
Графические интерфейсыпакет Tkinter Презентация на тему Мир
Презентация на тему Мир Операции с грузами по прибытию на станцию назначения
Операции с грузами по прибытию на станцию назначения Презентация на тему Познавательные процессы 8 класс
Презентация на тему Познавательные процессы 8 класс Русская народная музыка
Русская народная музыка Портрет первоклассника
Портрет первоклассника Организация структуры базы данных
Организация структуры базы данных Теория обучения в информационном обществе
Теория обучения в информационном обществе Особенности правового режима использования олимпийской и паралимпийской символики
Особенности правового режима использования олимпийской и паралимпийской символики