Содержание
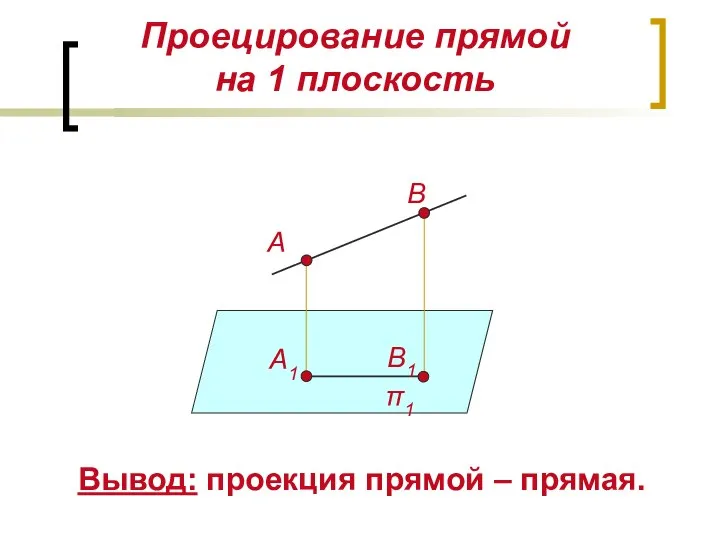
- 2. Проецирование прямой на 1 плоскость Вывод: проекция прямой – прямая. А А1 π1 В В1
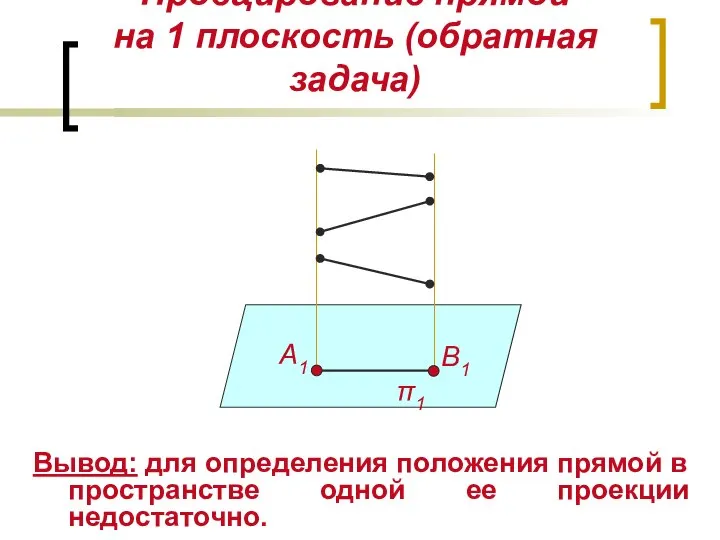
- 3. Проецирование прямой на 1 плоскость (обратная задача) Вывод: для определения положения прямой в пространстве одной ее
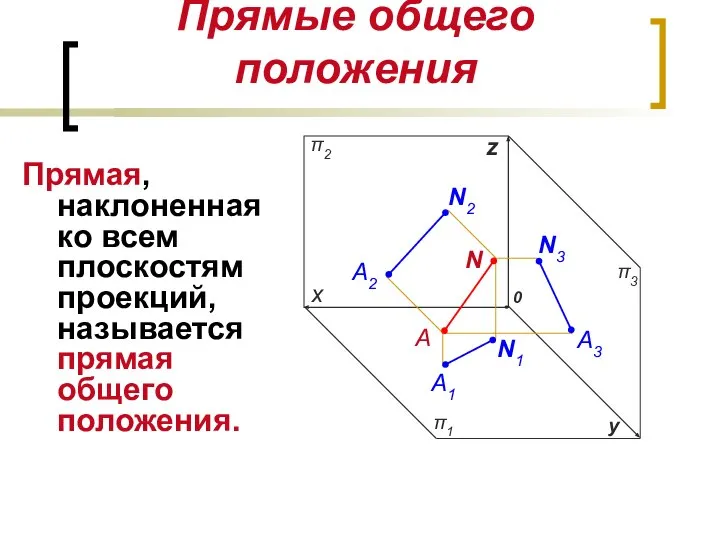
- 4. Прямые общего положения Прямая, наклоненная ко всем плоскостям проекций, называется прямая общего положения. π1 π3 А1
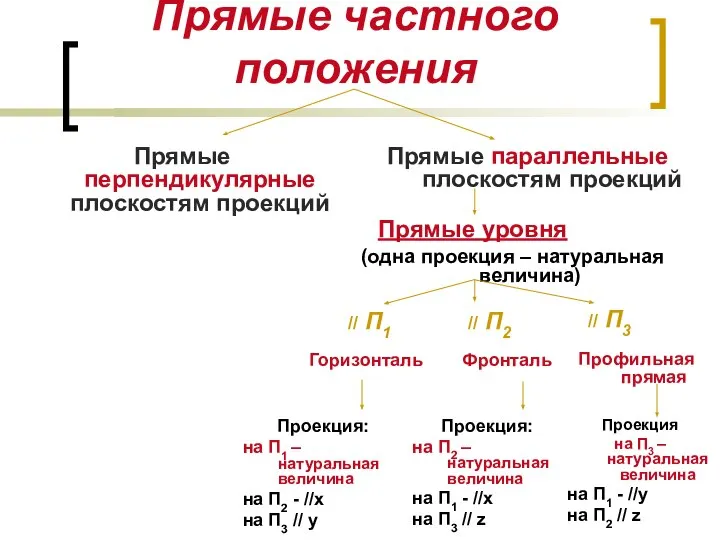
- 5. Прямые частного положения Прямые перпендикулярные плоскостям проекций Прямые параллельные плоскостям проекций Проецирующие прямые (одна проекция есть
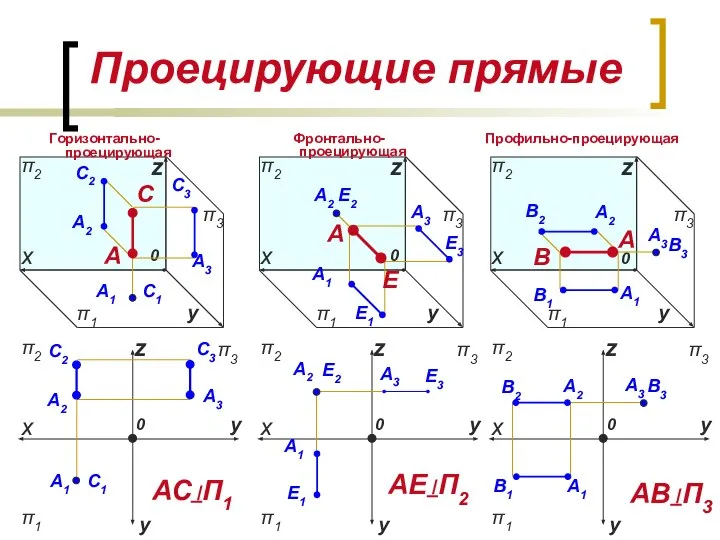
- 6. Проецирующие прямые π3 у 0 z х π2 π2 z х π1 π1 π3 у у
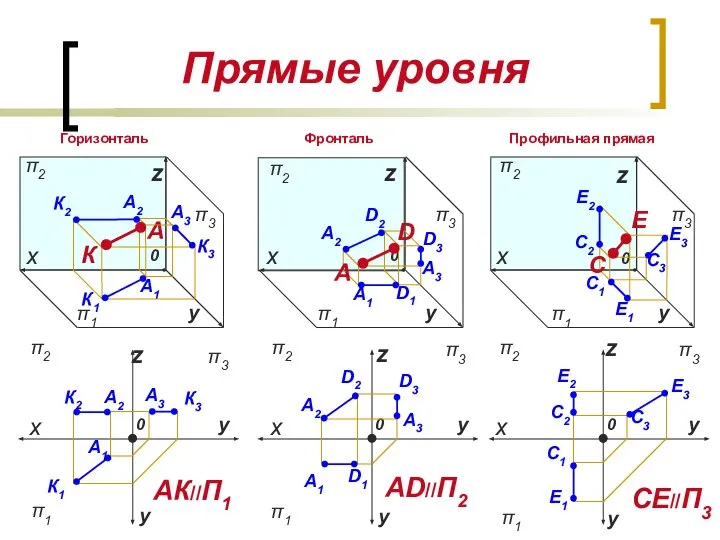
- 7. Прямые частного положения Прямые перпендикулярные плоскостям проекций Прямые параллельные плоскостям проекций Прямые уровня (одна проекция –
- 8. Прямые уровня π3 у 0 z х π2 π2 z х π1 π1 π3 у у
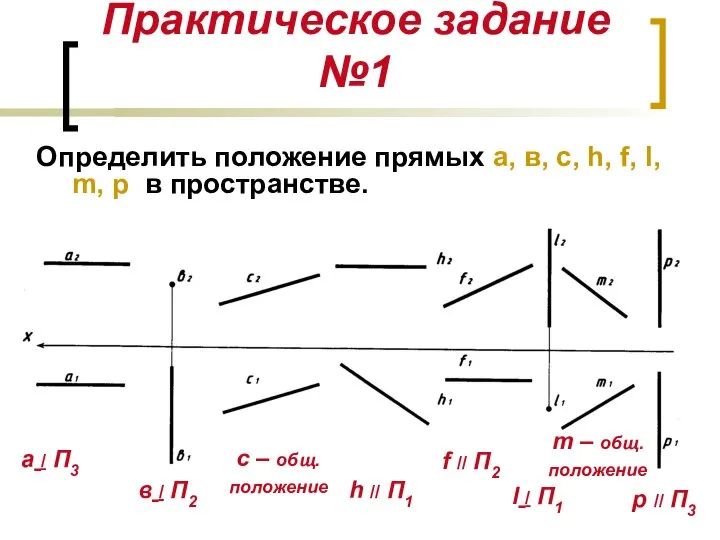
- 9. Практическое задание №1 Определить положение прямых а, в, с, h, f, l, m, p в пространстве.
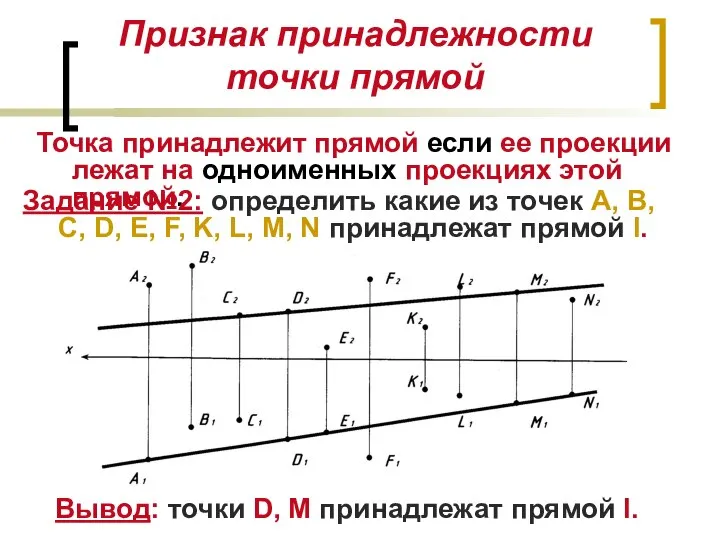
- 10. Признак принадлежности точки прямой Точка принадлежит прямой если ее проекции лежат на одноименных проекциях этой прямой.
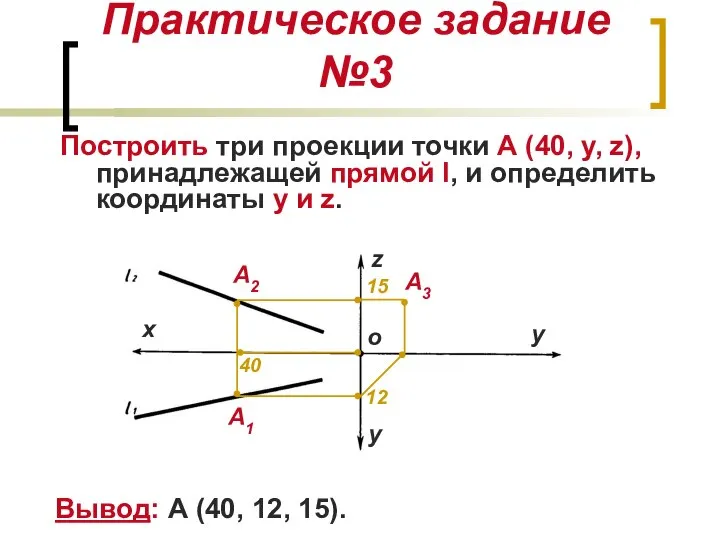
- 11. Практическое задание №3 Построить три проекции точки А (40, y, z), принадлежащей прямой l, и определить
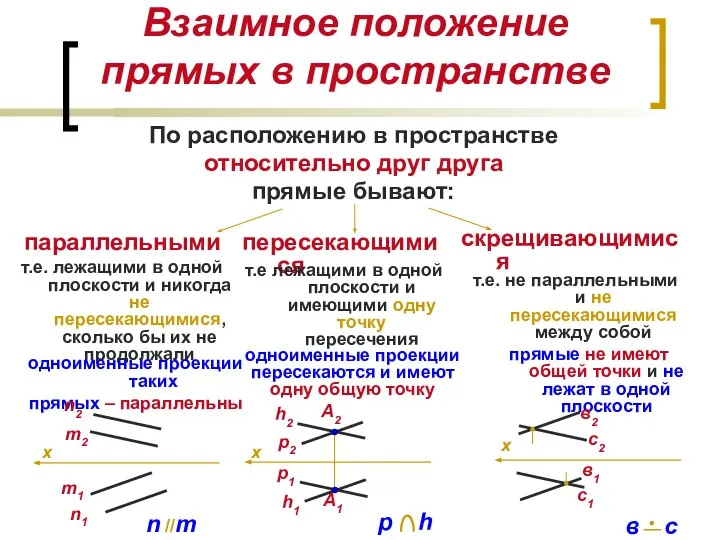
- 12. Взаимное положение прямых в пространстве параллельными скрещивающимися По расположению в пространстве относительно друг друга прямые бывают:
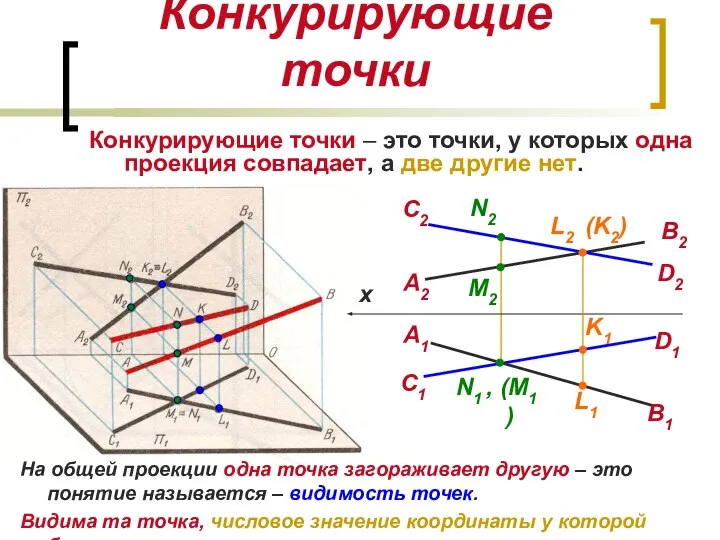
- 13. Конкурирующие точки Конкурирующие точки – это точки, у которых одна проекция совпадает, а две другие нет.
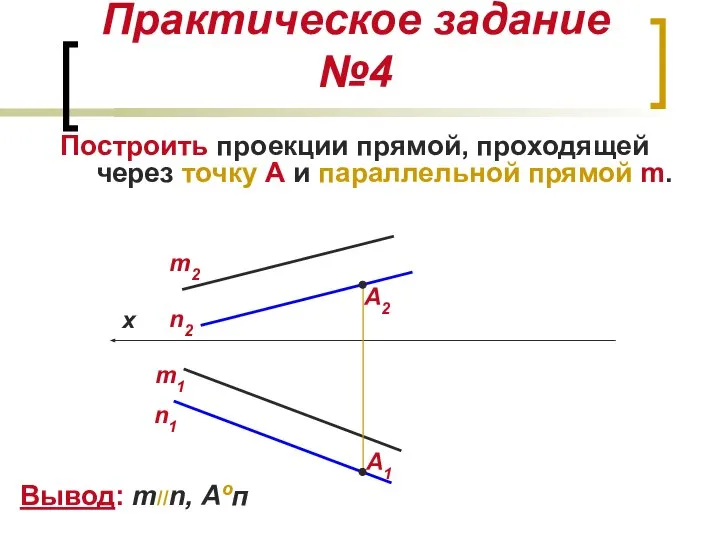
- 14. Практическое задание №4 Построить проекции прямой, проходящей через точку А и параллельной прямой m. А2 х
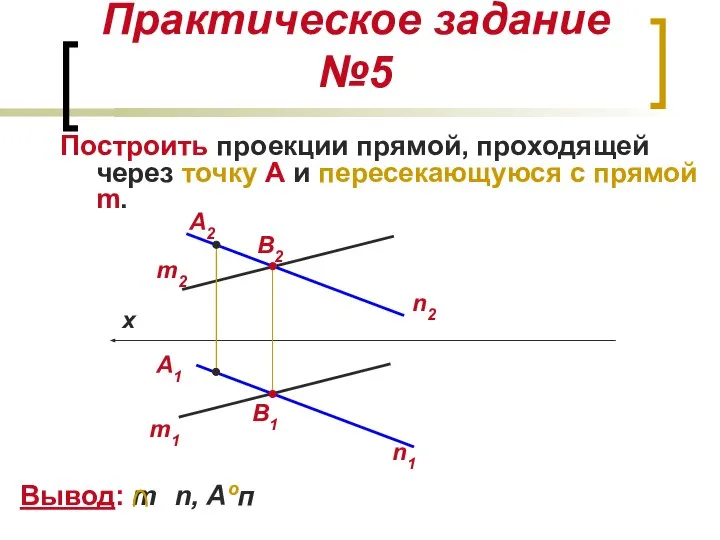
- 15. Практическое задание №5 Построить проекции прямой, проходящей через точку А и пересекающуюся с прямой m. А2
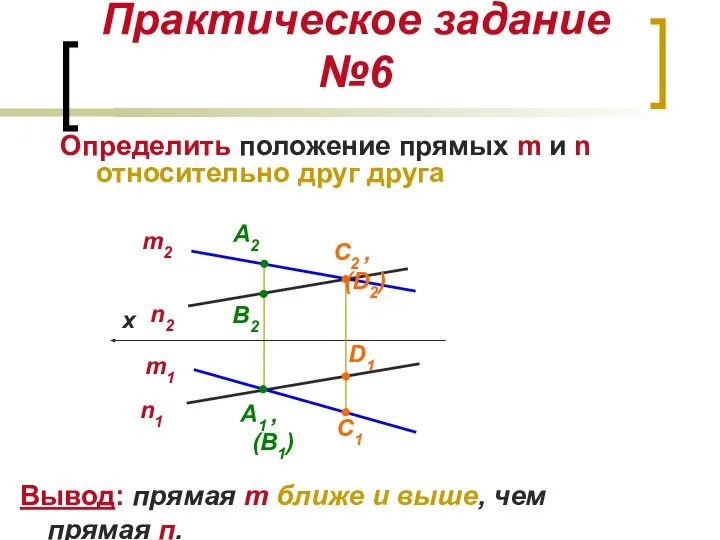
- 16. Практическое задание №6 Определить положение прямых m и n относительно друг друга А2 х А1 ,
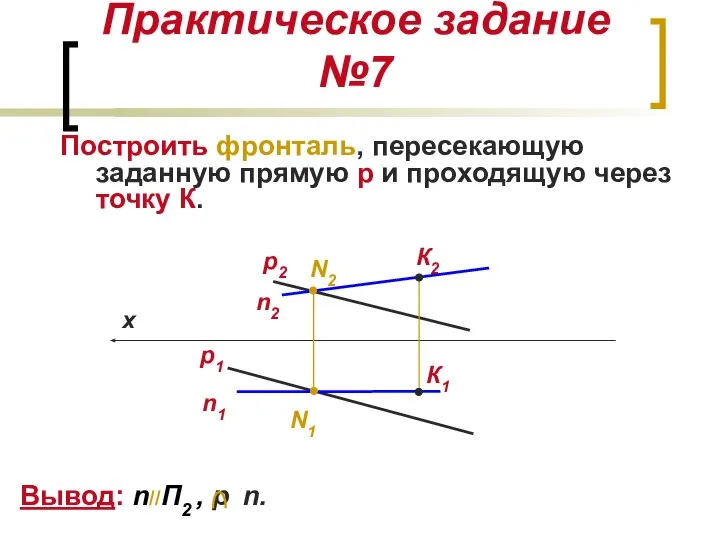
- 17. Практическое задание №7 Построить фронталь, пересекающую заданную прямую р и проходящую через точку К. К2 х
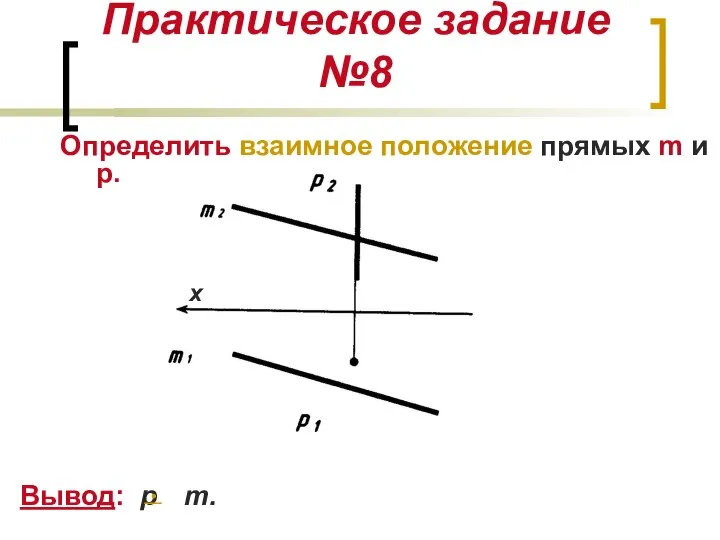
- 18. Практическое задание №8 Определить взаимное положение прямых m и р. Вывод: р m. х
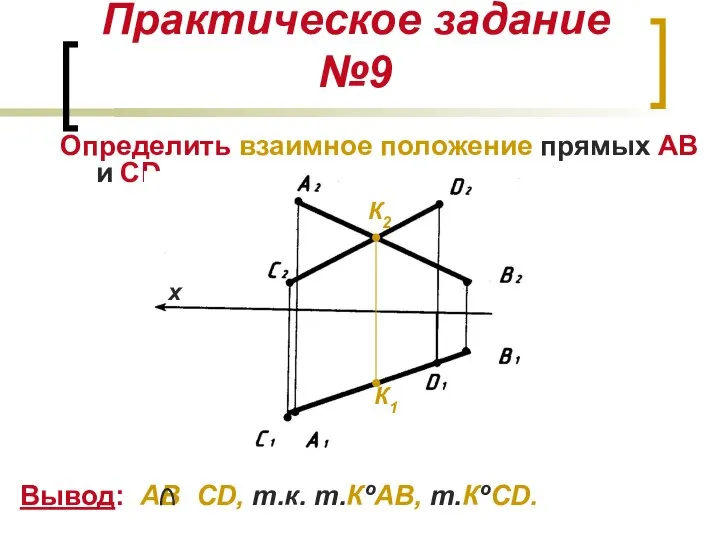
- 19. Практическое задание №9 Определить взаимное положение прямых АВ и CD. Вывод: АВ CD, т.к. т.КºАВ, т.КºCD.
- 21. Скачать презентацию

 ДЦП
ДЦП  Презентация на тему Лишайники, водоросли, мхи
Презентация на тему Лишайники, водоросли, мхи Тактика поведения в сложных ситуациях взаимодействия
Тактика поведения в сложных ситуациях взаимодействия Драма как род литературы
Драма как род литературы Презентация на тему Раскрытие скобок
Презентация на тему Раскрытие скобок  RTV 133
RTV 133 Болезни зубов
Болезни зубов Развитие орфографической зоркости у младших школьников
Развитие орфографической зоркости у младших школьников Презентация на тему Синергетика
Презентация на тему Синергетика  Черное и белое духовенство
Черное и белое духовенство Теории происхождения права
Теории происхождения права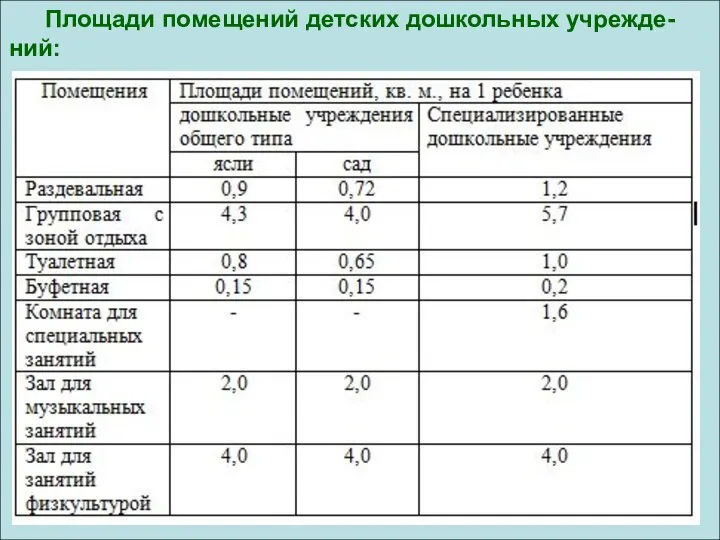 Площади помещений детских дошкольных учреждений
Площади помещений детских дошкольных учреждений Характеристика перцептивной стороны общения
Характеристика перцептивной стороны общения 1-й квест
1-й квест Курс CMS Wordpress. Практика. Выбор тематики своего сайта
Курс CMS Wordpress. Практика. Выбор тематики своего сайта Подростковые и молодежные субкультуры XXI века
Подростковые и молодежные субкультуры XXI века Мини-музей "Югра"
Мини-музей "Югра" Исследовательская краеведческая работа ученика 11 «А» класса Андреевской СОШ Судогодского района Владимирской области Воронин
Исследовательская краеведческая работа ученика 11 «А» класса Андреевской СОШ Судогодского района Владимирской области Воронин Методика Масару Ибука
Методика Масару Ибука Структура современного урока. Роль мотивации и рефлексии в учебном процессе
Структура современного урока. Роль мотивации и рефлексии в учебном процессе Как оформить инвестиции: от простого к сложному
Как оформить инвестиции: от простого к сложному Использование национально-регионального компонента в обучении химии на элективных курсах
Использование национально-регионального компонента в обучении химии на элективных курсах Дистанция в заданном направлении
Дистанция в заданном направлении Животные долгожители
Животные долгожители Здравствуй, Зимушка-Зима!
Здравствуй, Зимушка-Зима! Методы генной инженерии
Методы генной инженерии ВИРТУАЛЬНАЯ ЛЕКСИКОГРАФИЧЕСКАЯ ЛАБОРАТОРИЯ ДЛЯ ТОЛКОВЫХ СЛОВАРЕЙ VIRTUAL LEXICOGRAPHICAL LABORATORY FOR EXPLANATORY DICTIONARIES Остапова И. В. (
ВИРТУАЛЬНАЯ ЛЕКСИКОГРАФИЧЕСКАЯ ЛАБОРАТОРИЯ ДЛЯ ТОЛКОВЫХ СЛОВАРЕЙ VIRTUAL LEXICOGRAPHICAL LABORATORY FOR EXPLANATORY DICTIONARIES Остапова И. В. ( Технология проблемного обучения на уроках русского языка
Технология проблемного обучения на уроках русского языка