Complex plasmas

Plasmas span a tremendous range of temperatures and densities – from the low densities observed in the ionosphere or in space plasmas to the huge densities in the core of white dwarf stars. Plasmas exist at even higher densities (such as in the interior of neutron stars or in heavy ion collision experiments) where nuclei and nucleons break up giving rise to the quark-gluon plasma.
Plasma physics has always produced results that reached out into other fields. Examples are the explanation of the collective oscillations of the electron gas in metals or of the electron-hole plasma in semiconductors, e.g. A similar development occurs now in nonideal plasmas.

Self-organized filaments in
dielectric barrier discharges

What is DBD?
Dielectric-barrier discharge (DBD) is the electrical discharge between two electrodes separated by an insulating dielectric barrier. Originally called silent (inaudible) discharge and also known as ozone production discharge or partial discharge, it was first reported by Ernst Werner von Siemens in 1857.

Dielectric barrier discharges are widely used in industrial application due to their ability to produce large volume non-equilibrium plasmas at high pressure.

when the radial diffusion length of one electron during its transit from cathode to anode become small with respect to the transverse dimension of the discharge one can expect that a large volume non-thermal plasma will exhibit strong radial non-uniformities.
A wide range of morphogenesis features can be obtained, from complex stationary patterns, to the generation, annihilation and traveling of dissipative solitons and pseudo-molecules

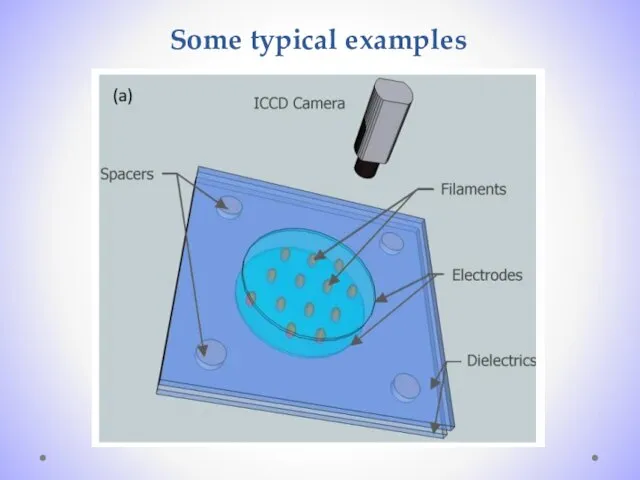
Some typical examples

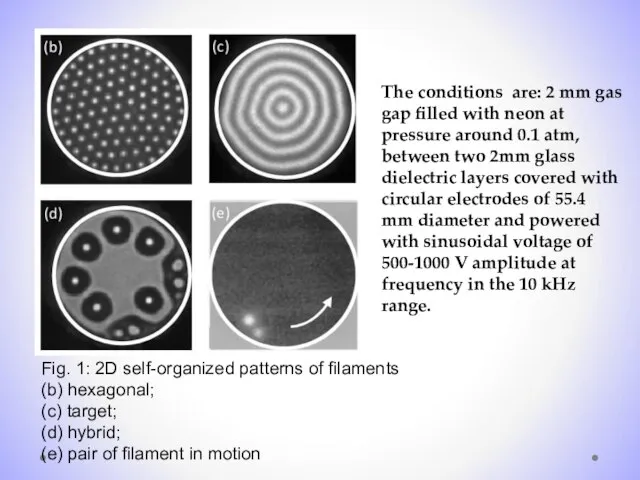
Fig. 1: 2D self-organized patterns of filaments
(b) hexagonal;
(c) target;
(d) hybrid;
(e) pair of filament in motion
The conditions are: 2 mm gas gap filled with neon at pressure around 0.1 atm, between two 2mm glass dielectric layers covered with circular electrodes of 55.4
mm diameter and powered with sinusoidal voltage of 500-1000 V amplitude at frequency in the 10 kHz range.

Experiment carried by
They used two different systems, a two dimensional geometry shown in figure 1a and a one dimensional geometry, displayed in figure 2a.
Fig. 2:

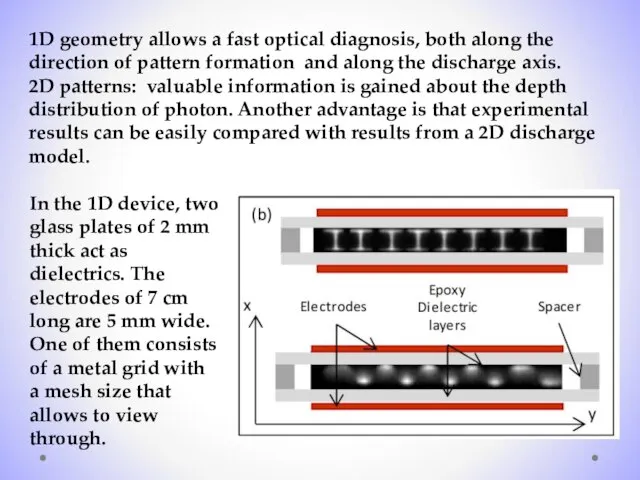
1D geometry allows a fast optical diagnosis, both along the direction of pattern formation and along the discharge axis.
2D patterns: valuable information is gained about the depth distribution of photon. Another advantage is that experimental results can be easily compared with results from a 2D discharge model.
In the 1D device, two glass plates of 2 mm thick act as dielectrics. The electrodes of 7 cm long are 5 mm wide.
One of them consists of a metal grid with a mesh size that allows to view through.

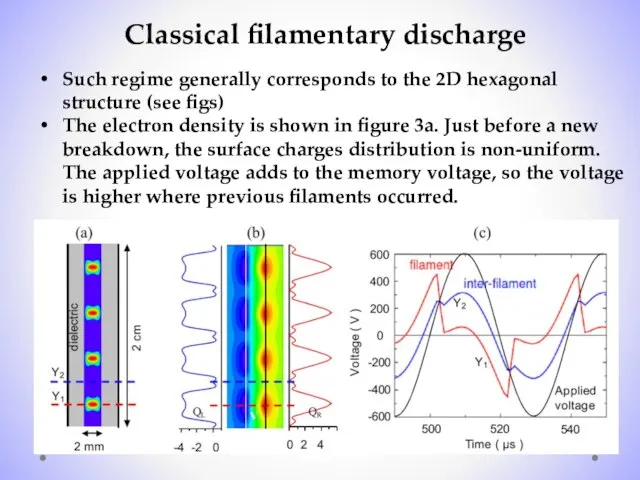
Classical filamentary discharge
Such regime generally corresponds to the 2D hexagonal structure (see figs)
The electron density is shown in figure 3a. Just before a new breakdown, the surface charges distribution is non-uniform. The applied voltage adds to the memory voltage, so the voltage is higher where previous filaments occurred.

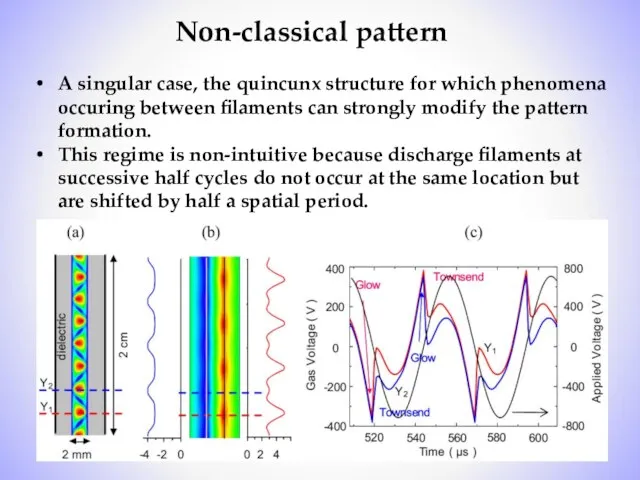
Non-classical pattern
A singular case, the quincunx structure for which phenomena occuring between filaments can strongly modify the pattern formation.
This regime is non-intuitive because discharge filaments at successive half cycles do not occur at the same location but are shifted by half a spatial period.

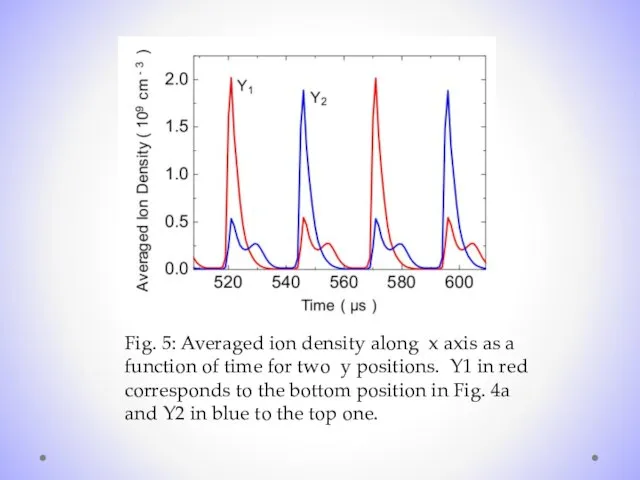
Fig. 5: Averaged ion density along x axis as a function of time for two y positions. Y1 in red corresponds to the bottom position in Fig. 4a and Y2 in blue to the top one.

surface charges distributions on both dielectric sides are distributed much more uniformly compared to the classical structure. The memory effect of surface charges will be less likely to promote the breakdown at a specific location.
Another parameter will then compete with surface memory charges, it is the volume memory charges.
Under some conditions, once the filamentary regime ended or during its extinction, the voltage across the gas between two filaments is large enough (see figure 4c at t = 530 µs) to generate a Townsend type discharge.

The large variety of pattern filaments that can be observed in DBDs is the result of strongly non-linear activator-inhibitor mechanisms and it is difficult to present a simple theory that can predict this variety.
Nevertheless there have been highlighted the competition between surface charges and volume charges to decide the location of breakdown. Volume charges just before breakdown and distribution of surface charges are strongly related to the presence of a secondary Townsend discharge occurring during the same half-period that the glow discharge.
The occurence of this discharge is also responsible for soliton dynamics and can generate merging or separation of filaments.

Modeling carried by
The presence and/or the consequences of bifurcations have been encountered the modeling of DC glow microdischarges even in apparently simple situations.
These bifurcations are a consequence of the existence of multiple solutions in the theory of basic DC glow discharges.

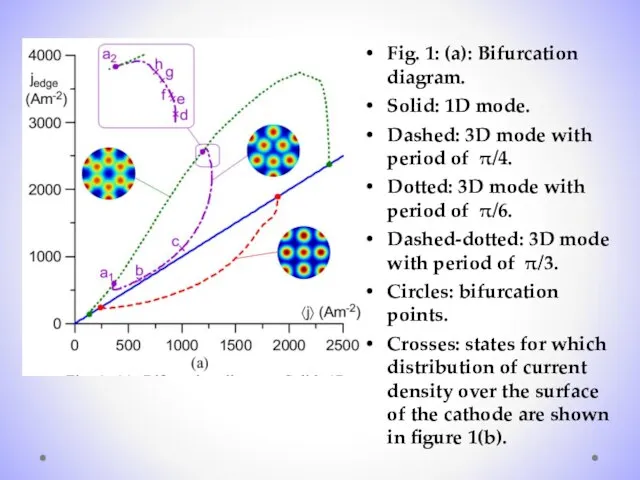
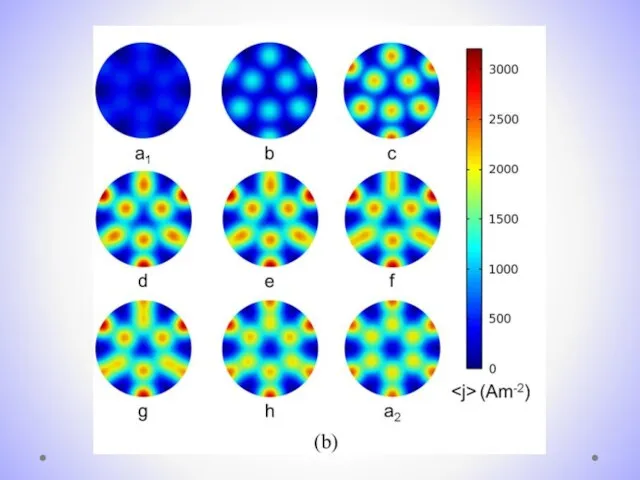
Fig. 1: (a): Bifurcation diagram.
Solid: 1D mode.
Dashed: 3D mode with period of π/4.
Dotted: 3D mode with period of π/6.
Dashed-dotted: 3D mode with period of π/3.
Circles: bifurcation points.
Crosses: states for which distribution of current density over the surface of the cathode are shown in figure 1(b).