Содержание
- 2. What is important in the representation of a crystal ?
- 3. What is important in the representation of a crystal ? It is not its shape It
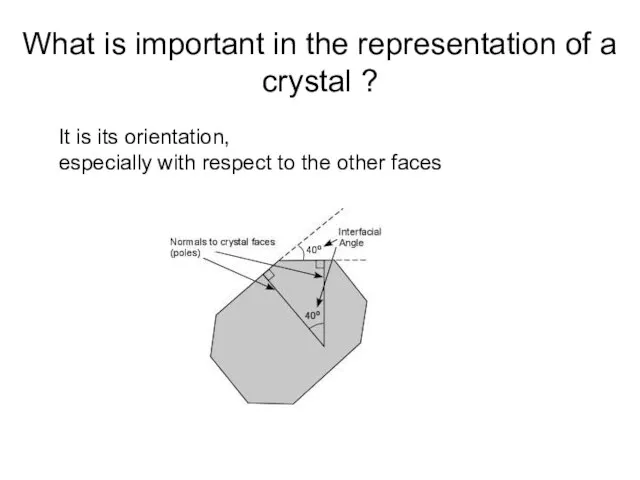
- 4. What is important in the representation of a crystal ? It is its orientation, especially with
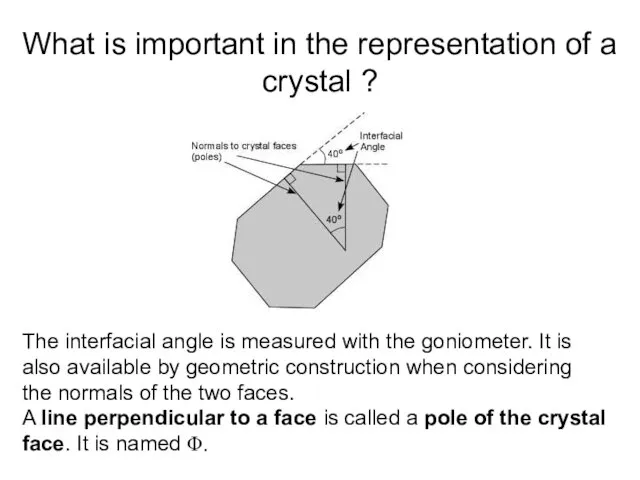
- 5. What is important in the representation of a crystal ? The interfacial angle is measured with
- 6. How to flatten the Earth ? Illustration by Rubens for "Opticorum libri sex philosophis juxta ac
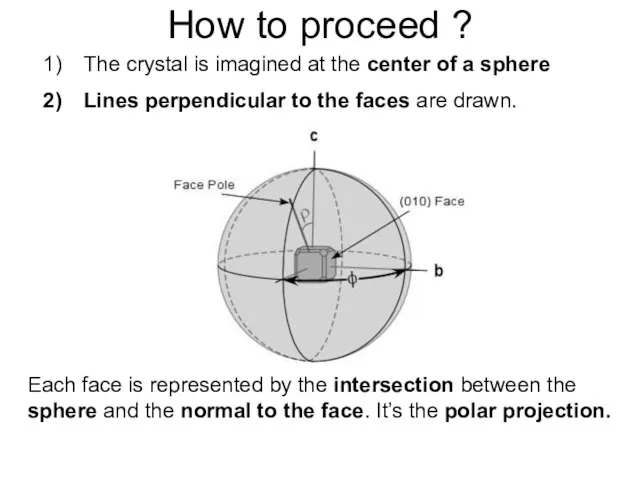
- 7. How to proceed ? The crystal is imagined at the center of a sphere Lines perpendicular
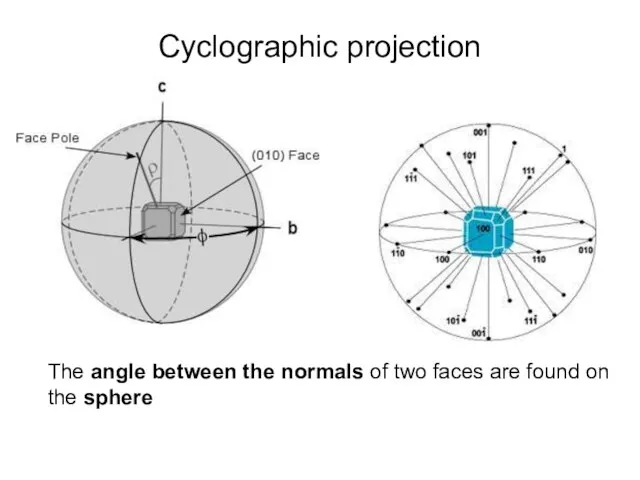
- 8. Cyclographic projection The angle between the normals of two faces are found on the sphere
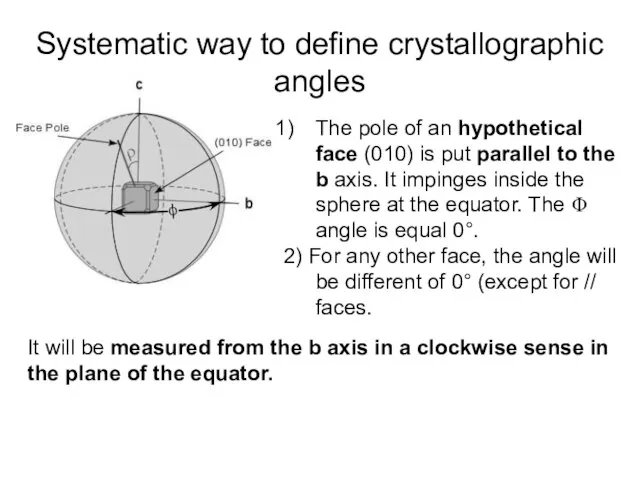
- 9. Systematic way to define crystallographic angles The pole of an hypothetical face (010) is put parallel
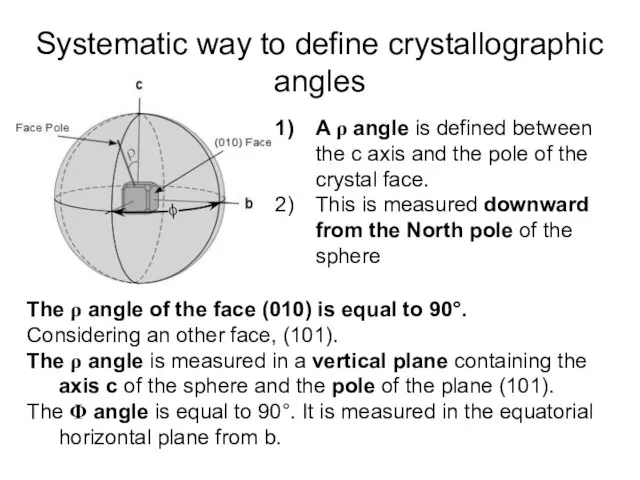
- 10. Systematic way to define crystallographic angles A ρ angle is defined between the c axis and
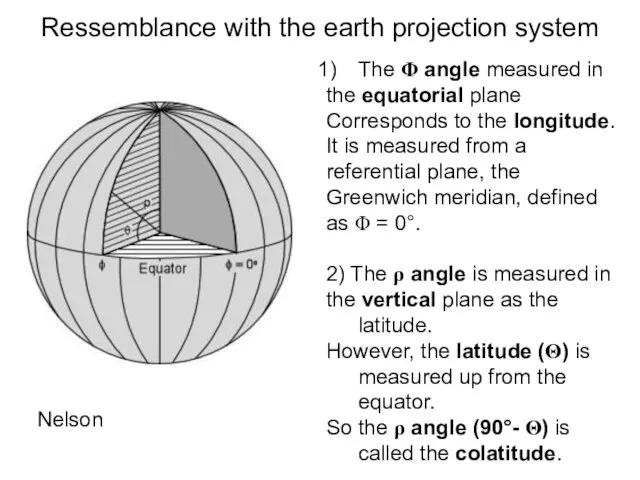
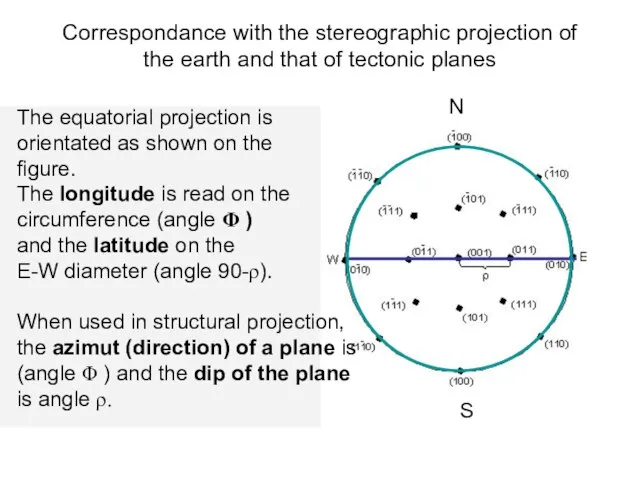
- 11. Ressemblance with the earth projection system Nelson The Φ angle measured in the equatorial plane Corresponds
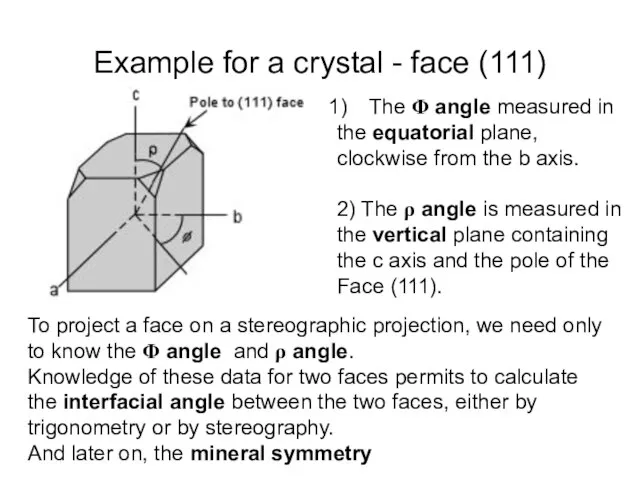
- 12. Example for a crystal - face (111) The Φ angle measured in the equatorial plane, clockwise
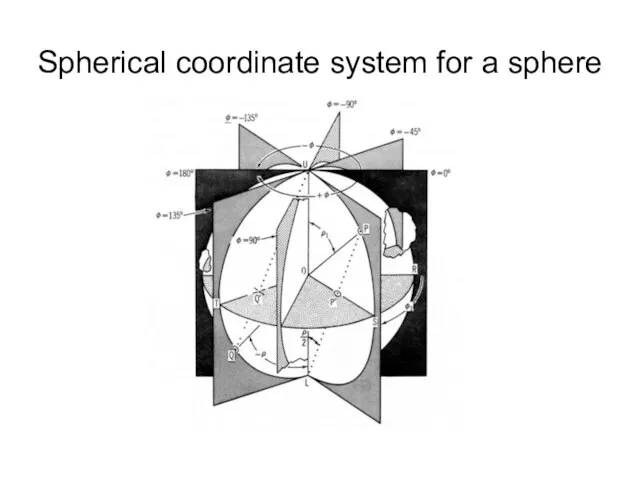
- 13. Spherical coordinate system for a sphere
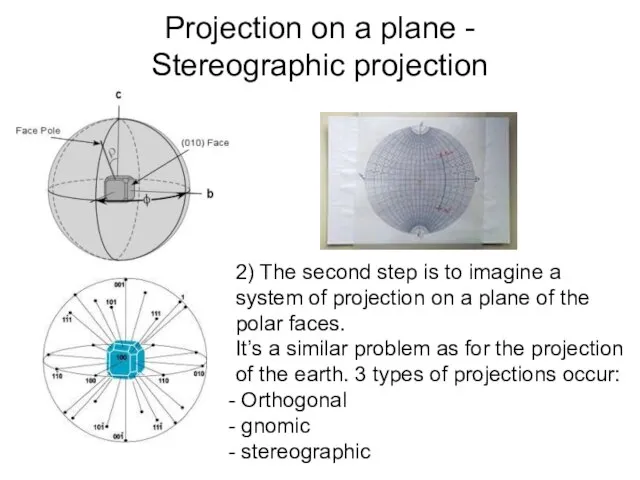
- 14. Projection on a plane - Stereographic projection 2) The second step is to imagine a system
- 15. Why to use a stereographic projection in crystallography?
- 16. Why to use a stereographic projection in crystallography? The projection of a circle is maintained as
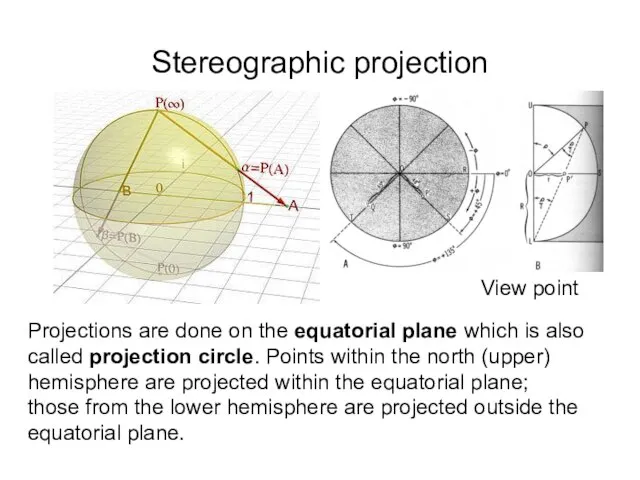
- 17. Stereographic projection Projections are done on the equatorial plane which is also called projection circle. Points
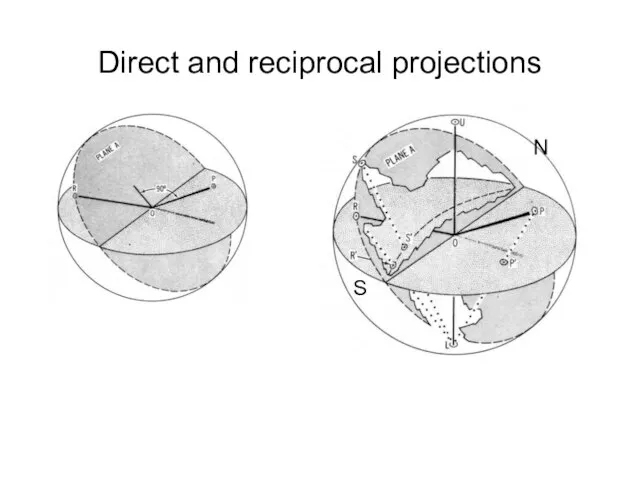
- 18. Direct and reciprocal projections N S
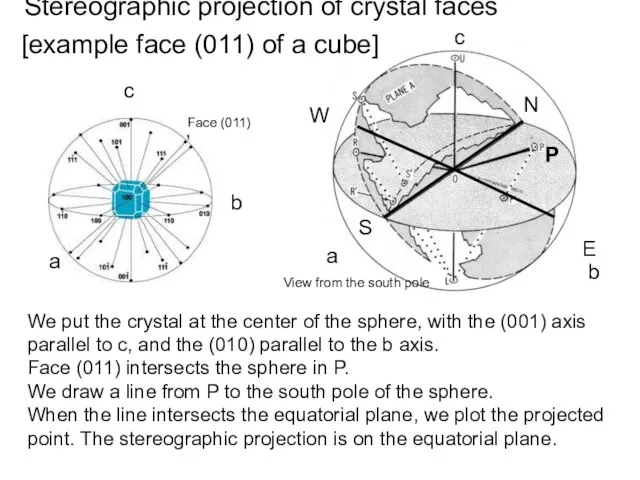
- 19. Stereographic projection of crystal faces c b a View from the south pole [example face (011)
- 20. Stereographic projection of crystal faces [example face (011) of a cube]
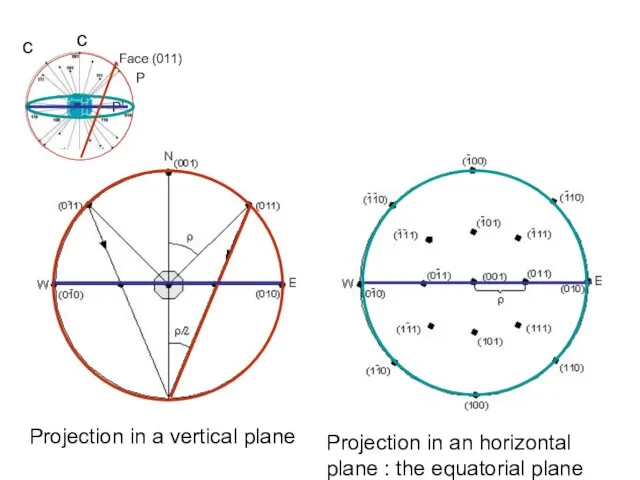
- 21. c Projection in a vertical plane Projection in an horizontal plane : the equatorial plane
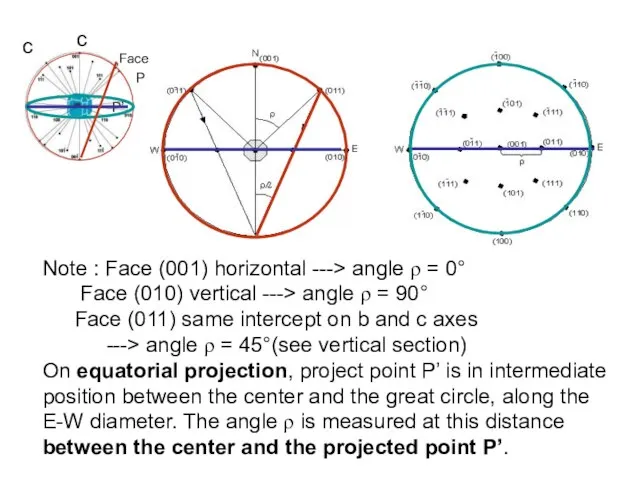
- 22. c Note : Face (001) horizontal ---> angle ρ = 0° Face (010) vertical ---> angle
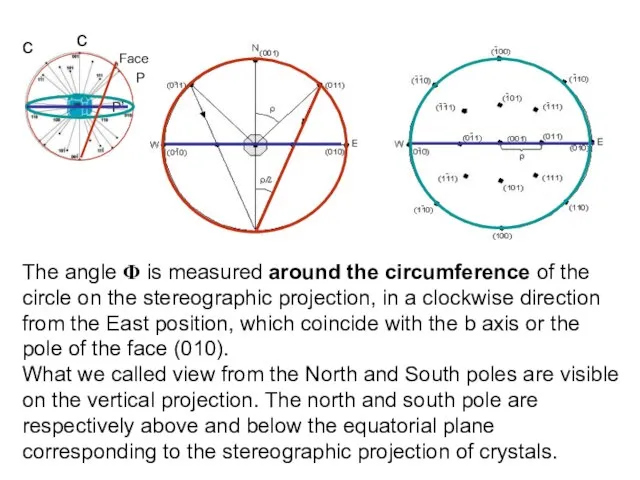
- 23. c The angle Φ is measured around the circumference of the circle on the stereographic projection,
- 24. Correspondance with the stereographic projection of the earth and that of tectonic planes
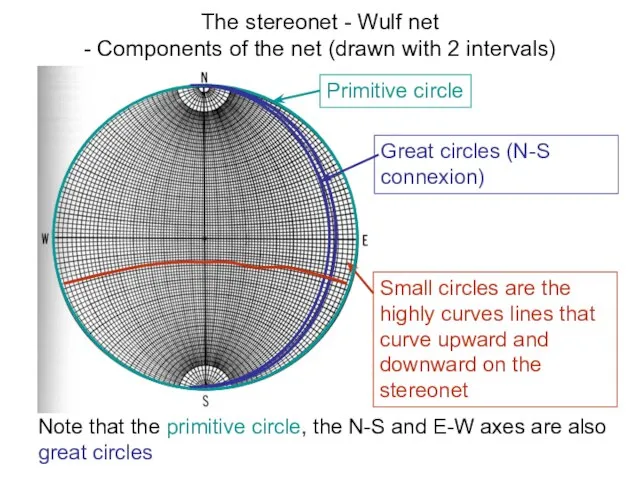
- 25. The stereonet - Wulf net - Components of the net (drawn with 2 intervals) Primitive circle
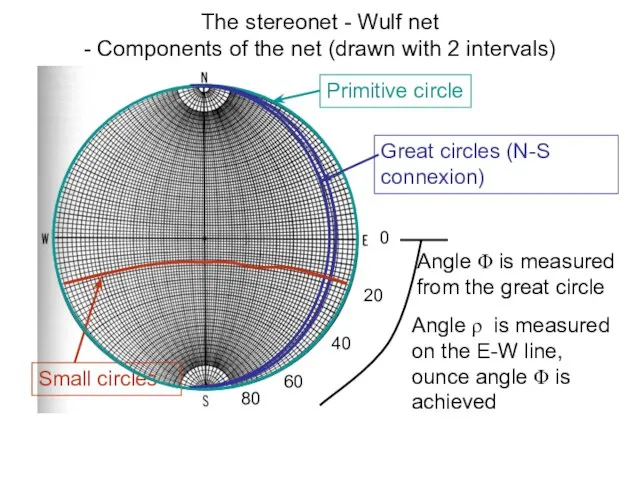
- 26. The stereonet - Wulf net - Components of the net (drawn with 2 intervals) Primitive circle
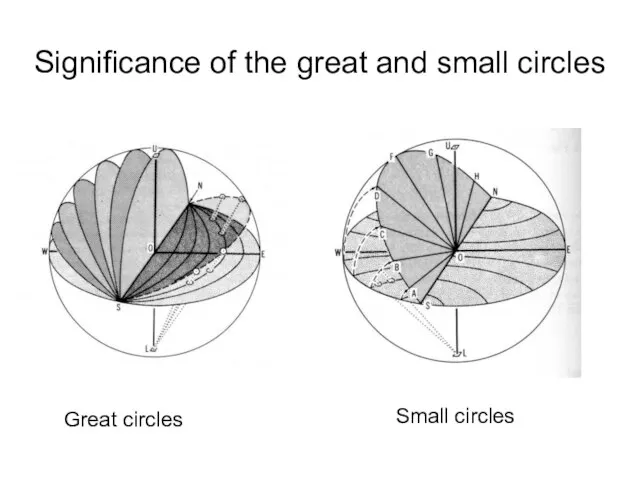
- 27. Significance of the great and small circles Great circles Small circles
- 28. Use of the stereonet - (1) All crystal faces are plotted as poles (lines perpendicular to
- 29. Use of the stereonet - practical uses (2) To plot a face: First measure the value
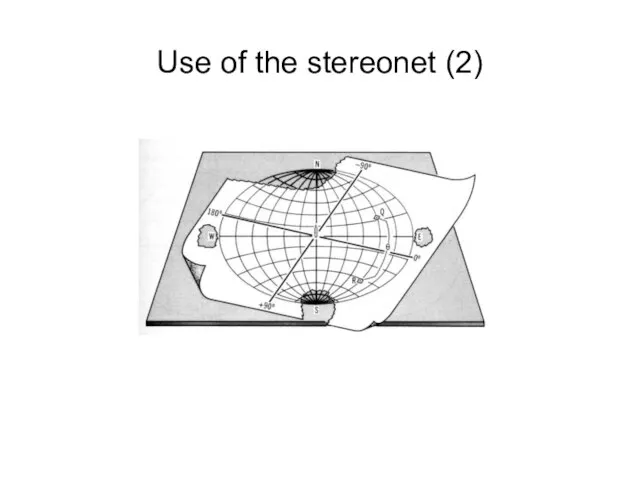
- 30. Use of the stereonet (2)
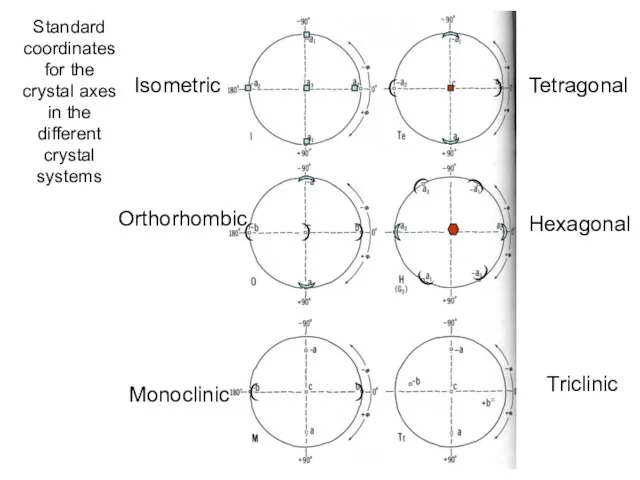
- 31. Standard coordinates for the crystal axes in the different crystal systems Isometric Tetragonal Triclinic Hexagonal Orthorhombic
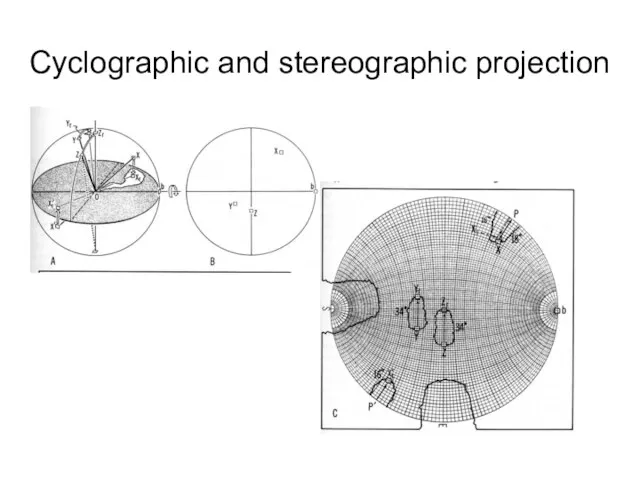
- 32. Cyclographic and stereographic projection
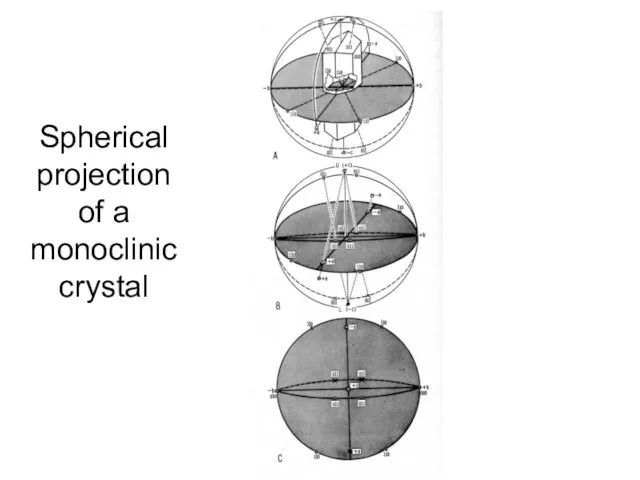
- 33. Spherical projection of a monoclinic crystal
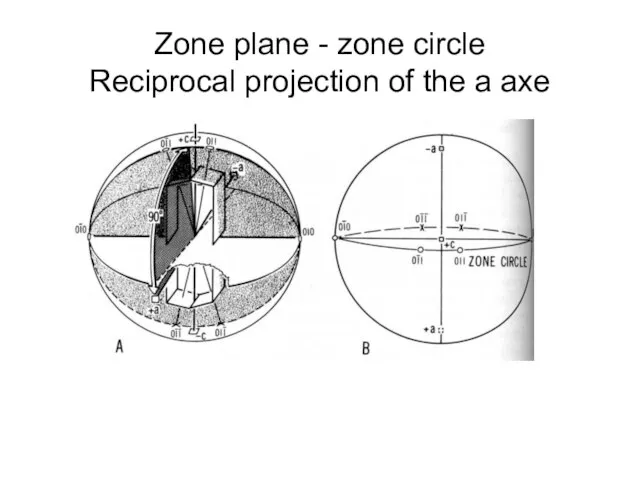
- 34. Zone plane - zone circle Reciprocal projection of the a axe
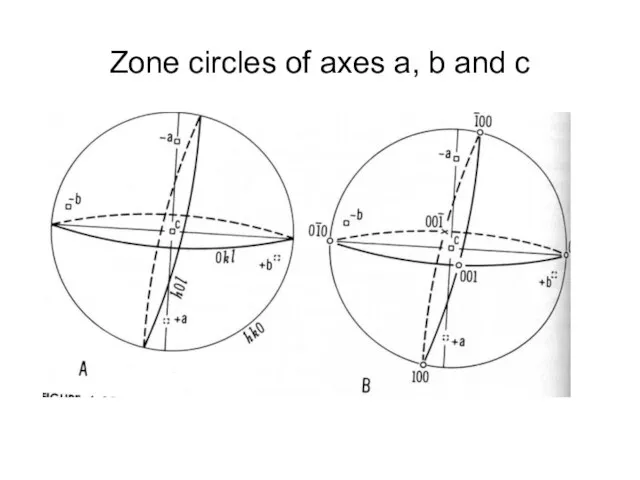
- 35. Zone circles of axes a, b and c
- 36. Cyclographic and stereographic projection
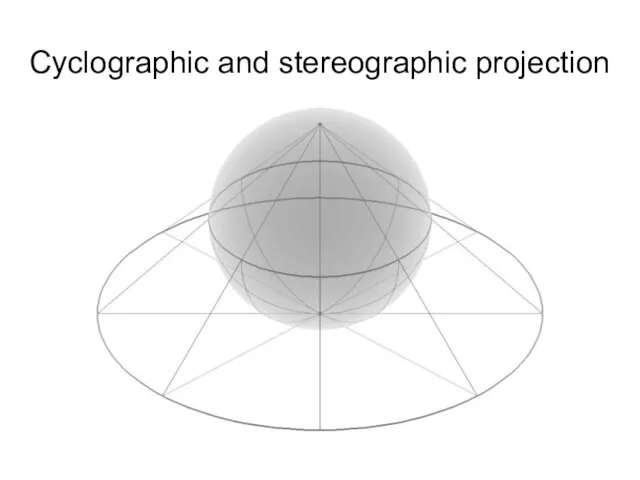
- 37. Cyclographic and stereographic projection
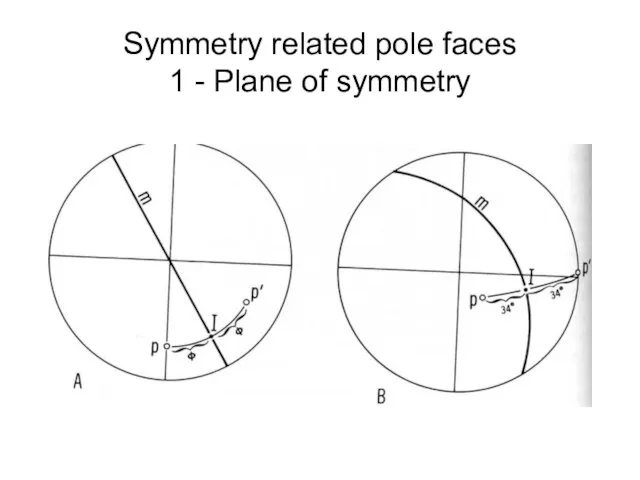
- 38. Symmetry related pole faces 1 - Plane of symmetry
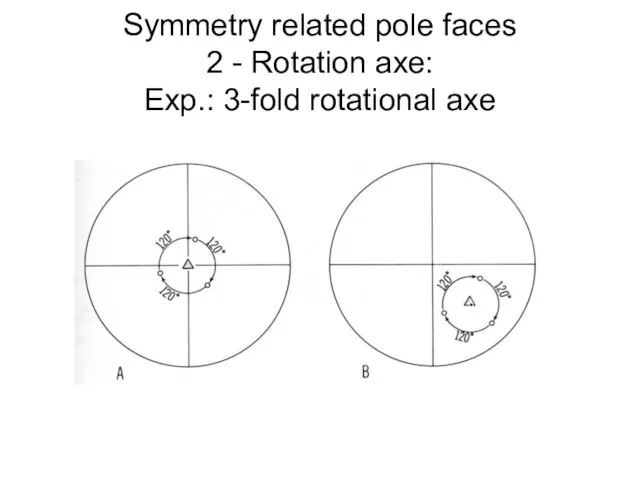
- 39. Symmetry related pole faces 2 - Rotation axe: Exp.: 3-fold rotational axe
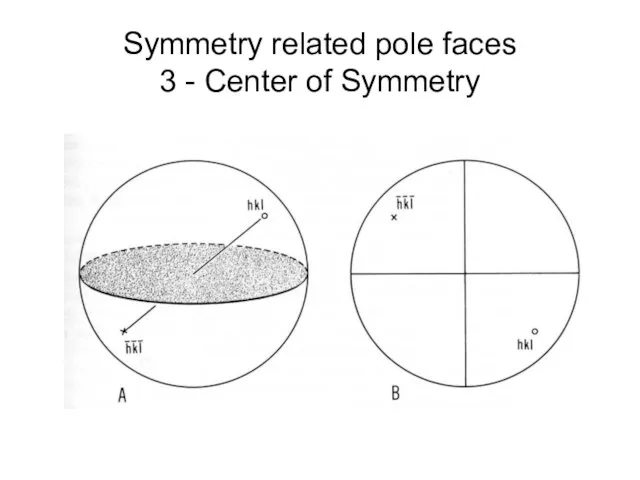
- 40. Symmetry related pole faces 3 - Center of Symmetry
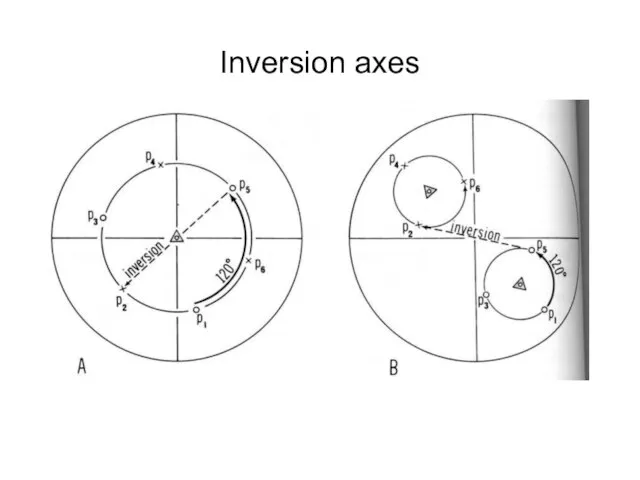
- 41. Inversion axes
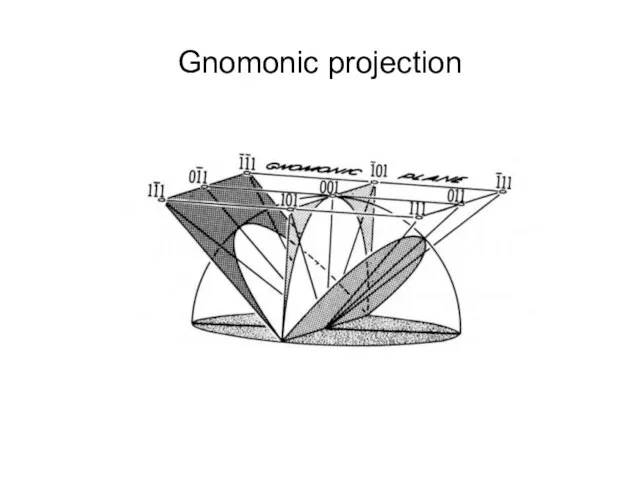
- 42. Gnomonic projection
- 44. Скачать презентацию





![Stereographic projection of crystal faces [example face (011) of a cube]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/374064/slide-19.jpg)



 photoshop
photoshop Общение родителей и детей как условие успеха воспитания
Общение родителей и детей как условие успеха воспитания Кожевенное сырье
Кожевенное сырье Волнистые попугайчики
Волнистые попугайчики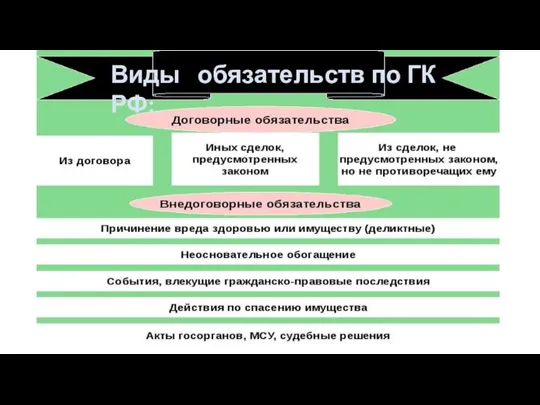 Виды обязательств в ГК РФ
Виды обязательств в ГК РФ гр право
гр право Требования к эссе. Гендерное равенство и право
Требования к эссе. Гендерное равенство и право Свет и его законы
Свет и его законы Деятельность ФСИН России
Деятельность ФСИН России Инновации в автоматизации продвижения сайтов
Инновации в автоматизации продвижения сайтов Смелый набег. Вятский край в эпоху феодализма. (9 класс)
Смелый набег. Вятский край в эпоху феодализма. (9 класс) Русское искусство первой половины XIX века
Русское искусство первой половины XIX века Valpurgiyev’s night From April 30 to May
Valpurgiyev’s night From April 30 to May Приемы развития ИСУД ученика средствами предмета
Приемы развития ИСУД ученика средствами предмета Методология научной деятельности. Тема, объект, предмет, исследования
Методология научной деятельности. Тема, объект, предмет, исследования Устройство гранаты
Устройство гранаты Виды и типы сетевых продовольственных магазинов
Виды и типы сетевых продовольственных магазинов Профессия МЕНЕДЖЕР
Профессия МЕНЕДЖЕР Международные финансовые отношения и развития валютных систем
Международные финансовые отношения и развития валютных систем Дэлхийн х?н ам
Дэлхийн х?н ам halloween_vocabulary
halloween_vocabulary Растительный и животный мир
Растительный и животный мир Схемы по Прекращению обязательств
Схемы по Прекращению обязательств Презентация на тему Пещерные храмы в Эллоре
Презентация на тему Пещерные храмы в Эллоре  Ориентирование на местности
Ориентирование на местности Методическая разработка внеаудиторного мероприятия
Методическая разработка внеаудиторного мероприятия Каталог TopFranchise. Коммерческое предложение по сотрудничеству
Каталог TopFranchise. Коммерческое предложение по сотрудничеству Шаблон для презентации
Шаблон для презентации