Содержание
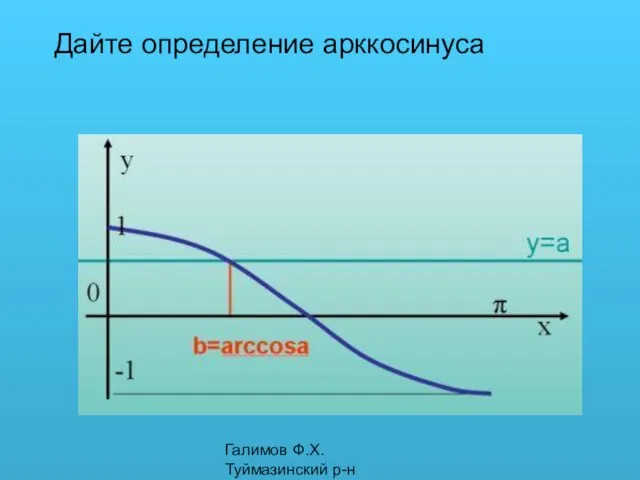
- 2. Галимов Ф.Х. Туймазинский р-н Дайте определение арккосинуса
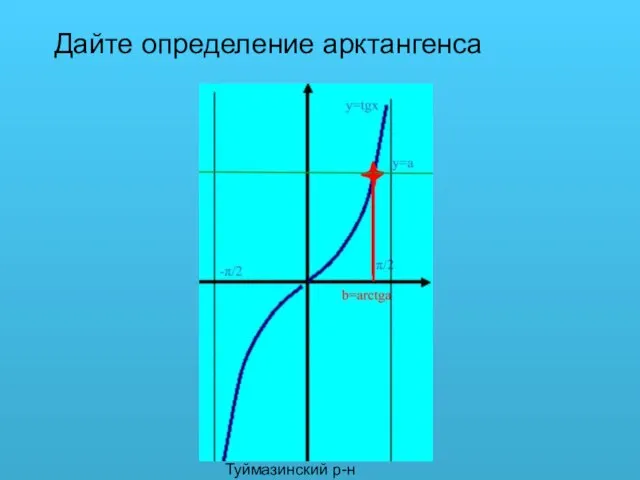
- 3. Галимов Ф.Х. Туймазинский р-н Дайте определение арктангенса
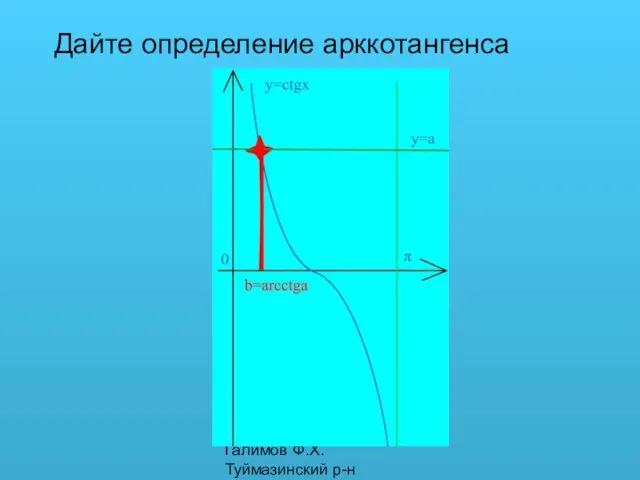
- 4. Галимов Ф.Х. Туймазинский р-н Дайте определение арккотангенса
- 5. Галимов Ф.Х. Туймазинский р-н π/4 -π/4 π/3 -π/3 0 не существует
- 6. Галимов Ф.Х. Туймазинский р-н π/4 3π/4 π/6 5π/6 не существует π/2
- 7. Галимов Ф.Х. Туймазинский р-н -π/6 π/6 5π/6 π/4 π/3 3π/4 π/4 -π/4 π/6 -π/3
- 8. Галимов Ф.Х. Туймазинский р-н Имеют ли смысл выражения? Почему?
- 9. Галимов Ф.Х. Туймазинский р-н Новая тема. Решение простейших тригонометрических уравнений
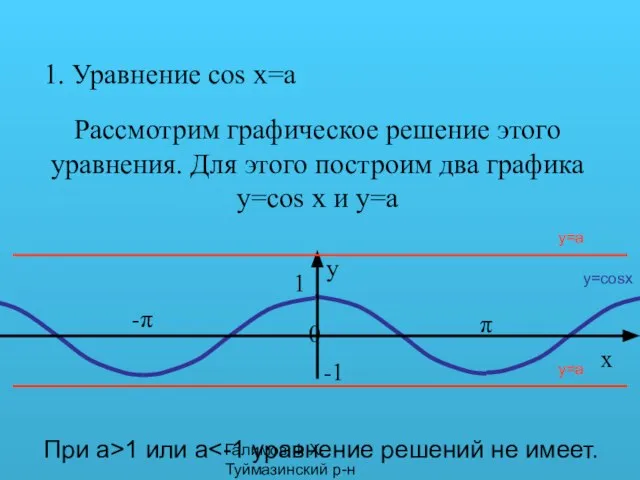
- 10. Галимов Ф.Х. Туймазинский р-н 1. Уравнение cos x=a Рассмотрим графическое решение этого уравнения. Для этого построим
- 11. Галимов Ф.Х. Туймазинский р-н y=a y=a При aЄ[-1;1] уравнение cos x=a имеет бесконечное множество решений. Мы
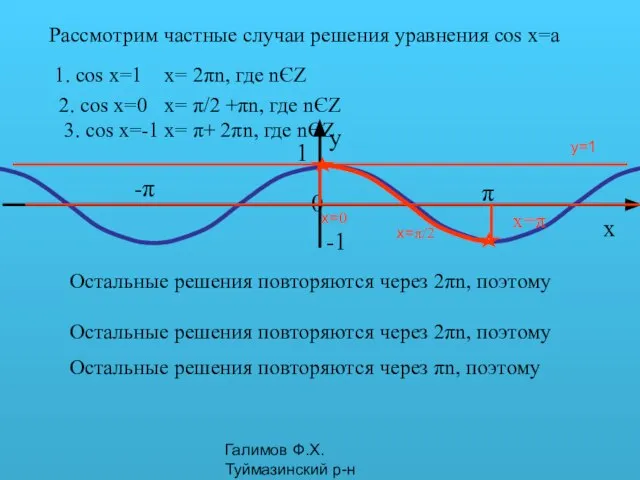
- 12. Галимов Ф.Х. Туймазинский р-н y=1 Рассмотрим частные случаи решения уравнения cos x=a 1. cos x=1 x=π/2
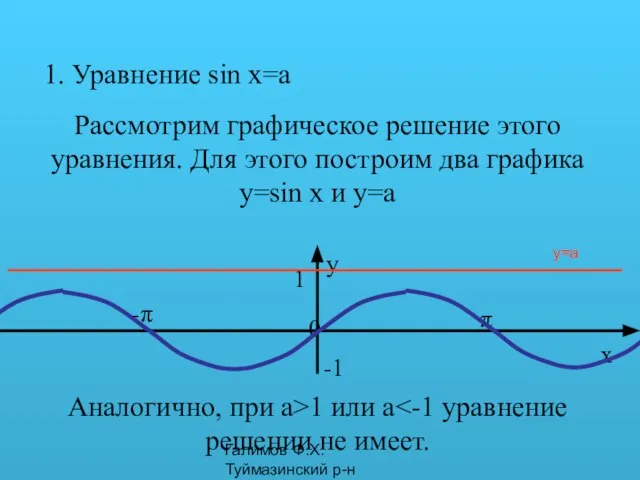
- 13. Галимов Ф.Х. Туймазинский р-н 1. Уравнение sin x=a Рассмотрим графическое решение этого уравнения. Для этого построим
- 14. Галимов Ф.Х. Туймазинский р-н y=a При aЄ[-1;1] уравнение sin x=a имеет бесконечное множество решений. Мы можем
- 15. Галимов Ф.Х. Туймазинский р-н Получаем две группы решении x1=arcsin a+ 2πn, x2= π -arcsin a+ 2πn,
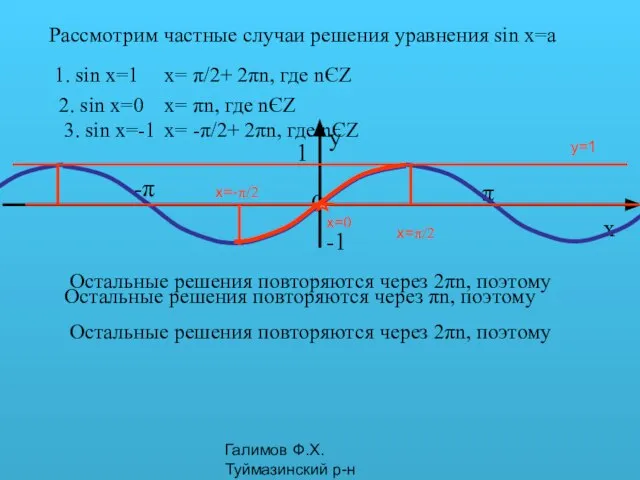
- 16. Галимов Ф.Х. Туймазинский р-н y=1 Рассмотрим частные случаи решения уравнения sin x=a 1. sin x=1 x=π/2
- 17. Галимов Ф.Х. Туймазинский р-н Решите уравнения
- 18. Галимов Ф.Х. Туймазинский р-н
- 19. Галимов Ф.Х. Туймазинский р-н
- 20. Галимов Ф.Х. Туймазинский р-н
- 21. Галимов Ф.Х. Туймазинский р-н
- 22. Галимов Ф.Х. Туймазинский р-н
- 24. Скачать презентацию
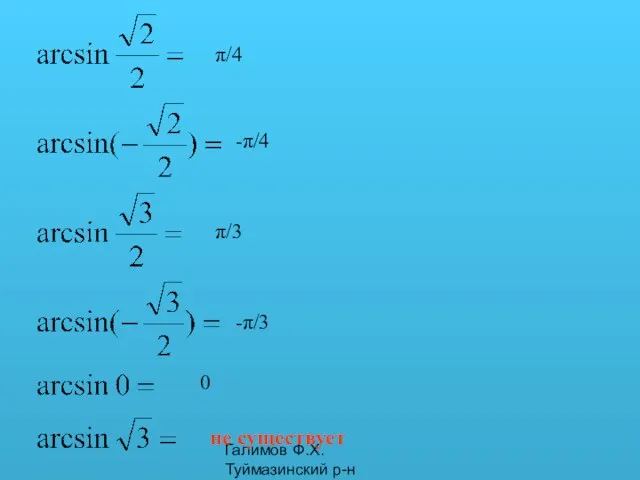




![Галимов Ф.Х. Туймазинский р-н y=a y=a При aЄ[-1;1] уравнение cos x=a имеет](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396473/slide-10.jpg)
![Галимов Ф.Х. Туймазинский р-н y=a При aЄ[-1;1] уравнение sin x=a имеет бесконечное](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/396473/slide-13.jpg)


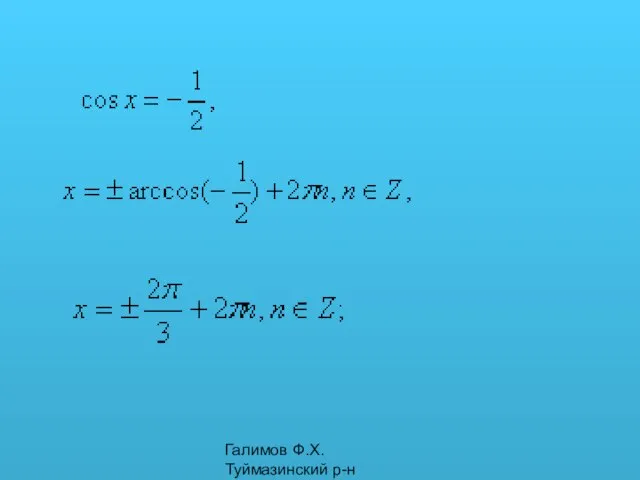
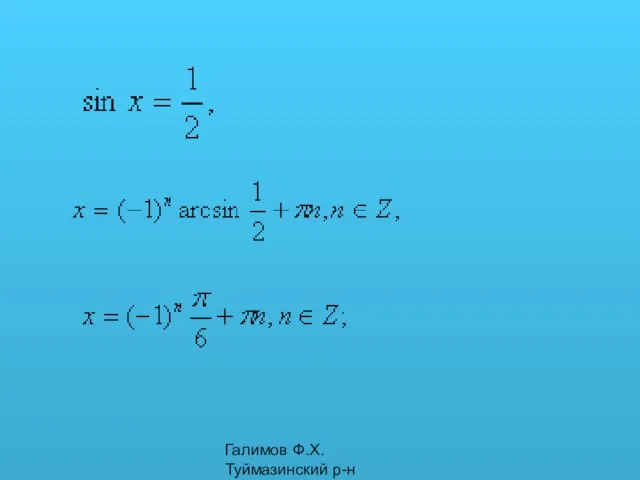



 Самые, самые в России!
Самые, самые в России! Молодежная политика
Молодежная политика Электронный портфолио педагога:
Электронный портфолио педагога: Технические характеристики силосов
Технические характеристики силосов 630979
630979 Дни воинской славы России
Дни воинской славы России МОУ «Усть – Кубинская СОШ»
МОУ «Усть – Кубинская СОШ» Мониторинг информационного сопровождения приоритетного национального проекта в сфере здравоохранения на территории Ханты-Ман
Мониторинг информационного сопровождения приоритетного национального проекта в сфере здравоохранения на территории Ханты-Ман Проектирование информационно-аналитической системы оценки эффективности факторинговых операций банка
Проектирование информационно-аналитической системы оценки эффективности факторинговых операций банка Зрительное восприятие устной речи
Зрительное восприятие устной речи Выправка стрелочного перевода двойным обжатием шпал и брусьев. Регулировка стрелочного перевода в плане
Выправка стрелочного перевода двойным обжатием шпал и брусьев. Регулировка стрелочного перевода в плане Cudzoziemiec w Polsce
Cudzoziemiec w Polsce Квест, презентация
Квест, презентация Игры на уроках истории
Игры на уроках истории Пути и формы выявления, развития и поддержки музыкально одарённых детей на примере работы ОДОД гимназии №271
Пути и формы выявления, развития и поддержки музыкально одарённых детей на примере работы ОДОД гимназии №271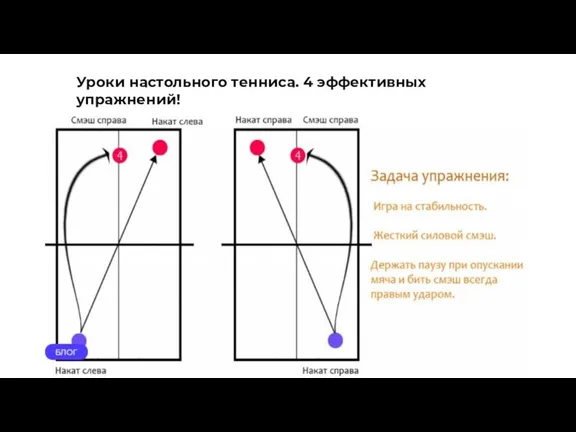 Настольный теннис. Эффективные упражнения
Настольный теннис. Эффективные упражнения Этика Севостьянов
Этика Севостьянов Основные закономерности развития науки Подготовили: студентки 1 курса РТА Группа : 1409ФТД Ломовцева Екатерина и Кройтор Татьяна
Основные закономерности развития науки Подготовили: студентки 1 курса РТА Группа : 1409ФТД Ломовцева Екатерина и Кройтор Татьяна Роль воды в жизни человека
Роль воды в жизни человека Зимняя сезонная школа
Зимняя сезонная школа Some and any
Some and any О, СПОРТ, - ТЫ МИР
О, СПОРТ, - ТЫ МИР Cловарный алгоритм. Пошаговая работа
Cловарный алгоритм. Пошаговая работа Механические волны
Механические волны Ответьте на вопросы:
Ответьте на вопросы: Инкрустация проволокой
Инкрустация проволокой Алгоритмы и исполнители
Алгоритмы и исполнители Сельское поселение Куруш муниципального образования Докузпаринский район
Сельское поселение Куруш муниципального образования Докузпаринский район