Содержание
- 2. Красный Зелёный Синий Черный Красный Подсказка: А знаете что это такое? Жёлтый Чёрный Зелёный Синий Чёрный
- 3. Красный Зелёный Синий Черный Красный Подсказка: Упражнение для развития концентрации Жёлтый Чёрный Зелёный Синий Чёрный
- 4. Красный Зелёный Синий Черный Красный Кто хочет попробовать назвать ЦВЕТА шрифта? Жёлтый Чёрный Зелёный Синий Чёрный
- 5. Возвращаемся: Что это?
- 6. Ответ Тест «на шпиона»
- 10. Тест на внимательность Сможете ли вы вспомнить, сколько различных иероглифов было на предыдущем слайде? Сколько было
- 14. Тест на удачливость Попробуйте угадать, какой иероглиф какому цвету соответствует? Жёлтый Чёрный Красный Зелёный Синий
- 15. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий
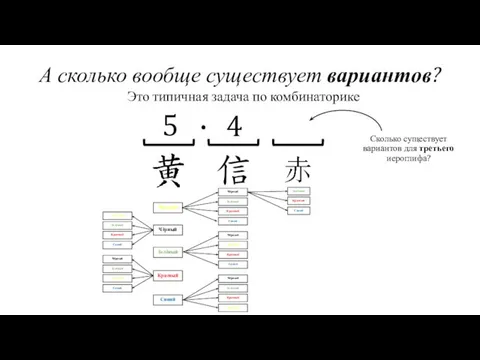
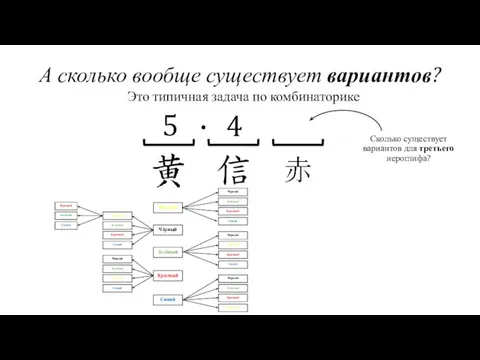
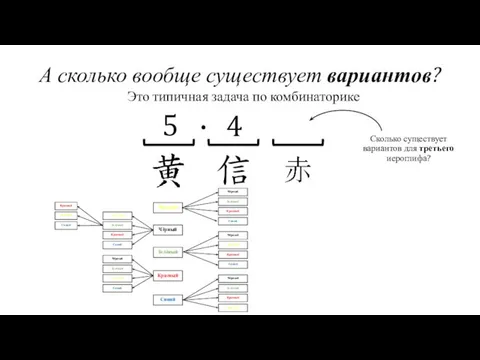
- 16. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике
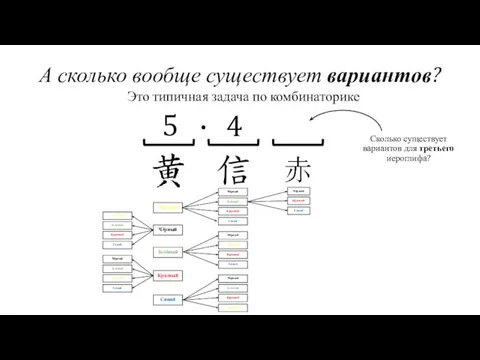
- 17. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике Сколько
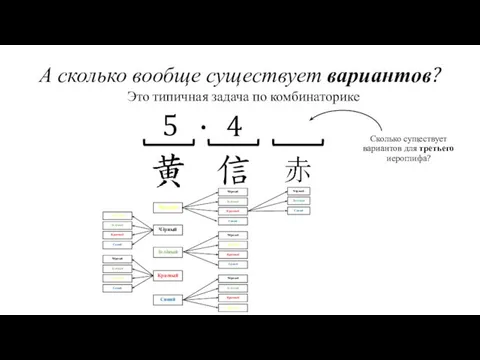
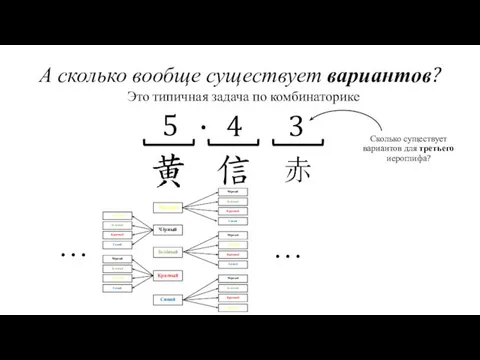
- 18. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике Сколько
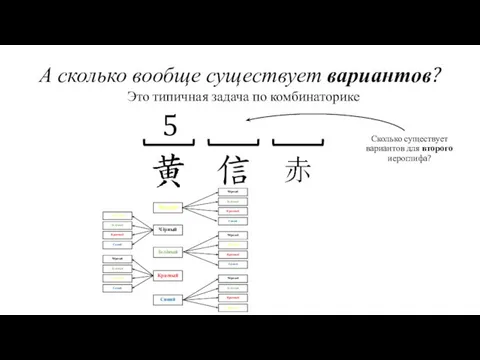
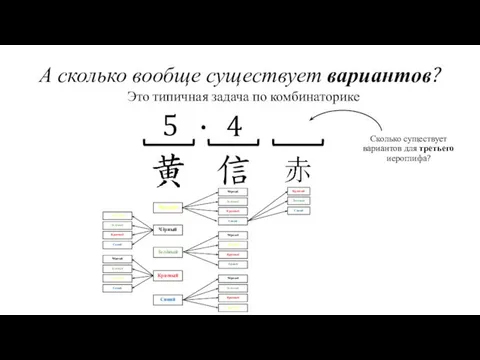
- 19. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
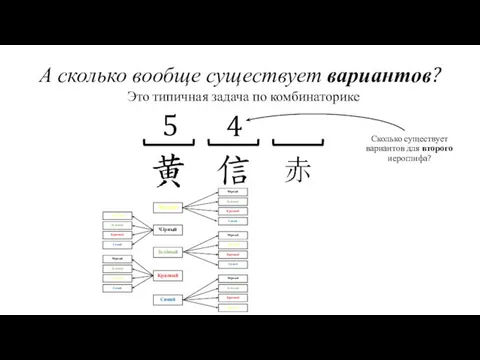
- 20. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
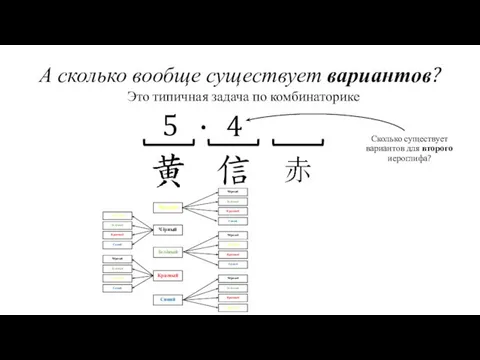
- 21. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
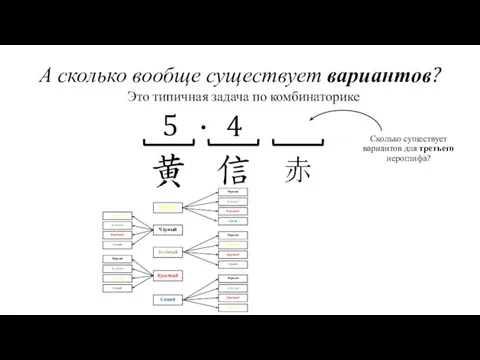
- 22. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 23. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 24. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 25. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 26. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 27. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 28. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 29. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 30. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 31. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 32. А сколько вообще существует вариантов? Жёлтый Чёрный Красный Зелёный Синий Это типичная задача по комбинаторике 5
- 33. Попробуем угадать 5 4 · 3 · = 60 Жёлтый Чёрный Красный Зелёный Синий
- 37. Попробуем угадать 5 4 · 3 · = 60 Жёлтый Красный Синий
- 38. Река = ?
- 39. Река = Хуанхэ
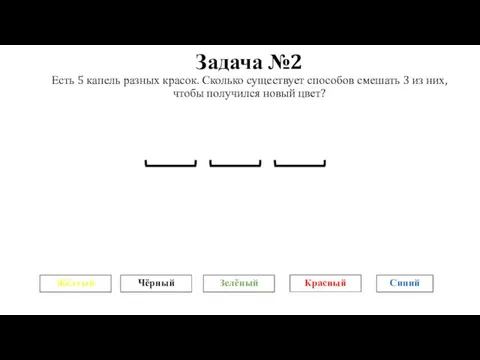
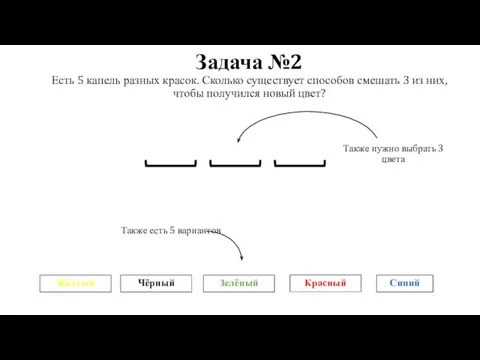
- 40. Задача №2 Есть 5 капель разных красок. Сколько существует способов смешать 3 из них, чтобы получился
- 41. Задача №2 Есть 5 капель разных красок. Сколько существует способов смешать 3 из них, чтобы получился
- 42. Задача №2 Есть 5 капель разных красок. Сколько существует способов смешать 3 из них, чтобы получился
- 43. Задача №2 Есть 5 капель разных красок. Сколько существует способов смешать 3 из них, чтобы получился
- 44. Задача №2 Вот все 60 вариантов из первой задачи: ЧЖК ЧЖС ЧЖЗ ЧКЖ ЧКС ЧКЗ ЧСЖ
- 45. Задача №2 Самостоятельно выпишите номера вариантов, совпадающих с первым. ЧЖК ЧЖС ЧЖЗ ЧКЖ ЧКС ЧКЗ ЧСЖ
- 46. Задача №2 Самостоятельно выпишите номера вариантов, совпадающих с первым. ЧЖК ЧЖС ЧЖЗ ЧКЖ ЧКС ЧКЗ ЧСЖ
- 47. Задача №2 Самостоятельно выпишите номера вариантов, совпадающих с 29-ым. ЧЖК ЧЖС ЧЖЗ ЧКЖ ЧКС ЧКЗ ЧСЖ
- 48. Задача №2 Самостоятельно выпишите номера вариантов, совпадающих с 29-ым. ЧЖК ЧЖС ЧЖЗ ЧКЖ ЧКС ЧКЗ ЧСЖ
- 49. Получается, в прежних вычислениях каждый вариант учтен 6 раз 5 4 · 3 · = 60
- 50. Значит, для решения второй задачи, ответ первой задачи надо поделить на 6. 5 4 · 3
- 51. Очень часто в задачах по комбинаторике Надо понять: делить или не делить?
- 52. Распространенный алгоритм Количество позиций. Сколько элементов надо выбрать? (3) Количество элементов. Сколько ВСЕГО есть вариантов заполнения
- 53. Решаем задачи
- 55. Скачать презентацию






































 Владимир Владимир Маяковский
Владимир Владимир Маяковский  Кукольный спектакль Зайкина тётя
Кукольный спектакль Зайкина тётя Презентация на тему Язык HTML
Презентация на тему Язык HTML Культура во второй половине XX-начале XXI века.
Культура во второй половине XX-начале XXI века. Сделай свое лето со 2 июня по 3 августа 2019 года включительно (период действия каталогов №№8–10 2019 года)
Сделай свое лето со 2 июня по 3 августа 2019 года включительно (период действия каталогов №№8–10 2019 года) Презентация на тему: Информация, как основная сущность теории информации
Презентация на тему: Информация, как основная сущность теории информации Тип губки
Тип губки использование религиозных символов в коммерческой рекламе
использование религиозных символов в коммерческой рекламе Prezentatsia1
Prezentatsia1 A real professional. What does it mean?
A real professional. What does it mean? Santa Claus
Santa Claus Внутренняя политика России в начале XXI века – восстановление государства
Внутренняя политика России в начале XXI века – восстановление государства Общественная жизнь России при Николае I
Общественная жизнь России при Николае I Le frasi ridicole
Le frasi ridicole Предложения по подготовке специалистовдля реализации проектов по коммерциализации товаров и услуг ГНСС «ГЛОНАСС»
Предложения по подготовке специалистовдля реализации проектов по коммерциализации товаров и услуг ГНСС «ГЛОНАСС» Создание культурной среды при обучении младших школьников иностранному языку
Создание культурной среды при обучении младших школьников иностранному языку Технические кодексы установившейся практики в области охраны окружающей среды и природопользования
Технические кодексы установившейся практики в области охраны окружающей среды и природопользования Одуванчик
Одуванчик Введение в теорию производства
Введение в теорию производства "ПО ДОРОГАМ ГРАЖДАНСКОЙ ВОЙНЫ"
"ПО ДОРОГАМ ГРАЖДАНСКОЙ ВОЙНЫ" Как фотографировать высокое сооружение
Как фотографировать высокое сооружение Презентация на тему Роль права в жизни государства
Презентация на тему Роль права в жизни государства Презентация на тему Деревья леса
Презентация на тему Деревья леса l_sapr_1-7
l_sapr_1-7 Эффективные способы использования заемных средств, способствующие развитию бизнеса.
Эффективные способы использования заемных средств, способствующие развитию бизнеса. Алиса в стране чудес
Алиса в стране чудес Добровольцы мы (3 раза) В армии Христа. Смело мы идем за своим Вождем, С Ним мы победим врага.
Добровольцы мы (3 раза) В армии Христа. Смело мы идем за своим Вождем, С Ним мы победим врага. Особенности проведенияЕГЭв штатном режиме
Особенности проведенияЕГЭв штатном режиме