Дефекты упорядочивающихся сплавов

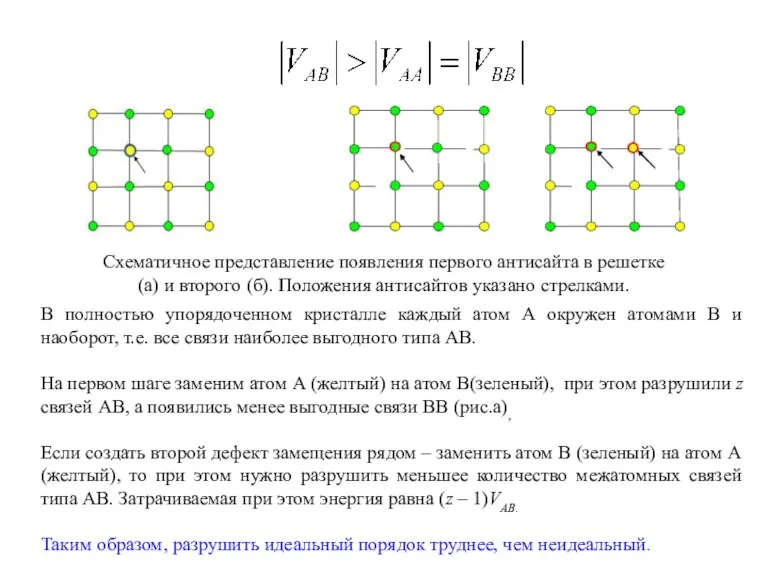
Схематичное представление появления первого антисайта в решетке (а) и второго (б). Положения антисайтов указано стрелками.
В полностью упорядоченном кристалле каждый атом А окружен атомами В и наоборот, т.е. все связи наиболее выгодного типа АВ.
На первом шаге заменим атом А (желтый) на атом В(зеленый), при этом разрушили z связей АВ, а появились менее выгодные связи ВВ (рис.а),
Если создать второй дефект замещения рядом – заменить атом В (зеленый) на атом А (желтый), то при этом нужно разрушить меньшее количество межатомных связей типа АВ. Затрачиваемая при этом энергия равна (z – 1)VAB.
Таким образом, разрушить идеальный порядок труднее, чем неидеальный.

Метрика дальнего порядка в упорядочивающихся сплавах
Рассмотрим сплав AnBm, в котором есть две подрешетки: α, β.
Пусть NA, NB – полное количество атомов сорта A и B,
NA+NB=N – полное число атомов в сплаве.
Далее пусть Lα, Lβ – число узлов подрешеток первого и второго типа.
Стехиометрический состав NA=Lα , NB=Lβ
– общее число узлов кристалла.
Введем величины
– количество атомов сортов A и B на подрешетках.
предположение

Метрика дальнего порядка в упорядочивающихся сплавах
Уход атома сорта A на чужую подрешетку β должен сопровождаться переходом атома сорта B на подрешетку α.
Других альтернатив нет, поскольку только замещения, а вакансий нет .
Из этого следует, абсолютное число дефектов замещения на подрешетках должно быть равным.
.
полное упорядочение
хаотическое заполнение –полный беспорядок

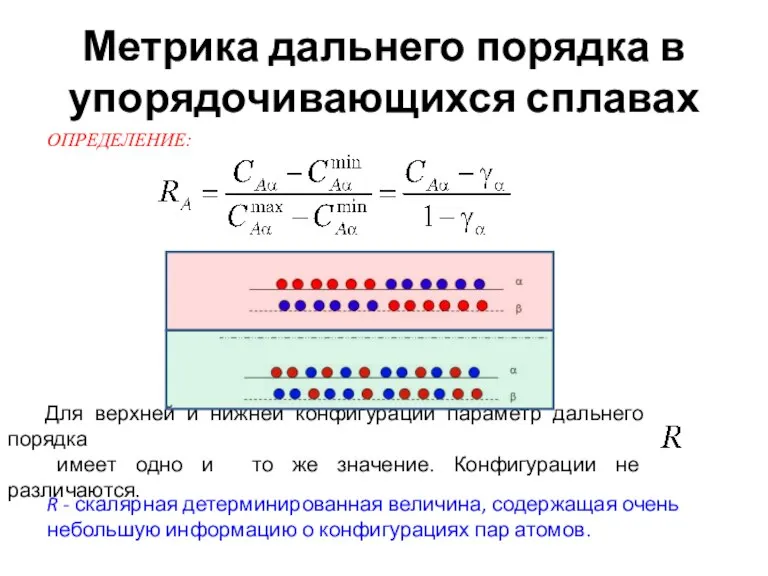
Метрика дальнего порядка в упорядочивающихся сплавах
Для верхней и нижней конфигураций параметр дальнего порядка
имеет одно и то же значение. Конфигурации не различаются.
.
R - скалярная детерминированная величина, содержащая очень небольшую информацию о конфигурациях пар атомов.
ОПРЕДЕЛЕНИЕ:

Метрика ближнего порядка в упорядочивающихся сплавах. Связь дальнего порядка и среднего значения ближнего порядка в упорядочивающихся сплавах

Метрика ближнего порядка в упорядочивающихся сплавах
Более детальный подход – подсчет числа конфигураций, возможных в данной структуре и при данной заселенности подрешеток, т.е. заданном значении дальнего параметра порядка. Рассмотрим упрощенный подход, не рассматривая геометрию конфигурации, а рассматривая только число пар атомов разного сорта.
QAB – числом правильных пар атомов, то есть пар, в которых атом А находится на подрешетке α, а атом B на подрешетке β.
QBA – числом неправильных пар: атом А – на подрешетке β, атом B – на подрешетке α.
Доля смешанных пар типа AB (BA) есть:
q=(QAB + QBA)/ Q,
где Q – полное число пар: Q = QAB + QBA + QBB + QAA =Nz1/2 .
Число ближайших соседей z1 в первой координационной сфере будем предполагать одинаковым для подрешеток структуры.

Введем параметр ближнего порядка как:
,
где qmin – минимальное количество пар типа AB (BA), qmax – максимальное количество пар.
В случае полного порядка, имеем: q=qmax, σ=1.
Все конфигурации одинаковые - флуктуаций нет.
При полном беспорядке: q=qmin, σ=0, но флуктуации должны быть большими, поскольку при беспорядке встречаются различные конфигурации окружения. σ – случайная величина.
Как отмечалось, заданному набору чисел NAα, NBβ, NBα, NAβ соответствует одно значение дальнего порядка. Однако, этому набору чисел заполнения соответствует множество различных конфигураций пар QAB , QBA , QBB , QAA.
Параметр порядка R может быть функцией только среднего значения параметра σ. Усреднение должно проводиться по функции распределения вероятности обнаружения различных конфигураций, которая определяется как структурой подрешеток, их заселенностью атомами, так и взаимодействием последних,
т.е. R=f(< σ >) связь весьма сложная.

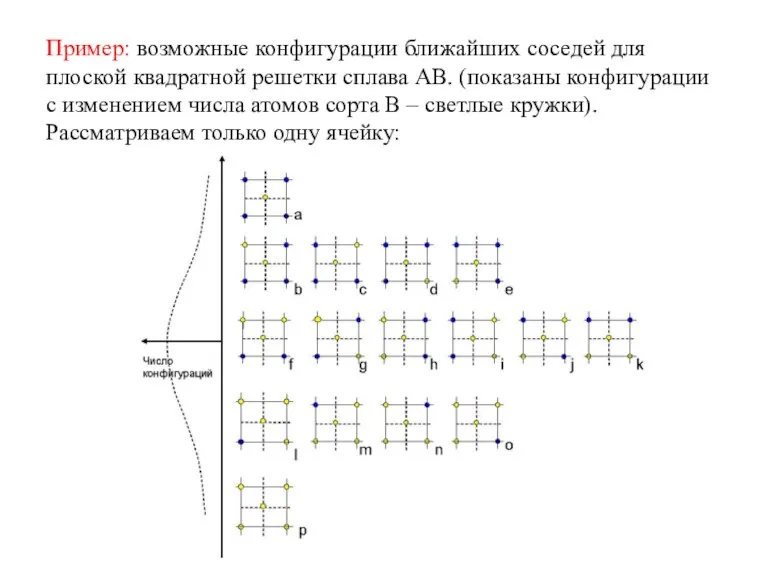
Пример: возможные конфигурации ближайших соседей для плоской квадратной решетки сплава АВ. (показаны конфигурации с изменением числа атомов сорта В – светлые кружки). Рассматриваем только одну ячейку:

Представим среднюю вероятность найти правильную пару (АВ) в приближении независимости концентраций атомов на различных подрешетках:
Концентрации собственных атомов можно выразить через параметр дальнего порядка (заметим, что γB=1 - γA):
CAα= γBR+ γA; CBβ= γAR+ γB
Концентрации дефектов замещения определяются через R и условия сохранения числа атомов данного сорта и числа узлов подрешеток в условиях стехиометрии и отсутствия вакансий:
Аналогично, CBα= γB(1-R) . Отсюда средняя доля смешанных пар:

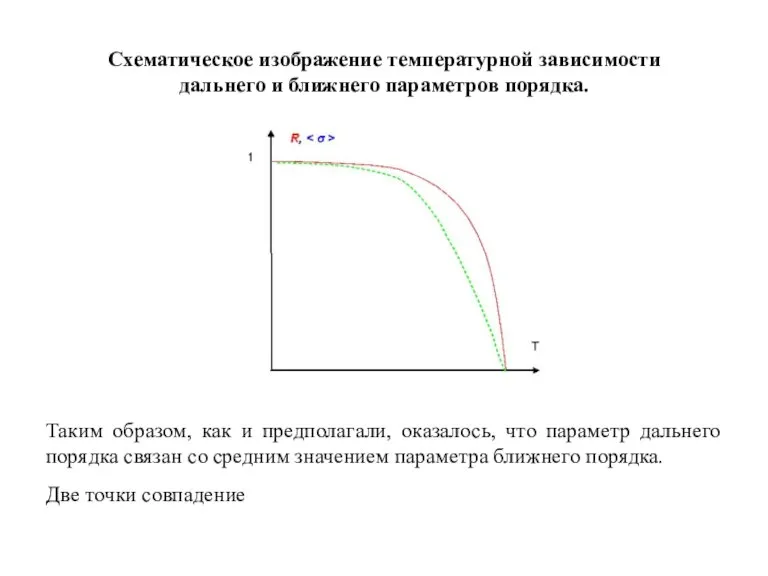
Схематическое изображение температурной зависимости
дальнего и ближнего параметров порядка.
Таким образом, как и предполагали, оказалось, что параметр дальнего порядка связан со средним значением параметра ближнего порядка.
Две точки совпадение

Температурная зависимость концентрации равновесных дефектов замещения в упорядочивающихся сплавах
Допустим, известен способ, которым можно получить статистическую сумму по ансамблю различных состояний кристалла, имеющих одинаковые значения параметра дальнего порядка R, но отличающихся значением параметра ближнего порядка.
Статистическая сумма равна , где:
ν – индекс различных мод колебаний для данной конфигурации,
k – индекс состояний, отвечающий различным конфигурациям кристалла для данного значения дальнего порядка,
Wk – конфигурационная энергия кристалла (потенциальная энергия данной конфигурации),
– колебательная энергия кристалла для моды ν и конфигурации k.

Зная статистическую сумму Z(R) , можно получить величину свободной энергии F(R) ≡ - kT⋅lnZ(R).
Равновесие системы достигается при минимуме свободной энергии F(R) по изменяемой величине.
Отсюда из условия
можно найти равновесные значения дальнего порядка R* и получить равновесную концентрацию антисайтов .
Используем приближения:
Колебательная часть теплоемкости слабо зависит от конфигурации кристалла → заменяем ее на константу для упрощения расчета статсуммы.
Учитываем только парные взаимодействия при расчете конфигурационной энергии кристалла
Используем приближение Брэгга-Вилсона для суммирования статсуммы

Итак, выражение для статистической суммы можно переписать в виде
Для вычисления последнего выражения необходимо знание Zkν, для вычисления которой необходим анализ спектра колебаний данной конфигурации структуры, поскольку в общем случае спектр меняется при изменении конфигурации. Если предположить, что Zkν слабо зависит от конфигурации k, то формально можно вынести Zkν за знак суммы по k
Это утверждение находит экспериментальное подтверждение, например, для β-латуни в интервале температур Т≈550÷750К упорядочение резко меняется, но колебательная часть теплоемкости меняется слабо, т.е. Zkν≈ Zν, в отличии от конфигурационной составляющей . Для конфигурационной части статистической суммы можно записать
Рассмотрим систему в приближении парного взаимодействия. Причем предположим, что взаимодействие между атомами: -VAA, -VBB, -VAB.
Количество различных взаимодействующих пар атомов: QAA, QBB, QAB, QBA

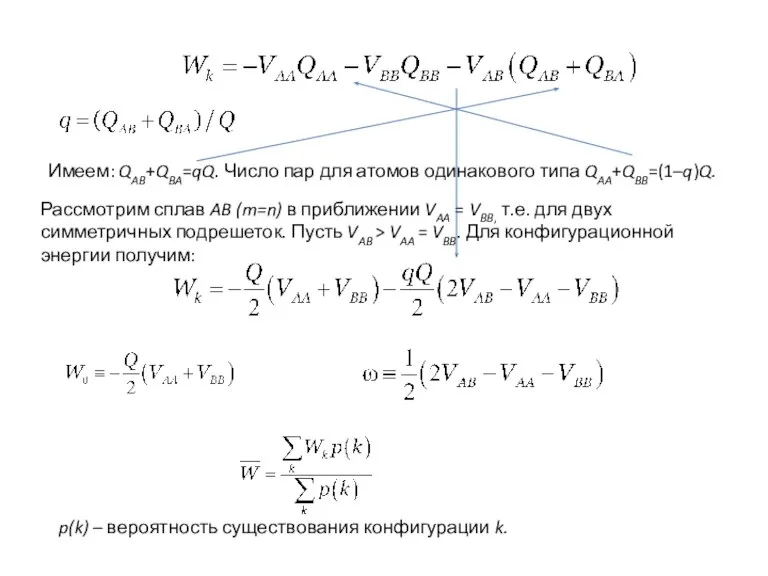
Рассмотрим сплав AB (m=n) в приближении VAA = VBB, т.е. для двух симметричных подрешеток. Пусть VAB > VAA = VBB. Для конфигурационной энергии получим:
Имеем: QAB+QBA=qQ. Число пар для атомов одинакового типа QAA+QBB=(1–q)Q.
p(k) – вероятность существования конфигурации k.

энергия кристалла при полном беспорядке.
Пусть вероятность найти возможные при данном значении R конфигурации одна и та же. Тогда средняя конфигурационная энергия равна

– число возможных конфигураций для данного значения дальнего порядка.
В качестве нужно взять число способов размещения NAα атомов сорта А по подрешетке α, NBα атомов сорта B по подрешетке α, NAβ атомов сорта А по подрешетке β и NBβ атомов сорта B по подрешетке β:

разложим в ряд относительно среднего значения
:
Ограничиваясь приближением среднего поля (или приближением Брэгга-Вильямсона, что для кристаллов то же самое), то есть, оставляя единственное слагаемое с j = 0 (M0 = 1) в разложении, получаем

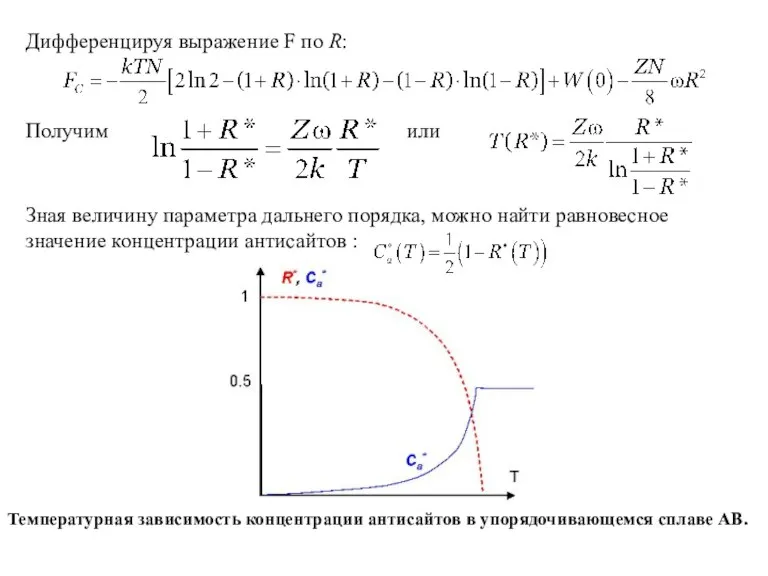
Дифференцируя выражение F по R:
Получим или
Зная величину параметра дальнего порядка, можно найти равновесное значение концентрации антисайтов :
Температурная зависимость концентрации антисайтов в упорядочивающемся сплаве АВ.

Температурная зависимость концентрации равновесных вакансий в упорядочивающихся сплавах
Антисайт в сплаве может образоваться различными способами. Например, возможно, что атомы, расположенные на соседних подрешетках, обменяются местами. Такой процесс требует координированного движения двух атомов, поэтому вероятность его невелика.
Однако, при наличии вакансии, атом может прыгнуть на чужую подрешетку, просто заняв ее место. Следовательно, вакансия – катализатор кинетических процессов. Вопрос концентрации вакансий в упорядочивающихся сплавах важен именно для кинетики процессов упорядочения.
Рассмотрим кристалл с вакансиями. Введем следующую упрощающую модель: пусть вновь антисайты рождаются только за счет двойного обмена атомами. Поскольку состояние равновесия не зависит от того, каким способом в него пришли, то рассмотрим переход в равновесное состояние, разделенный на два этапа:
Стартуем с полностью упорядоченной конфигурации. Введем в кристалл равновесное число вакансий, не меняя распределения атомов по подрешеткам. При этом количество вакансий на подрешетках α и β будет равно NVα, NVβ соответственно.
За счет обмена атомов местами добавим в систему антисайты при этом, в соответствии с нашей моделью, мы получим равновесное состояние кристалла.

Отметим, что в силу того, что количества “своих” и “чужих” атомов на обеих подрешетках совпадают – NAα=NBβ и NAβ=NBα. И поскольку мы имеем дело со сплавом AB, то есть Lα=Lβ, то из соотношений
получаем NVα=NVβ.
Параметр дальнего порядка можно ввести и при наличии вакансий:
Аналогично можно записать и выражение для RB. Отметим, что, воспользовавшись предложенной моделью, можно показать, что упорядоченность рассматриваемой системы может характеризоваться единым параметром порядка .

Температурная концентрации антисайтов и эффективной энергии образования вакансий.
Используя тот же алгоритм расчета, что и в первом случае равновесных вакансий можно получить:
Где
VAA - взаимодействие между атомами сорта A
VAB - взаимодействие между атомами сорта A и B
Чтобы соединение было бы упорядочивающимся, необходимо выполнение соотношения: VAB > VAA, VBB.
Из полученного результата в предельном случае(VAB =VAA=VBB) можно получить арениусовскую зависимость концентрации вакансий от температуры для монокомпонентного вещества:

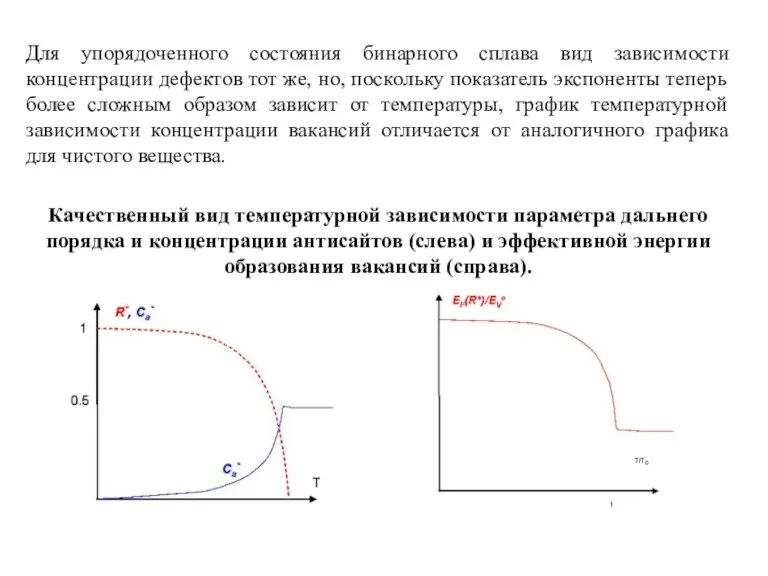
Для упорядоченного состояния бинарного сплава вид зависимости концентрации дефектов тот же, но, поскольку показатель экспоненты теперь более сложным образом зависит от температуры, график температурной зависимости концентрации вакансий отличается от аналогичного графика для чистого вещества.
Качественный вид температурной зависимости параметра дальнего порядка и концентрации антисайтов (слева) и эффективной энергии образования вакансий (справа).