Содержание
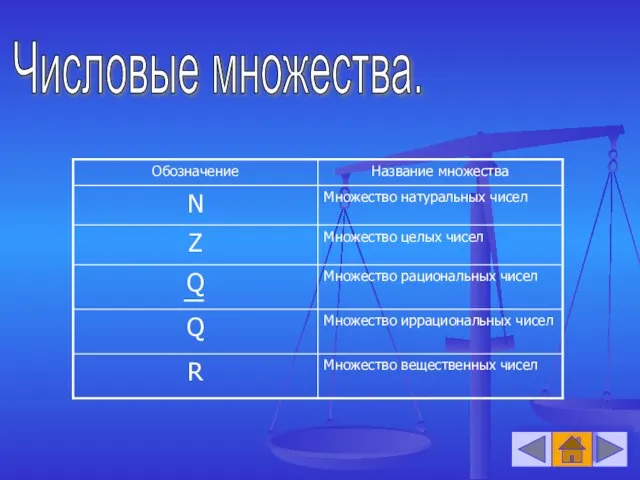
- 2. Числовые множества.
- 3. Множество натуральных чисел. Натуральные числа - это числа счета. N={1,2,…n,…}. Заметим, что множество натуральных чисел замкнуто
- 4. Множество целых чисел. Введем в рассмотрение новые числа: 1) число 0 (ноль), 2) число (-n), противоположное
- 5. Деление с остатком. В общем случае действие деления в множестве целых чисел не выполняется, но известно,
- 6. ПРИМЕРЫ: Разделить с остатком m на n. 1). m=190, n=3 190 3 18 6 3 10
- 7. Множество рациональных чисел. Множество рациональных чисел можно представить в виде: В частности, Таким образом, Множество рациональных
- 8. Но в множестве рациональных чисел нельзя, например, измерить гипотенузу прямоугольного треугольника с катетам . По теореме
- 9. Множество иррациональных чисел. Числа, которые представляются бесконечной непериодической дробью, будем называть иррациональными. Множество иррациональных чисел обозначим
- 10. Число «пи» Отношение длины окружности к диаметру есть величина постоянная, равная числу d
- 11. Число е. Если рассмотреть числовую последовательность: с общим членом последовательности то с ростом п значения будут
- 12. Известно, что мощность иррациональных чисел больше мощности рациональных, т.е. Иррациональных чисел «больше», чем рациональных. Кроме того,
- 13. Множество вещественных (действительных) чисел. Множество вещественных чисел – это объединение множества рациональных чисел. Вывод: (см. рис.
- 14. Определение модуля вещественного числа 1) Пусть на числовой оси точка А имеет координату а. Расстояние от
- 15. Например: Замечание. Определение модуля можно расширить: Пример. Раскрыть знак модуля.
- 16. Основные свойства модуля 1) 2) 3) 4) 5) 6)
- 18. Скачать презентацию














 Презентация на тему Предложения с вводными конструкциями (8 класс)
Презентация на тему Предложения с вводными конструкциями (8 класс) Салон красоты De’Paris. Издержки
Салон красоты De’Paris. Издержки ВЛАСТЬ и НАРОД в сатире М.Е.Салтыкова-Щедрина «История одного города»
ВЛАСТЬ и НАРОД в сатире М.Е.Салтыкова-Щедрина «История одного города» The system of State bodies of India
The system of State bodies of India Генерация идей и оценка их привлекательности
Генерация идей и оценка их привлекательности ГИПЕРЛИПИДЕМИЯ
ГИПЕРЛИПИДЕМИЯ  Семья и школа
Семья и школа Электронное портфолиоили Персональный сайт учителя
Электронное портфолиоили Персональный сайт учителя ВиртуализацияMicrosoft Application Virtualization 4.6(ранее SoftGrid)Демонстрация.
ВиртуализацияMicrosoft Application Virtualization 4.6(ранее SoftGrid)Демонстрация. Технологическое оборудование
Технологическое оборудование Шаблон проекта
Шаблон проекта Переформулировки поисковых запросов в Яндексе
Переформулировки поисковых запросов в Яндексе Чершкало Светлана Сергеевна
Чершкало Светлана Сергеевна Презентация на тему Малайзия (малайск. Malaysia)
Презентация на тему Малайзия (малайск. Malaysia) 点击添加相关文字内容
点击添加相关文字内容 Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  Задачи по теме
Задачи по теме Новогодние игрушки и поделки (2 часть)
Новогодние игрушки и поделки (2 часть) Методические особенности развития прыгучести у волейболистов
Методические особенности развития прыгучести у волейболистов .
. Пирĕн тăрăхри йывăçсем
Пирĕн тăрăхри йывăçсем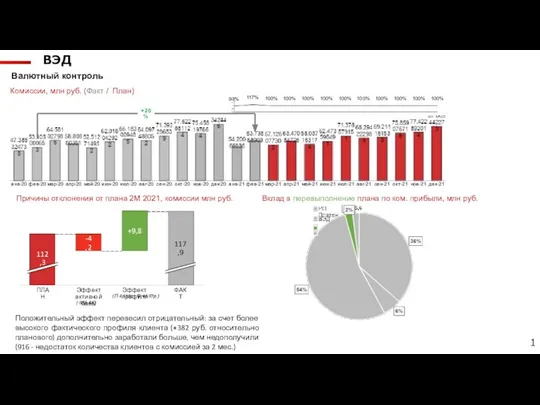 Валютный контроль
Валютный контроль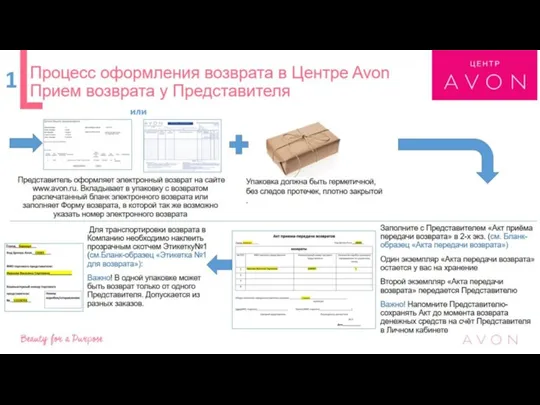 Прием возвратов у представителя в центре Avon
Прием возвратов у представителя в центре Avon Параолимпийцы Оренбургской области
Параолимпийцы Оренбургской области Презентация на тему Оптика Атомная и ядерная физика
Презентация на тему Оптика Атомная и ядерная физика Вироби зі скла. Сходи
Вироби зі скла. Сходи Алан Милн
Алан Милн Я - иллюстратор детских книг
Я - иллюстратор детских книг