Дифракция света

Дифракция света
- приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. При этом образуется интерференционная картина. Т.е. дифракция света сопровождается интерференцией.
Интерферируют волны, обогнувшие препятствие .

Дифракционная картина – система чередующихся светлых и темных колец, если препятствие круг или отверстие.
Если препятствие имеет линейный характер (щель, нить, край экрана), то на экране возникает система параллельных дифракционных полос.

Между интерференцией и дифракцией нет существенного физического различия. По историческим причинам перераспределение интенсивности, возникающее в результате суперпозиции волн от конечного числа дискретных источников, называется интерференцией. Суперпозиция волн от источников, расположенных непрерывно – дифракция.
поскольку перераспределение энергии является интерференционным, волны должны быть когерентными и для наблюдения дифракции.
дифракция
дифракции Фраунгофера
дифракции Френеля
если источник света и точка наблюдения расположены от препятствия настолько далеко, что лучи, падающие на препятствия и лучи, идущие в точку наблюдения, образуют практически параллельные пучки, говорят о дифракции в параллельных лучах
В случае расходящихся или сходящихся пучков света

Принцип Гюйгенса
каждая точка, до которой доходит волна, служит
центром вторичных волн, а огибающая этих волн
даёт положение волнового фронта в последующий
момент времени

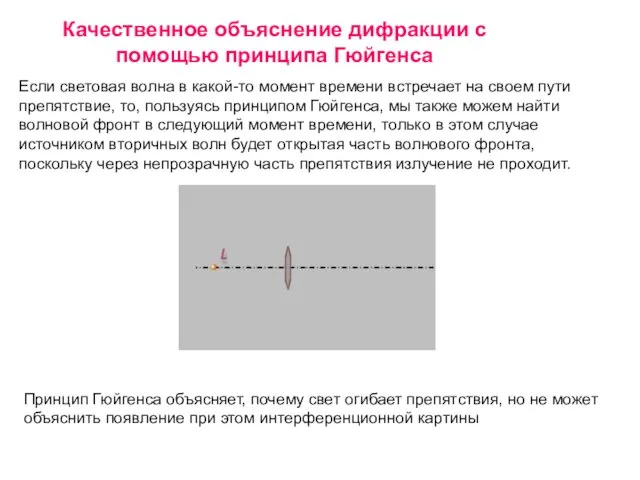
Если световая волна в какой-то момент времени встречает на своем пути препятствие, то, пользуясь принципом Гюйгенса, мы также можем найти волновой фронт в следующий момент времени, только в этом случае источником вторичных волн будет открытая часть волнового фронта, поскольку через непрозрачную часть препятствия излучение не проходит.
Качественное объяснение дифракции с помощью принципа Гюйгенса
Принцип Гюйгенса объясняет, почему свет огибает препятствия, но не может объяснить появление при этом интерференционной картины

Для объяснения появления интерференционной картины Френель дополнил принцип Гюйгенса методом расчета амплитуды результирующей волны в точке наблюдения. Согласно Френелю, световое поле в некоторой точке пространства является результатом интерференции вторичных источников.
Результирующее колебание в точке Р представляет собой суперпозицию колебаний вторичных элеменарных источников, взятых для всей поверхности S волнового фронта:
Принцип Гюйгенса-Френеля
Френель предложил оригинальный и чрезвычайно наглядный метод группировки вторичных источников. Этот метод позволяет приближенным способом очень просто, без сложных вычислений, рассчитывать дифракционные картины, и носит название метода зон Френеля.
где (ωt + α0) − фаза колебания в месте расположения волновой поверхности S, k − волновое число, r − расстояние от элемента поверхности dS до точки P, в которую приходит колебание. Множитель а0 определяется амплитудой светового колебания в месте наложения элемента dS. Коэффициент K зависит от угла φ между нормалью к площадке dS и направлением на точку Р. При φ = 0 этот коэффициент максимален, а при φ/2 он равен нулю.

Зоны Френеля
Для того чтобы найти амплитуду световой волны от точечного монохроматического источника света S в произвольной точке P изотропной среды, надо источник света окружить сферой радиусом r=ct
(это-волновой фронт)

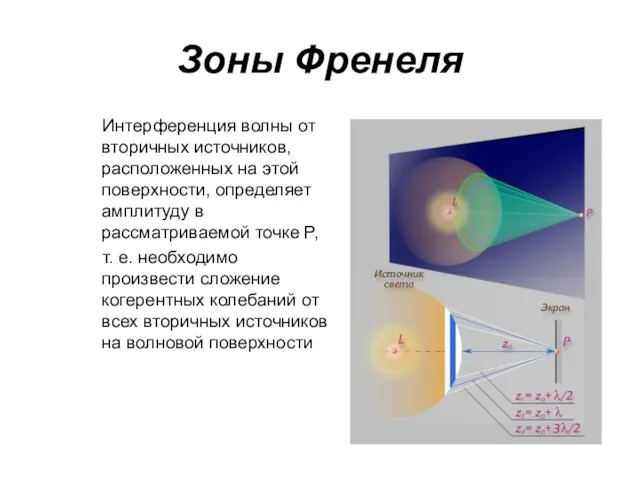
Зоны Френеля
Интерференция волны от вторичных источников, расположенных на этой поверхности, определяет амплитуду в рассматриваемой точке P,
т. е. необходимо произвести сложение когерентных колебаний от всех вторичных источников на волновой поверхности

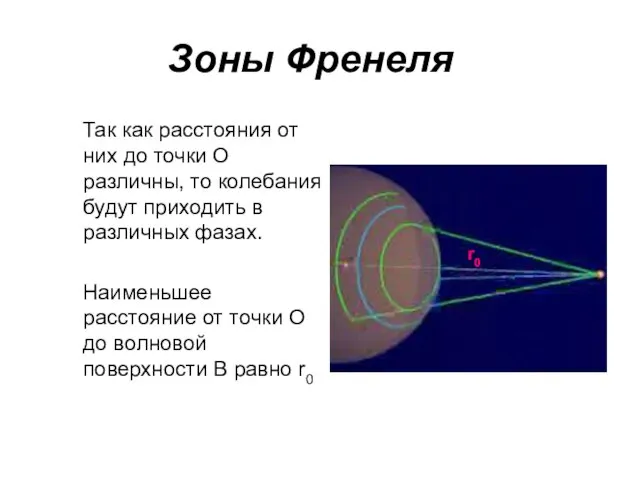
Зоны Френеля
Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах.
Наименьшее расстояние от точки О до волновой поверхности В равно r0
r0

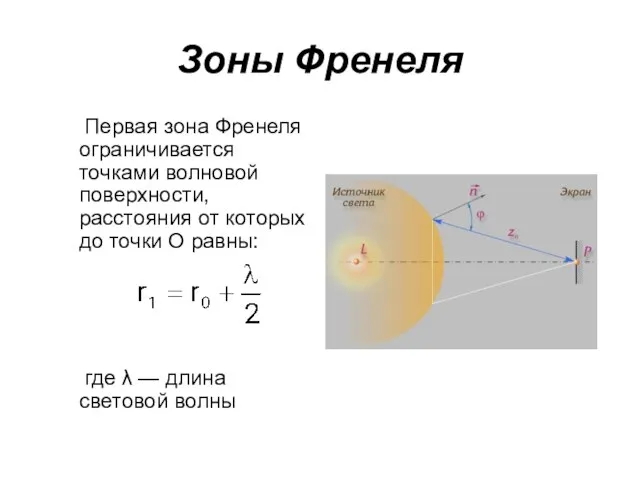
Зоны Френеля
Первая зона Френеля ограничивается точками волновой поверхности, расстояния от которых до точки О равны:
где λ — длина световой волны

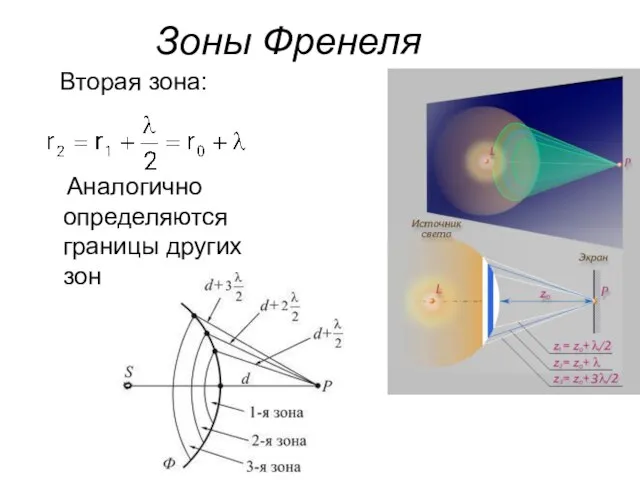
Зоны Френеля
Вторая зона:
Аналогично определяются границы других зон

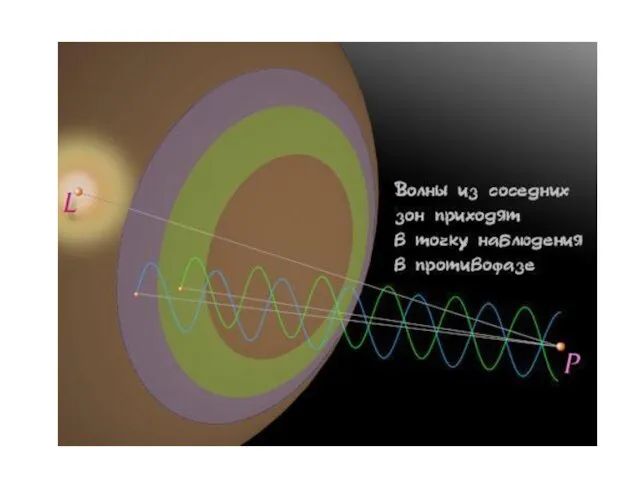
Если разность хода от двух соседних зон равна половине длины волны, то колебания от них приходят в точку О в противоположных фазах и наблюдается интерференционный минимум, если разность хода равна длине волны, то наблюдается интерференционный максимум

Можно показать, что при не слишком больших m площади зон Френеля приблизительно одинаковы
Радиус m-ой зоны Френеля
Угол φ также увеличивается с номером зоны m, в результате чего Аm – амплитуда колебания, возбуждаемого m-ой зоной в точке Р, монотонно убывает с ростом m (А1 > А2 > Аm).
Амплитуда А результирующего колебания в точке Р равна:
А=А1- А2+ А3 - А4 +…=0,5А1+(0,5А1- А2 +0,5А3)+( 0,5А3 - А4 +0,5А5)+…
Так как А монотонно убывает с m, то
тогда выражения в скобках равны нулю и А=А1/2
Таким образом, амплитуда, создаваемая в точке Р всей сферической волновой поверхностью пропорциональна ½ амплитуды, создаваемой одной лишь центральной зоной.

Если взять экран с отверстием, оставляющим открытым только центральную зону Френеля, амплитуда в точке Р будет равна А, т.е в 2 раза больше, чем от всей волны.
Соответственно интенсивность света I ~ А2 будет в 4 раза выше. Т.о. это алгебраическое сложение амплитуд.
Эту же задачу можно решить графическим сложением амплитуд (векторов амплитуд). Разобьем волновую поверхность на кольцевые зоны, подобные зонам Френеля, но меньшие по ширине так, чтобы разность хода от краев зоны до точки Р составляло одинаковую для всех зон малую долю λ. Так как амплитуда Аm убывает, то получается не замкнутая фигура, а спираль.
Метод сложения амплитуд
Если бы величина Аm не убывала, то был бы ноль. Если ширину кольцевых зон устремить к нулю, то в пределе получим спираль, закрученную к точке С. Колебание, возбуждаемое в точке Р всей волновой поверхностью, изображается вектором ОС. Амплитуда равна ½ амплитуды.

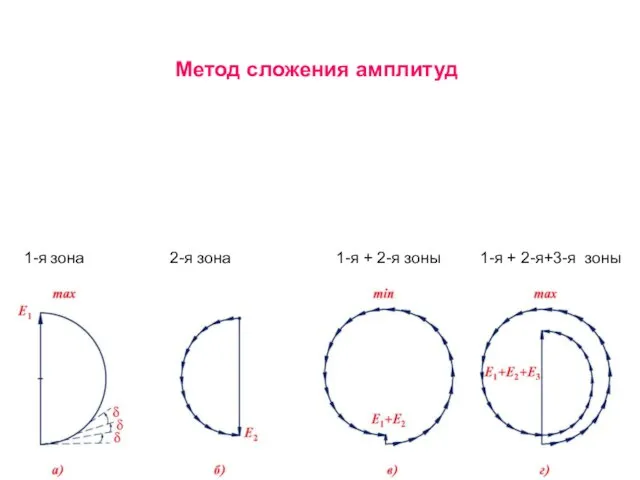
Метод сложения амплитуд
1-я зона
2-я зона
1-я + 2-я зоны
1-я + 2-я+3-я зоны

Колебания от четных и нечетных зон Френеля ослабляют друг друга (в противофазе). Если поставить на пути волны пластинку, которая перекрывала бы все четные (или нечетные) зоны, то интенсивность света в точке Р резко возрастает. Такая пластинка называется амплитудной зонной пластинкой. Еще большего (в 2 раза по амплитуде или в 4 раза по интенсивности) эффекта можно достичь не перекрывая четные зоны, а изменяя фазу их колебаний на π. Этот эффект достигается с помощью фазовой зонной пластики – прозрачной пластинки, толщина которой в местах, соответствующих четным или нечетным зонам, отличается на определенным образом подобранную величину.

Дифракция Френеля
1. Дифракция от круглого отверстия
При радиусе отверстия r0 намного меньшем, чем расстояния а до источника и b до экрана, можно считать, что а приблизительно равно расстоянию от источника до преграды, а b – расстоянию до точки Р.
Радиус m-ой зоны Френеля
Если r0 = rm, то отверстие оставит открытыми ровно m первых зон Френеля, построенных для точки Р.
Решив выражение (1) относительно m, получаем число открытых зон Френеля:
(1)

Как мы уже рассматривали, амплитуда колебания в точке Р будет равна (для m зоны): А=А1-А2+ А3 - А4 +…± Аm . Здесь Аm будет положительна, если m – нечетное, и отрицательна, при четном m. Перепишем эту формулу в виде:
А=А1/2+(А1/2- А2 +А3/2)+…
(m – нечетное)
(m – четное)
Выражения в скобках равны нулю, так как
Амплитуды от двух соседних зон мало отличаются по величине, поэтому

Итак, если m –невелико, т.е. Аm≈ А1, то А=А1/2+Аm/2 ≈ А1
А=А1/2 - Аm/2 ≈ 0
m – четное
m – нечетное
Если экран убрать, то А = А1/2
Парадокс заключается в следующем: преграда с маленьким отверстием может, в случае нечетного m увеличить интенсивность света в 4 раза (I~А2).
Но этот эффект наблюдается только в точке Р. По закону сохранения энергии, в других точках интенсивность должна уменьшиться. Т.о. отверстие действует аналогично линзе
Изменять m можно, например, передвигая экран, т.е. меняя расстояние b. Если отверстие открывает только 1 зону, на экране видно размытое светлое пятно, а чередование колец не возникает. Если открыто очень много зон, то получается геометрическая тень и только на ее краю видна дифракционная картина.

2 Дифракция от круглого диска
Если диск закрывает первые m зон Френеля, то в точке Р амплитуда световой волны
Выражения в скобках равны нулю, тогда
А= Аm+1/2
Т.о. дифракционная картина имеет вид чередующихся светлых и темных колец
Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).

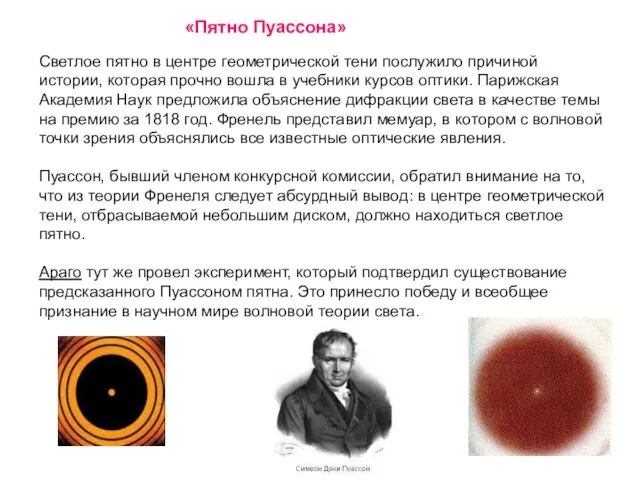
Светлое пятно в центре геометрической тени послужило причиной истории, которая прочно вошла в учебники курсов оптики. Парижская Академия Наук предложила объяснение дифракции света в качестве темы на премию за 1818 год. Френель представил мемуар, в котором с волновой точки зрения объяснялись все известные оптические явления.
Пуассон, бывший членом конкурсной комиссии, обратил внимание на то, что из теории Френеля следует абсурдный вывод: в центре геометрической тени, отбрасываемой небольшим диском, должно находиться светлое пятно.
Араго тут же провел эксперимент, который подтвердил существование предсказанного Пуассоном пятна. Это принесло победу и всеобщее признание в научном мире волновой теории света.
«Пятно Пуассона»

«Пятно Пуассона»

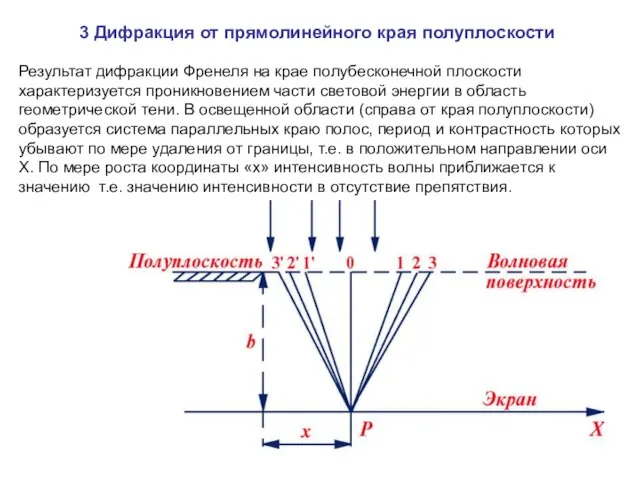
3 Дифракция от прямолинейного края полуплоскости
Результат дифракции Френеля на крае полубесконечной плоскости характеризуется проникновением части световой энергии в область геометрической тени. В освещенной области (справа от края полуплоскости) образуется система параллельных краю полос, период и контрастность которых убывают по мере удаления от границы, т.е. в положительном направлении оси Х. По мере роста координаты «х» интенсивность волны приближается к значению т.е. значению интенсивности в отсутствие препятствия.

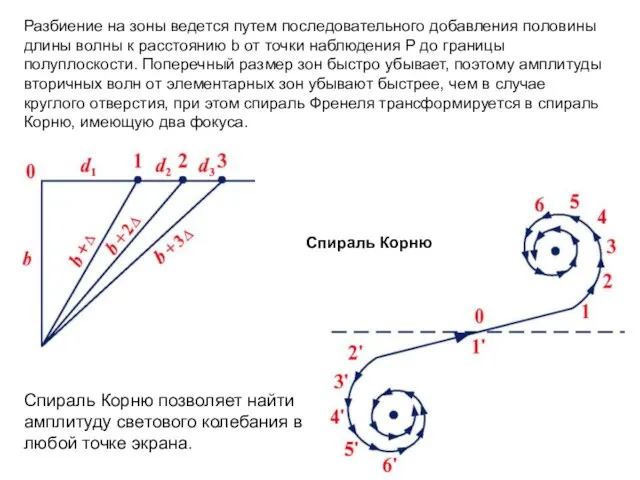
Разбиение на зоны ведется путем последовательного добавления половины длины волны к расстоянию b от точки наблюдения P до границы полуплоскости. Поперечный размер зон быстро убывает, поэтому амплитуды вторичных волн от элементарных зон убывают быстрее, чем в случае круглого отверстия, при этом спираль Френеля трансформируется в спираль Корню, имеющую два фокуса.
Спираль Корню
Спираль Корню позволяет найти амплитуду светового колебания в любой точке экрана.

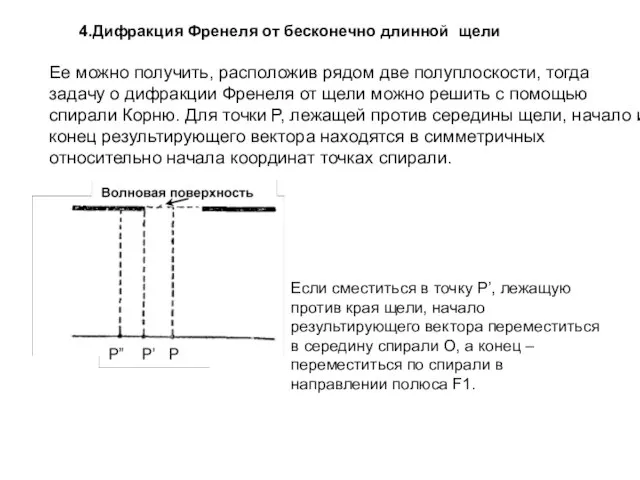
Ее можно получить, расположив рядом две полуплоскости, тогда задачу о дифракции Френеля от щели можно решить с помощью спирали Корню. Для точки Р, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали.
4.Дифракция Френеля от бесконечно длинной щели
Если сместиться в точку Р’, лежащую против края щели, начало результирующего вектора переместиться в середину спирали О, а конец –переместиться по спирали в направлении полюса F1.

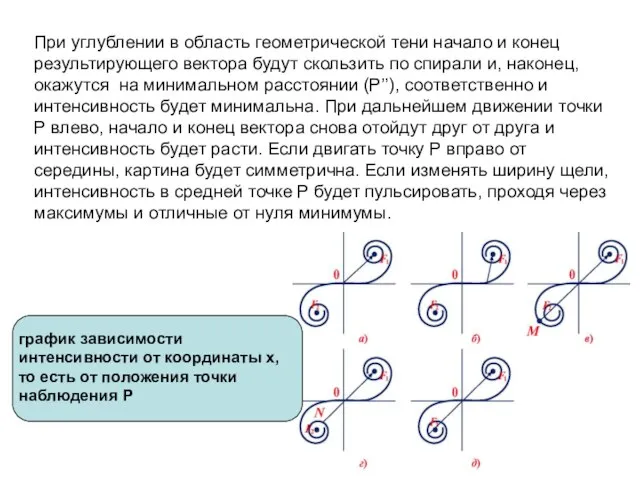
При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и, наконец, окажутся на минимальном расстоянии (Р’’), соответственно и интенсивность будет минимальна. При дальнейшем движении точки Р влево, начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. Если двигать точку Р вправо от середины, картина будет симметрична. Если изменять ширину щели, интенсивность в средней точке Р будет пульсировать, проходя через максимумы и отличные от нуля минимумы.
график зависимости интенсивности от координаты х, то есть от положения точки наблюдения P

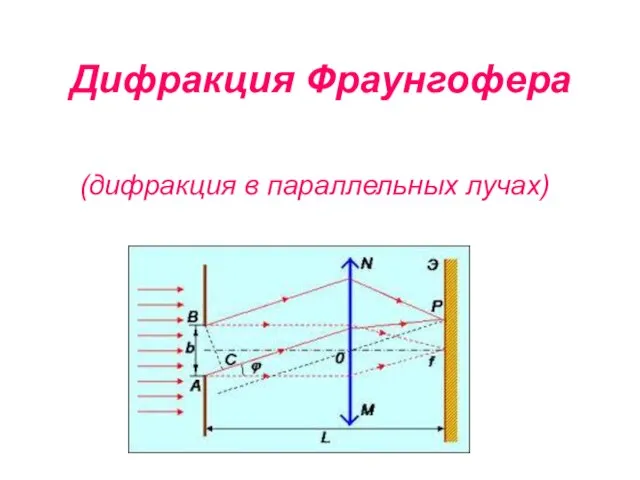
Дифракция Фраунгофера
(дифракция в параллельных лучах)

Дифракция Фраунгофера от бесконечно длинной щели
При перпендикулярном падении света на плоскость щели все точки фронта волны АВ колеблются в одной фазе. Разность хода Δ между крайними лучами пучка равна нулю. Лучи, собранные линзой в точке О, интерферируя друг с другом, взаимно усиливаются, и в этой точке получится максимум освещенности. В другой точке O1, где соберутся лучи, идущие из разных точек щели под углом φ1 к основному направлению, результат интерференции будет иной.
Очевидно, Δ = bsin φ, где b — ширина щели. Допустим, Δ = 2λ/2. Тогда рассматриваемый под углом φ1 , пучок лучей можно разделить на две части, или, как говорят, зоны, причем каждый луч i верхней зоны будет на λ/2 отставать от соответствующего луча j нижней зоны, следовательно, в точке О1 они «погасят» друг друга. Таким образом, под углом φ1, удовлетворяющим условию Δ1 = bsin φ1 = λ, происходит взаимное гашение лучей, прошедших через щель и собранных в точке O1.
Такое разделение пучка лучей или световой волны на части, которые при интерференции взаимно гасят друг друга, как уже говорилось ранее, называется разделением на зоны Френеля.

Дифракция Фраунгофера от бесконечно длинной щели
Рассмотрим другое направление — под углом φ2, для которого Δ2 = bsinφ2 = 3λ/2. В этом направлении пучок света можно разделить на три зоны из которых две зоны (первая и вторая или вторая и третья) друг друга погасят, а третья останется непогашенной и даст в соответствующей точке экрана О2 некоторую освещенность, которая будет значительно меньше, чем освещенность в точке О.
Рассуждая таким образом, можно показать, что в направлениях, в которых bsinφ равно нулю или нечетному числу λ/2 и, следовательно, пучок света состоит из нечетного числа зон Френеля (1, 3, 5 и т. д.), на экране получаются светлые точки (вернее, линии, параллельные щели), а в направлениях, для которых bsinφ равно четному числу λ/2 и, следовательно, пучок света делится на четное число взаимно гасящих друг друга зон, на экране получаются темные линии. В промежуточных направлениях освещенность экрана постепенно уменьшается от нуля до соответствующих максимумов.
Распределение освещенности на экране (расположенном в фокальной плоскости линзы), полученное вследствие дифракции световой волны, называется дифракционным спектром.

Дифракция Фраунгофера от бесконечно длинной щели
Так как углы φ очень малы, то sinφ ≈φ и условия максимума выполняются под углами: Δ = bsin φ = (2k+1) λ/2,
φ ≈ (2k+1) λ/2b, (так как φ мал, иначе интенсивность максимума убывает, то λ≈2b, т.е. b должно быть сравнимо с длиной волны),
а условия минимума — под углами:
φ ≈ 2k•λ/2b = k•λ/b (k = 1, 2, 3, ...).
Чем уже щель, тем дальше друг от друга располагаются максимумы. Расположение максимумов и минимумов зависит от длины
Расположение максимумов и минимумов зависит от длины волны света. Если падающий свет — сложный, например, белый то на экране максимумы и минимумы для различных цветов располагаются в различных местах.

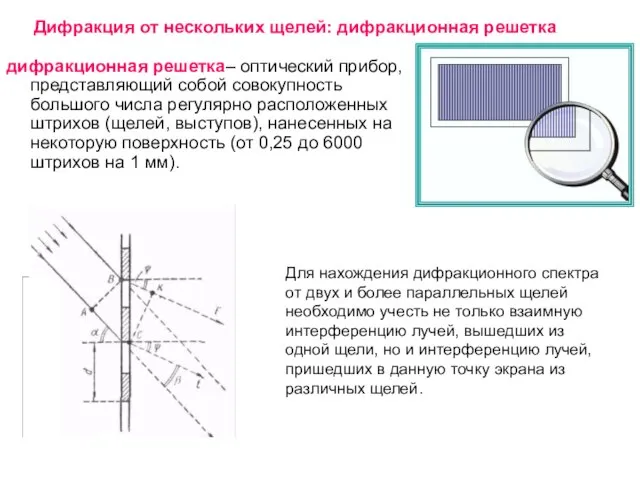
Дифракция от нескольких щелей: дифракционная решетка
дифракционная решетка– оптический прибор, представляющий собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесенных на некоторую поверхность (от 0,25 до 6000 штрихов на 1 мм).
Для нахождения дифракционного спектра от двух и более параллельных щелей необходимо учесть не только взаимную интерференцию лучей, вышедших из одной щели, но и интерференцию лучей, пришедших в данную точку экрана из различных щелей.

Дифракционная решетка
Величина d = a + b называется постоянной (периодом) дифракционной решетки, где а — ширина щели; b — ширина непрозрачной части

Дифракция от нескольких щелей: дифракционная решетка
Каждая щель дает на экране ту или иную освещенность по всем направлениям, кроме тех, которые удовлетворяют условиям гашения:
bsin φ =λ, 2λ, 3λ,…; φ ≈ k·λ/b
В этих направлениях условия гашения (четное число зон Френеля) выполняются для каждой щели в отдельности.
Рассмотрим некоторое направление под углом ψ и допустим, что первая щель посылает свет, интенсивность которого в соответствующей точке экрана определяется вектором Е1, вторая щель дает Е2, третья — Е3 и т. д. В точке М, где собираются лучи от всех щелей, освещенность определяется значением суммарного вектора Е = E1+ Е2+ Е3 + .... Рассмотрим два наиболее простых случая:

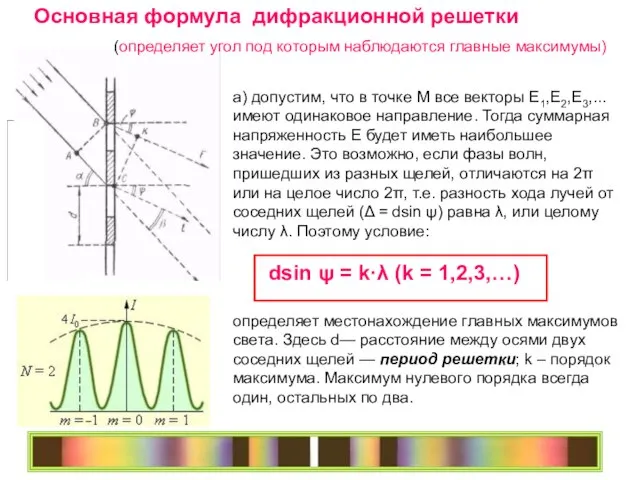
а) допустим, что в точке М все векторы Е1,Е2,Е3,... имеют одинаковое направление. Тогда суммарная напряженность Е будет иметь наибольшее значение. Это возможно, если фазы волн, пришедших из разных щелей, отличаются на 2π или на целое число 2π, т.е. разность хода лучей от соседних щелей (Δ = dsin ψ) равна λ, или целому числу λ. Поэтому условие:
dsin ψ = k·λ (k = 1,2,3,…)
определяет местонахождение главных максимумов света. Здесь d— расстояние между осями двух соседних щелей — период решетки; k – порядок максимума. Максимум нулевого порядка всегда один, остальных по два.
Основная формула дифракционной решетки
(определяет угол под которым наблюдаются главные максимумы)

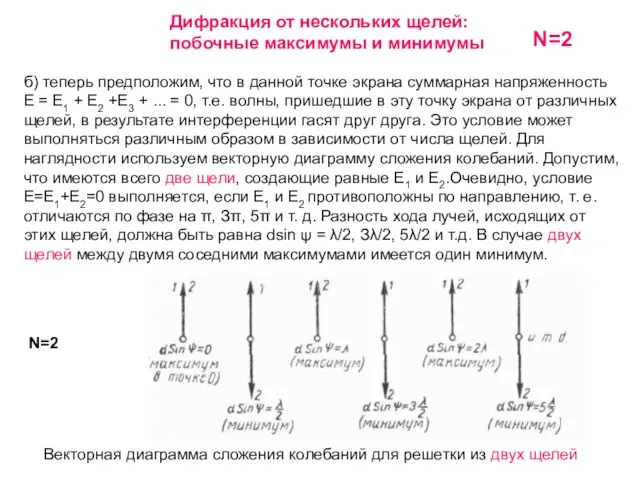
б) теперь предположим, что в данной точке экрана суммарная напряженность Е = Е1 + Е2 +Е3 + ... = 0, т.е. волны, пришедшие в эту точку экрана от различных щелей, в результате интерференции гасят друг друга. Это условие может выполняться различным образом в зависимости от числа щелей. Для наглядности используем векторную диаграмму сложения колебаний. Допустим, что имеются всего две щели, создающие равные E1 и Е2.Очевидно, условие Е=E1+Е2=0 выполняется, если E1 и Е2 противоположны по направлению, т. е. отличаются по фазе на π, Зπ, 5π и т. д. Разность хода лучей, исходящих от этих щелей, должна быть равна dsin ψ = λ/2, Зλ/2, 5λ/2 и т.д. В случае двух щелей между двумя соседними максимумами имеется один минимум.
Векторная диаграмма сложения колебаний для решетки из двух щелей
Дифракция от нескольких щелей:
побочные максимумы и минимумы
N=2
N=2

Дифракция от нескольких щелей:
побочные максимумы и минимумы
В случае трех щелей для получения максимумов по-прежнему считаем, что все векторы E1, Е2, Е3 имеют одинаковое направление и складываются; для получения же минимума, в частности для равенства E1+Е2+Е3=0, необходимо, чтобы фазы этих векторов отличались либо на 2π/3 (120° или λ/3), либо на 2•2π/3 (240° или 2λ/3). При наличии трех щелей между двумя соседними максимумами появляются два минимума.
N=2
Векторная диаграмма сложения колебаний для решетки из трех щелей
N=3

Дифракция от нескольких щелей:
побочные максимумы и минимумы
N=4
Для четырех щелей условия минимума имеют место, если разность фаз между векторами напряженностей от соседних щелей равна π/2, 2π/2, Зπ/2, а разность хода — λ/4, 2λ/4, Зλ/4 и т. д.
При наличии четырех щелей между двумя соседними максимумами образуются три минимума.
Продолжая рассуждения, можно установить следующее правило:
при наличии N щелей между двумя соседними максимумами образуются N — 1 минимумов; разность хода лучей dsin ψ от двух соседних щелей для максимумов должна равняться целому числу λ, а для минимумов; λ/N, 2λ/N, 3λ/N и т. д. Дополнительные (побочные) максимумы, расположенные между двумя соседними минимумами, создают на экране весьма слабую освещенность (фон).