Dimensions and Units

Announcement
Required Project Meeting
for all Physics students:
Wednesday, 1st October, 2014 @ 4 pm
Senate Hall Block 1, 3rd floor
Bring a notebook. Be on time.

1. Definitions
Oxford English Dictionary: Physics: ‘Science dealing with properties and interactions of matter and energy’;
Physics (from the Greek words natural and nature) is the science of the natural world. It studies the fundamental constituents of the universe, the forces they exert on one another, and the results produced by these forces;
Galileo (1623): “The book of Nature is written in the language of Mathematics”. Mathematics is essential to understanding Physics
http://www.youtube.com/watch?v=6hnvLCkCiU8

Objectives of Physics
To find the limited number of fundamental laws that govern natural phenomena;
To use these laws to develop theories that can predict and explain the results of future experiments or actions;
To find mathematical expressions for these laws;
Theory and Experiments should complement each other.

Classical Physics
Includes principles developed mainly before 1900;
Mechanics: major developments by Newton, and continuing throughout the 18th century;
Thermodynamics, optics and electromagnetism: developed
in the 2nd half of the 19th century

Modern Physics
Deals with phenomena that could not be explained by Classical Physics;
Special Relativity: explains the behaviour of objects near the speed of light. Modifies the traditional concepts of space, time, mass, and energy;
Quantum Physics: describes
physical phenomena at the
atomic level

2. Measurements and Units
Physics is quantitative: define variables, symbols or physical quantities, and their units;
Find relations between variables;
Measure these variables;
Our measurements must yield the same results when performed by anyone, anywhere and cannot change with time; we need a standard system of units!
Système International (SI): agreed in 1960 by an International Committee, is currently used by almost all the countries in the world.

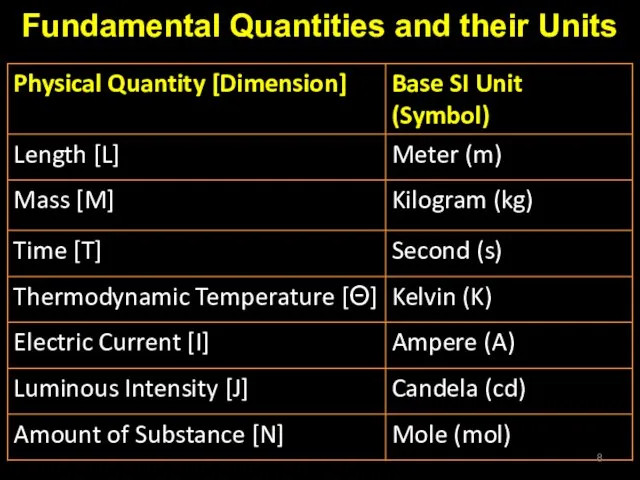
Fundamental Quantities and their Units

Base units
All Physical quantities can be expressed in one of the seven base units;
The metre has been redefined most recently, as the distance travelled by light, in vacuum, in a time interval of 1/299792458 of a second;

The most recent definition of the second is based on the high precision of atomic clocks running on Cesium-133;
The kilogram is the mass of a specific platinum-iridium alloy cylinder kept at the International Bureau of Weights and Measures, somewhere in France.

Example 1. Base and Derived Units
Find the Newton (N) in terms of the base units. Note: The Newton is an example of a derived unit.

3. Dimensional Analysis
Dimension denotes the physical nature of a quantity;
The square brackets indicate the dimensions of a physical quantity: e.g. [L] for Length, [T] for Time or [M] for Mass;
Dimensional Analysis is a technique used to check the validity of an equation or to derive it. This technique is possible because the dimensions obey basic algebraic rules;
Both sides of an equation MUST have the same dimensions for the equation to be valid.

Dimensional Homogeneity and Validity
Note: if an equation is homogeneous, it only means that the equation could be correct
E.g., mv2 gives the correct units of energy for Kinetic Energy, but the “½” term is necessary to obtain the correct form of KE = ½ mv2
Homogeneous equation: [LHS] = [RHS]
Valid equation: LHS = RHS

Example 2. Dimensional Analysis
The thrust, F, on a rocket depends on the cross-sectional area of the jet, A, the density, ρ, of the gas mixture, and the velocity, v, of the ejection. Which of the following formulae is possible if k is a dimensionless constant?
a) F = kAρv b) F = kAρv2 c) F = kA2ρv2

Example 3. Dimensional Analysis
Given that the period T of a simple pendulum depends on its length L and the acceleration due to gravity, g, find an expression for T as a function of L and g.

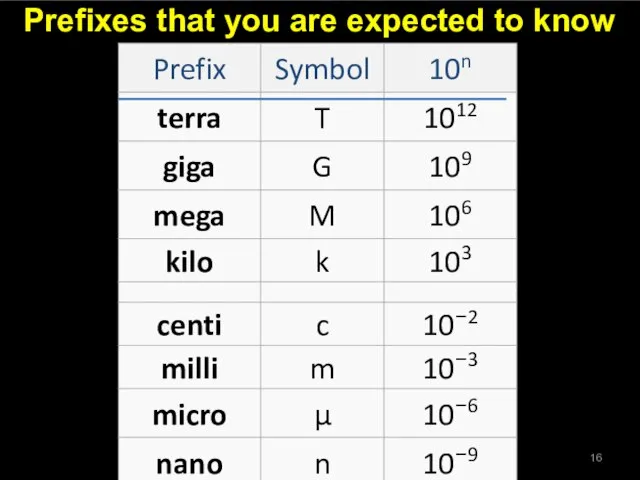
Prefixes that you are expected to know

4. Uncertainty and Significant Figures
Physical quantities cannot be measured with total accuracy and utmost confidence due to measurement uncertainties;
The order of magnitude is an approximation;
Thus not all the digits of a measured quantity are reliable;
A significant figure is a digit that is known with great confidence.

Significant Figures
Zeroes may or may not be significant; those used to locate the decimal point are not significant, e.g. 0.1 or 0.01 or 0.000…0001 all have one significant figure;
Use scientific notation to determine the number of significant figures correctly, e.g. 1.0×10-1, 1.05×10-2, etc.
The number of decimal places does not always equal the number of significant figures!

Significant Figures (Sig. Figs.) - Examples
0.0075 m has 4 decimal places but only 2 significant figures, because it is equivalent to 7.5 × 10-3 m;
10.0 m has 3 significant figures, as the decimal point gives information about the reliability of the measurement;
1500 m is ambiguous, but 1 and 5 are significant
1.5 × 103 m has 2 significant figures
1.50 × 103 m has 3 significant figures
1.500 × 103 m has 4 significant figures

Significant Figures in Calculations
The smallest number of decimal places prevails in additions and subtractions;
Example: the result of 135 cm + 3.25 cm should be written as 138 cm
The lowest number of significant figures prevails in multiplications and divisions.
Example: the result of 25.57 m × 2.45 m should be written as 62.7 m2
In general, we will not exceed 3 sig. figs. in this course.

Rounding Sig. Figs.
Is the last dropped digit < 5 or ≥ 5 ?
Drop it if it is < 5;
If it is ≥ 5, then raise the last retained digit by one.
Example: 2.349 rounds down to 2.3 if only two Sig. Figs. are allowed, but rounds up to 2.35 when three Sig. Figs. are allowed.
Read more about this in Chapter 1.4 in your Essentials of College Physics Textbook by Serway & Vuille

Intermediate Steps
General rule for calculations involving multiple steps (this course only!): the Sig. Fig. and rounding rules apply only to final and reported intermediate results. Use as many digits as your calculator allows you for the rest of the intermediate (unreported) values.