Содержание
- 2. Цель лекции Изучить базовые идеи динамического программирования и простейшие примеры его применения Изучить методы реализации этих
- 3. Чем не является динамическое программирование Динамическое программирование – не метод составления программ, а метод составления алгоритмов
- 4. Где используется динамическое программирование? Алгоритм обработки графов Алгоритмы обработки строк Биоинформатика Распознавание речи Оптимизация запросов к
- 5. Числа Фибоначчи Пример почти динамического программирования Fib(0) = Fib(1) = 1 Fib(n) = Fib(n-1) + Fib(n-2),
- 6. Простой способ вычисления function fib(n : longint) : longint; begin if (n result := 1; exit;
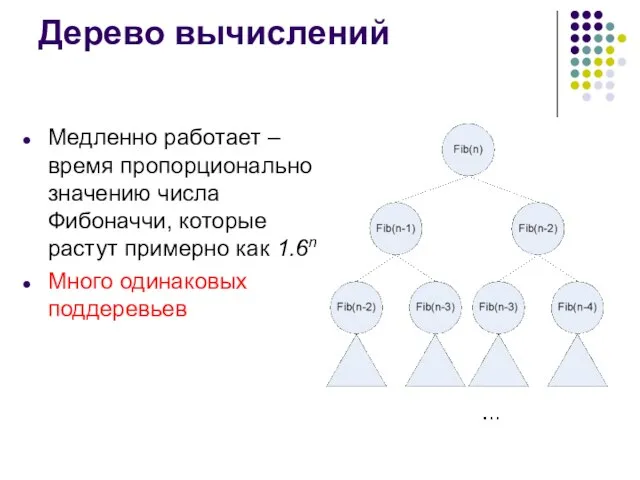
- 7. Дерево вычислений Медленно работает – время пропорционально значению числа Фибоначчи, которые растут примерно как 1.6n Много
- 8. Метод запоминания ответов После того, как число вычислено надо его запомнить, а не считать заново В
- 9. Более быстрое вычисление function fib(n : longint) : longint; begin if (n result := 1; exit;
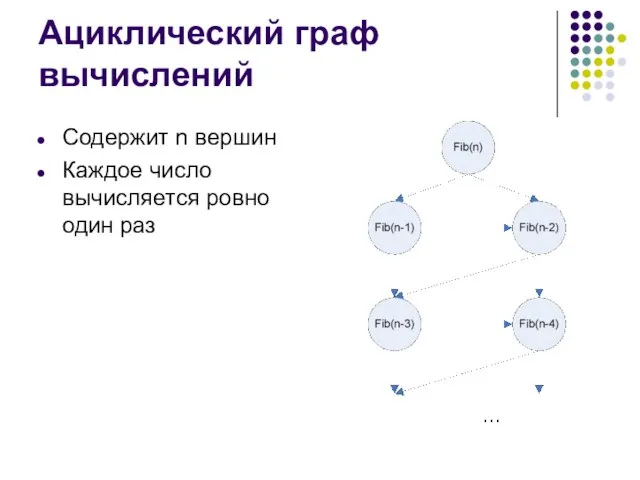
- 10. Ациклический граф вычислений Содержит n вершин Каждое число вычисляется ровно один раз
- 11. Что позволило ускорить вычисление? Перекрывающиеся подзадачи (много одинаковых поддеревьев) Небольшое число различных подзадач (для вычисления Fib(n)
- 12. Признаки возможности применения ДП Возможность разбиения задачи на подзадачи (метод «разделяй-и-властвуй») Наличие свойства оптимальности для подзадач
- 13. Этапы решения задачи методом динамического программирования Разбиение задачи на подзадачи Построение рекуррентной формулы для вычисления значения
- 14. Задача о наибольшей общей подпоследовательности На примере этой задачи будут рассматриваться указанные четыре этапа На базе
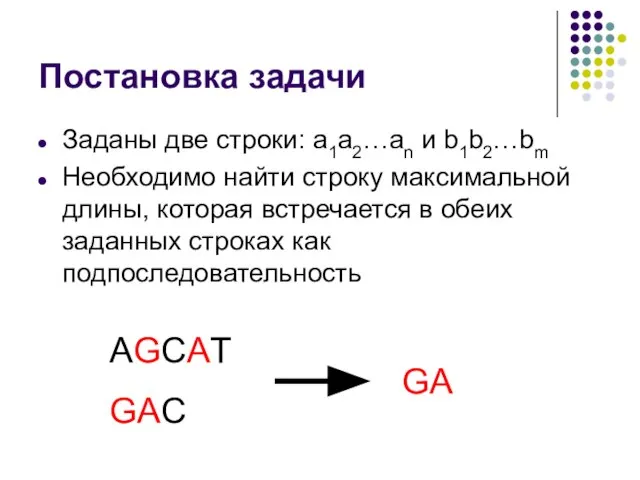
- 15. Постановка задачи Заданы две строки: a1a2…an и b1b2…bm Необходимо найти строку максимальной длины, которая встречается в
- 16. Медленное решение Перебрать все подпоследовательности одной из строк и проверить их вхождение в другую строку Число
- 17. Разбиение на подзадачи (1) Рассмотрим строки : a1a2…an и b1b2…bm Если последние символы совпадают (an=bm), то
- 18. Разбиение на подзадачи (2) Подзадачами являются задачи такого типа «Найти наибольшую общую подпоследвательность строк a1a2…ai и
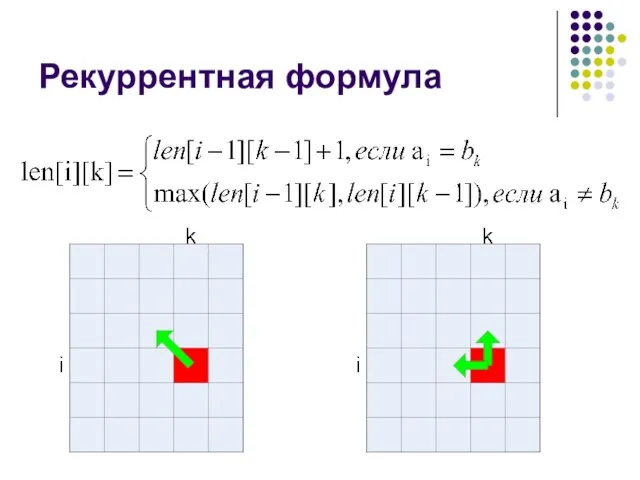
- 19. Рекуррентная формула
- 20. Начальные условия len[0][k] = 0 для всех k len[i][0] = 0 для всех i
- 21. Два метода вычисления «Сверху вниз» – рекурсия с запоминанием ответов «Снизу вверх» – заполнение таблицы
- 22. Метод «сверху вниз» Решение больших подзадач начинается до того, как получены ответы для маленьких Маленькие решаются
- 23. Программа function calc(i, k : integer) : integer; begin if (calculated[i][k]) then begin result := len[i][k];
- 24. Преимущества и недостатки Преимущества: Достаточно просто пишется на основе рекуррентной формулы Вычисляются ответы только для тех
- 25. Метод «снизу вверх» Заполняется таблица ответов на подзадачи в порядке возрастания размера подзадачи Когда начинается решение
- 26. Программа len[0][0] := 0; for i := 1 to n do begin len[i][0] := 0; end;
- 27. Преимущества и недостатки Преимущества: Требуется меньше памяти, чем при методе «сверху вниз» и отсутствует рекурсия Быстрее
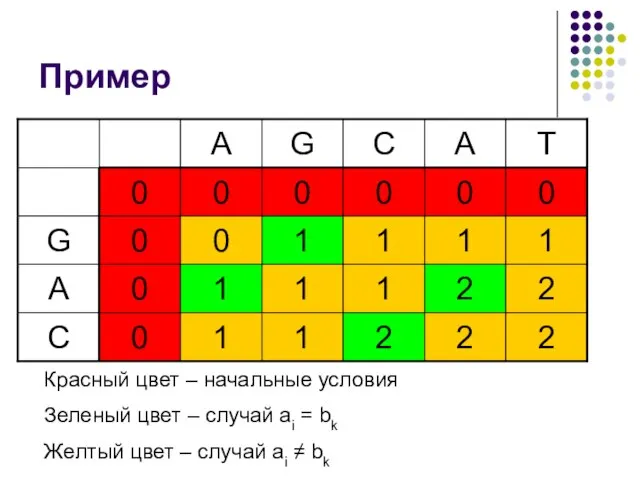
- 28. Пример Красный цвет – начальные условия Зеленый цвет – случай ai = bk Желтый цвет –
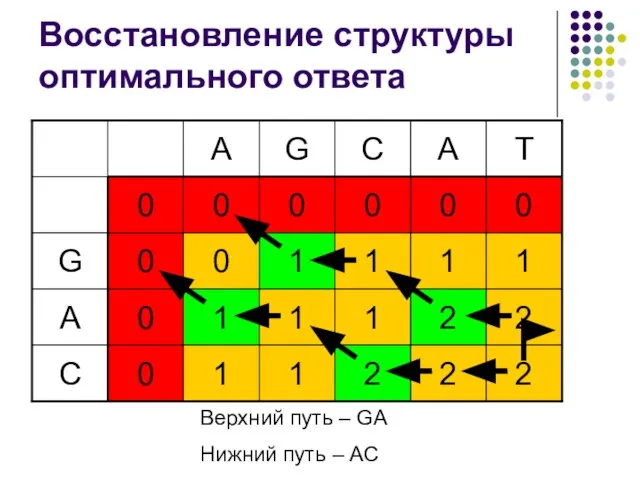
- 29. Восстановление структуры оптимального ответа Верхний путь – GA Нижний путь – AC
- 30. Программа procedure restore(i, k : integer); begin if (i = 0) or (k = 0) then
- 31. Как делать в общем случае? Такой метод работает в этой задаче, но не понятно, как его
- 32. Вычисление функции с запоминанием выбранного варианта for i := 1 to n do begin for k
- 33. Восстановление ответа procedure restore(i, k : integer); begin if (i = 0) or (k = 0)
- 34. Упражнение – 1 Путь с максимальной суммой. Задан прямоугольник размером n на m, в каждой клетке
- 35. Упражнение – 2 Число путей. Задан прямоугольник размером n на m, некоторые клетки которого вырезаны. За
- 36. Упражнение – 3 Максимальный подпалиндром. Задана строка. Необходимо найти наибольшую по длине подпоследовательность, которая является палиндромом
- 37. Упражнение – 4 Наибольшая возрастающая подпоследовательность. Задана последовательность из n чисел. Необходимо найти ее наибольшую по
- 38. Литература Кормен, Лейзерсон, Ривест, Штайн «Алгоритмы. Построение и анализ», глава 15
- 39. Выводы Динамическое программирование – метод составления алгоритмов Оно применимо в случае наличия перекрывающихся подзадач Решение задачи
- 41. Скачать презентацию














![Начальные условия len[0][k] = 0 для всех k len[i][0] = 0 для всех i](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/388374/slide-19.jpg)


![Программа function calc(i, k : integer) : integer; begin if (calculated[i][k]) then](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/388374/slide-22.jpg)


![Программа len[0][0] := 0; for i := 1 to n do begin](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/388374/slide-25.jpg)











 Спиридон Дмитриевич Дрожжин
Спиридон Дмитриевич Дрожжин Презентация на тему Солнце и звёзды
Презентация на тему Солнце и звёзды  A walk down by the river Thames
A walk down by the river Thames Моторика обучения игры в баскетбол
Моторика обучения игры в баскетбол ПРАВИЛА ЗАПИСИ АРИФМЕТИЧЕСКИХ ВЫРАЖЕНИЙ
ПРАВИЛА ЗАПИСИ АРИФМЕТИЧЕСКИХ ВЫРАЖЕНИЙ Диагностика отклонений в развитии
Диагностика отклонений в развитии Художник в цирке
Художник в цирке Моторика обучения игры в баскетбол
Моторика обучения игры в баскетбол Схема замещения трансформатора и ее параметры
Схема замещения трансформатора и ее параметры Международный день защиты детей
Международный день защиты детей ГБОУ детский сад № 806 представляет проект: «Матвеевское: вчера, сегодня, завтра»
ГБОУ детский сад № 806 представляет проект: «Матвеевское: вчера, сегодня, завтра» Химия и живой организм
Химия и живой организм АРТ-терапия
АРТ-терапия Русская архитектура первой половины 19 века
Русская архитектура первой половины 19 века Принципы успешной защиты курсовой работы
Принципы успешной защиты курсовой работы 20141117_mineralnye_resursy_8_klass
20141117_mineralnye_resursy_8_klass МОСКВА – ТРЕТИЙ РИМ
МОСКВА – ТРЕТИЙ РИМ  «Единственная» - любимый журнал украинских женщин! Целевая аудитория: женщины, возраст 18 - 45 лет, достаток «средний+» Тираж номера: 20
«Единственная» - любимый журнал украинских женщин! Целевая аудитория: женщины, возраст 18 - 45 лет, достаток «средний+» Тираж номера: 20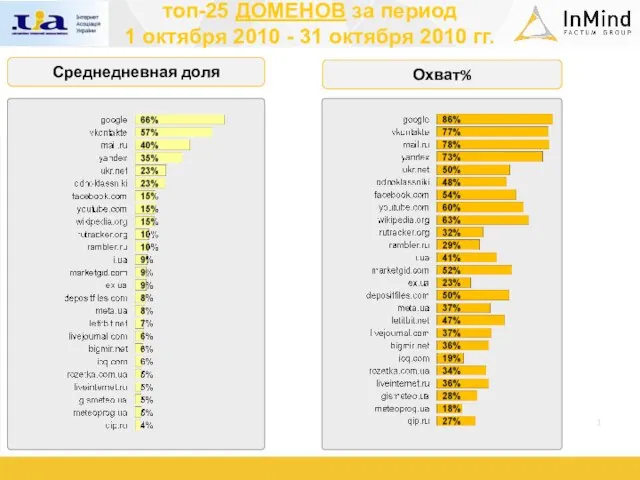 топ-25 ДОМЕНОВ за период 1 октября 2010 - 31 октября 2010 гг.
топ-25 ДОМЕНОВ за период 1 октября 2010 - 31 октября 2010 гг. Культура Киевской Руси
Культура Киевской Руси Матрица “IS”
Матрица “IS” for MVIDEO
for MVIDEO Основная образовательная программа образовательного учреждения – важнейший стратегический документ
Основная образовательная программа образовательного учреждения – важнейший стратегический документ Районный конкурс Новогодний серпантин. Номинация Оформление интерьера. Украшение окна
Районный конкурс Новогодний серпантин. Номинация Оформление интерьера. Украшение окна Федеральный государственный образовательный стандарт
Федеральный государственный образовательный стандарт English proverbs and sayings with a component “pets and other animals” and their Russian equivalents
English proverbs and sayings with a component “pets and other animals” and their Russian equivalents Обжалование решений о приостановлении осуществления государственного кадастрового учета
Обжалование решений о приостановлении осуществления государственного кадастрового учета Генетически модифицированные организмы (ГМО)Данная презентация необходима для изучения раздела «Гигиеническая и экологическая
Генетически модифицированные организмы (ГМО)Данная презентация необходима для изучения раздела «Гигиеническая и экологическая