Содержание
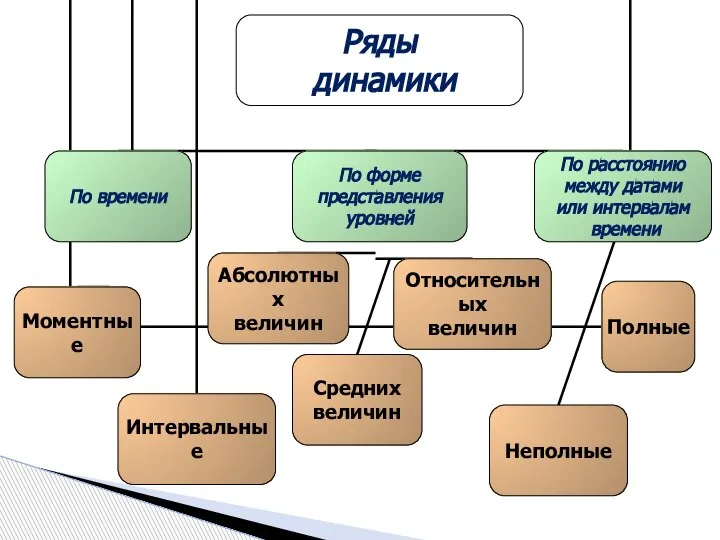
- 2. это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Ряд динамики
- 4. Примеры рядов динамики Число дошкольных учреждений в России (на конец года), тыс. Моментный Абсолютных величин Полный
- 5. Примеры рядов динамики Моментный Относительных величин Полный Уровень экономической активности населения России (на начало года), %
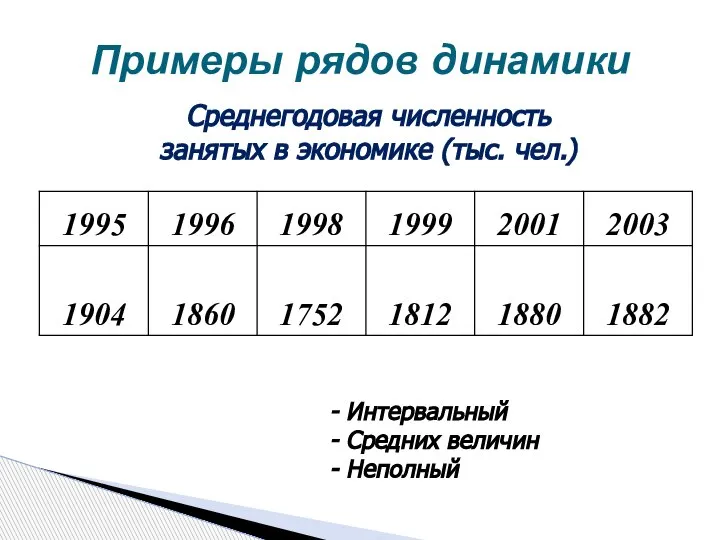
- 6. Примеры рядов динамики Интервальный Средних величин Неполный Среднегодовая численность занятых в экономике (тыс. чел.)
- 7. Сопоставимость по территории Сопоставимость по кругу охватываемых объектов Сопоставимость по единицам измерения Упорядоченность во времени Ряд
- 8. Показатели анализа рядов динамики
- 9. Показатели анализа рядов динамики
- 10. средний уровень ряда - показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся
- 11. Средний уровень ряда Для интервальных рядов с равными периодами времени Для интервального ряда с неравноотстоящими уровнями
- 12. Средний абсолютный прирост или где или Средний темп прироста Средний темп роста
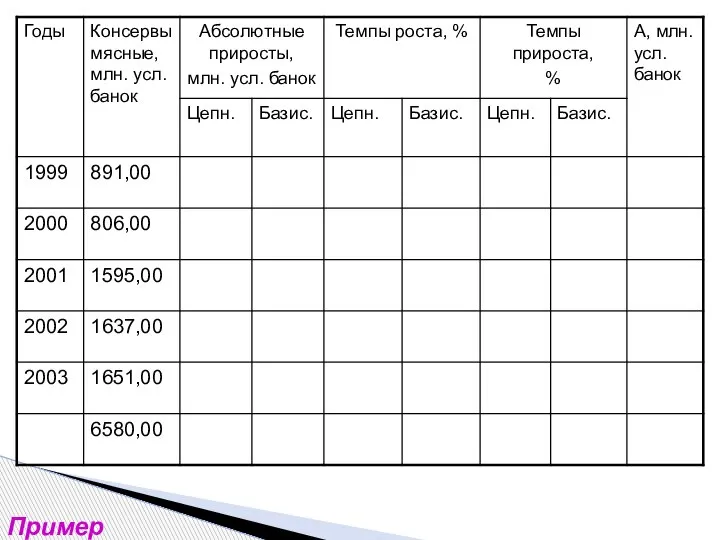
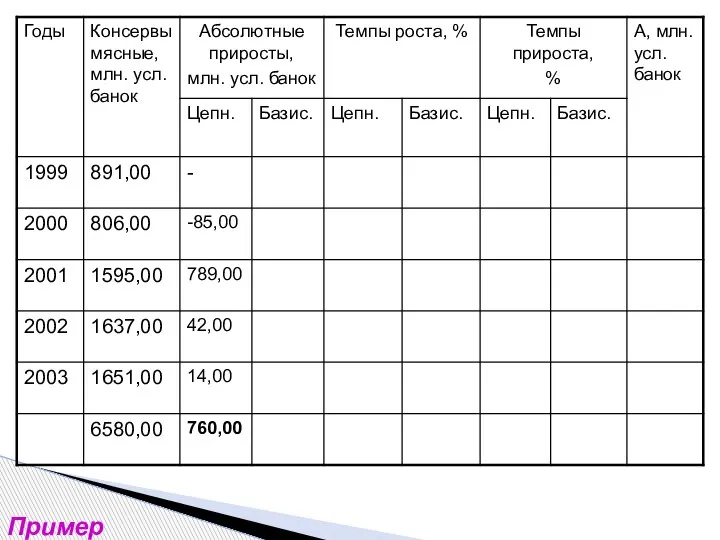
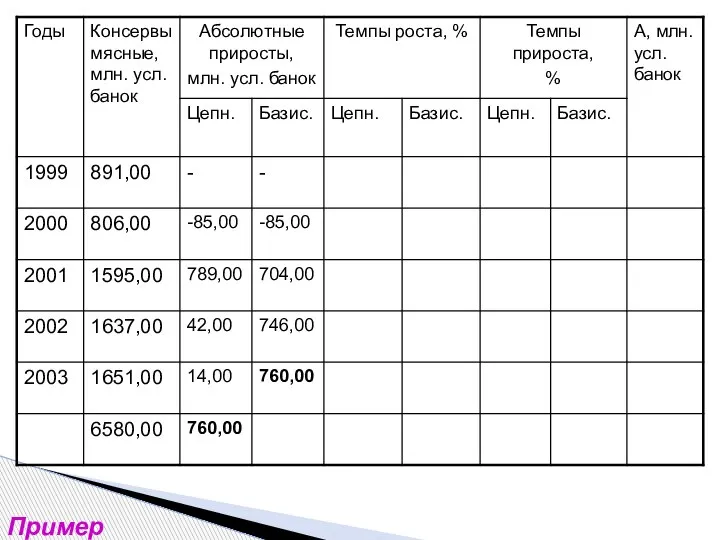
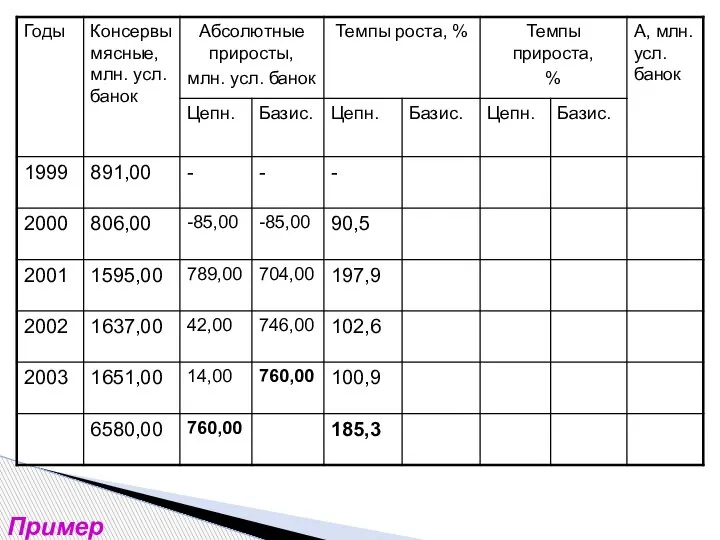
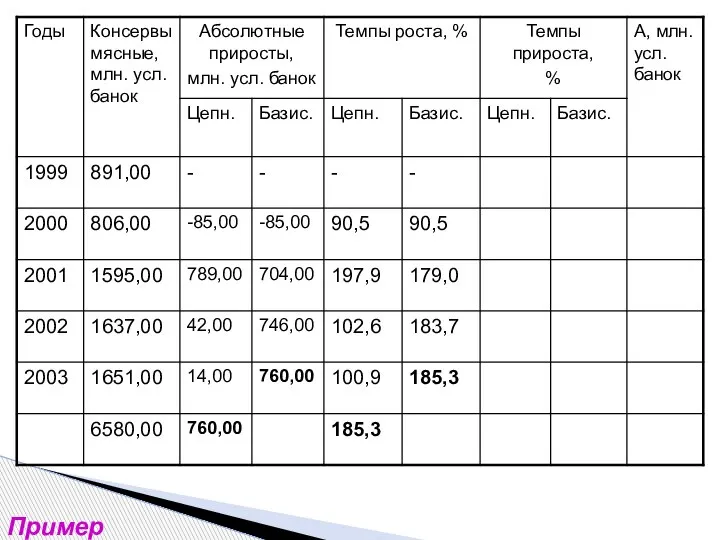
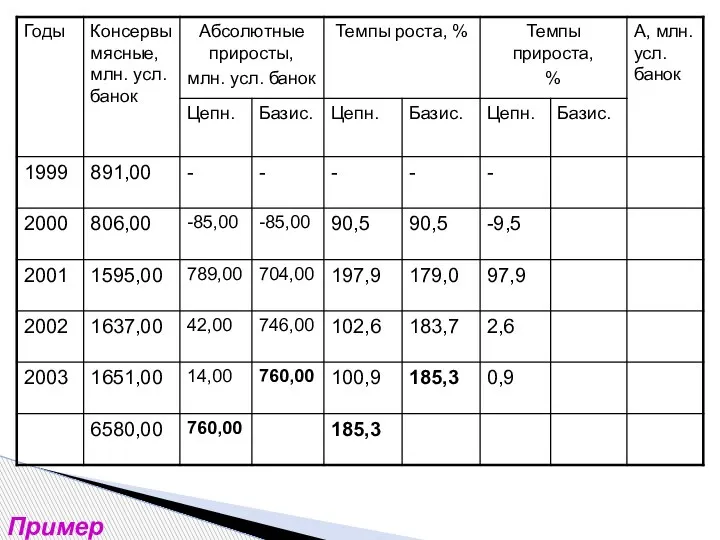
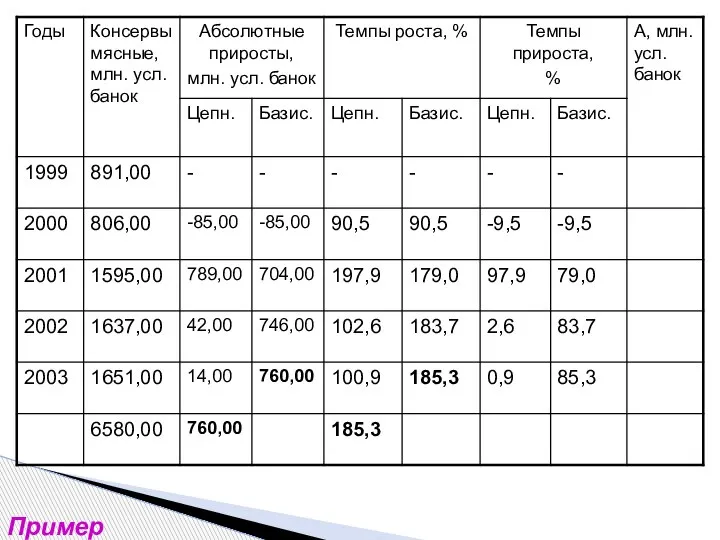
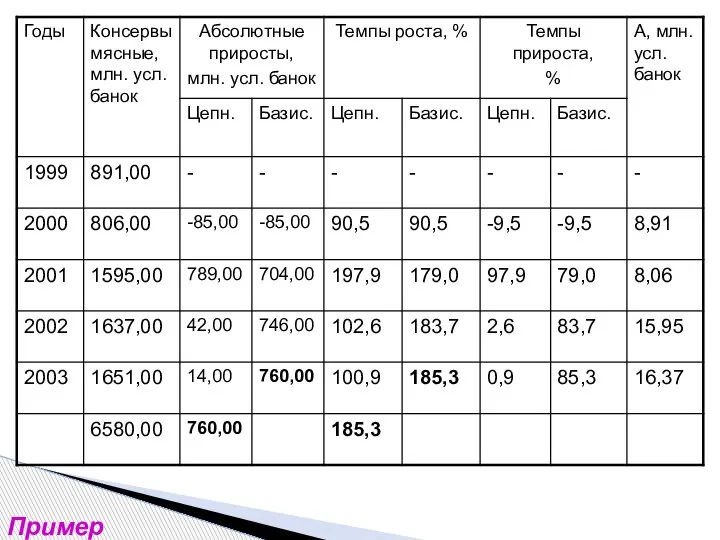
- 13. Пример
- 14. Пример
- 15. Пример
- 16. Пример
- 17. Пример
- 18. Пример
- 19. Пример
- 20. Пример
- 21. Средние Для интервальных рядов с равными периодами времени Средний абсолютный прирост Средний темп роста Средний темп
- 22. составляющие: тренд - основная тенденция развития динамического ряда (к увеличению либо снижению его уровней); циклические (периодические)
- 23. этапы: ряд динамики проверяется на наличие тренда; производится выравнивание временного ряда и непосредственное выделение тренда с
- 24. методы : Укрупнение интервалов; Скользящая средняя; Аналитическое выравнивание. Непосредственное выделение тренда
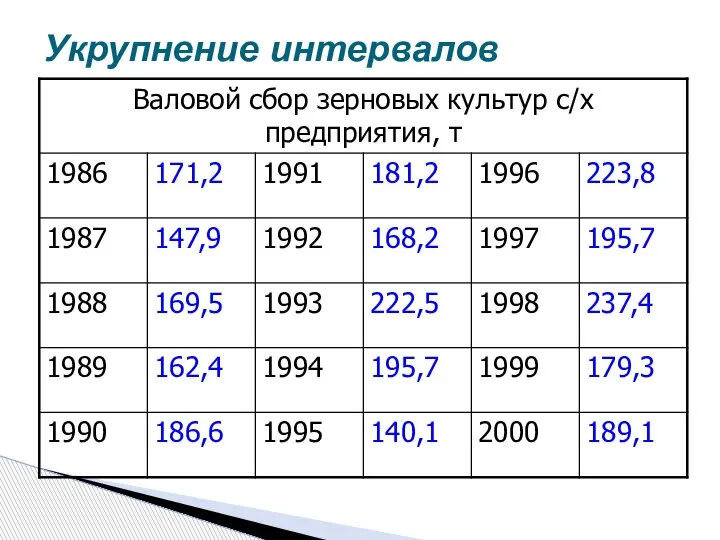
- 25. Укрупнение интервалов
- 26. Укрупнение интервалов
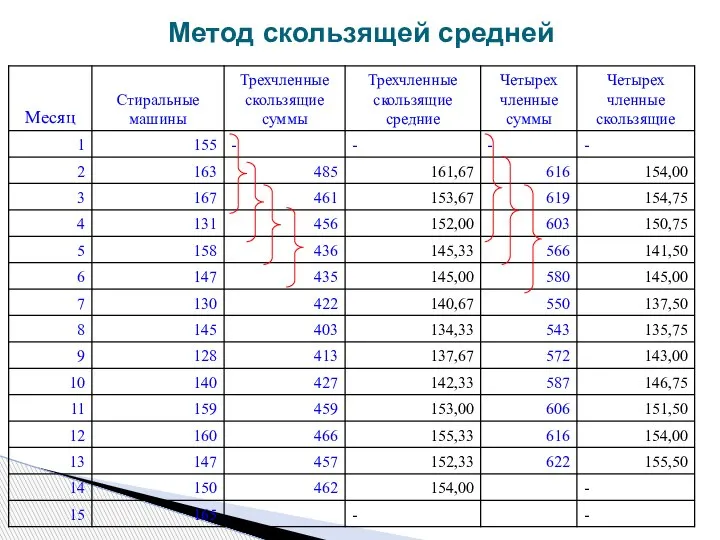
- 27. Метод скользящей средней
- 28. Аналитическое выравнивание где f(t) - уровень, определяемый тенденцией развития; εt - случайное и циклическое отклонение от
- 29. Аналитическое выравнивание
- 30. Аналитическое выравнивание Линейная зависимость - абсолютные цепные приросты, не проявляют тенденции ни к увеличению, ни к
- 31. Метод наименьших квадратов (МНК) где y – исходный уровень ряда динамики, n – число членов ряда,
- 32. Метод наименьших квадратов
- 33. Метод наименьших квадратов показатель времени t
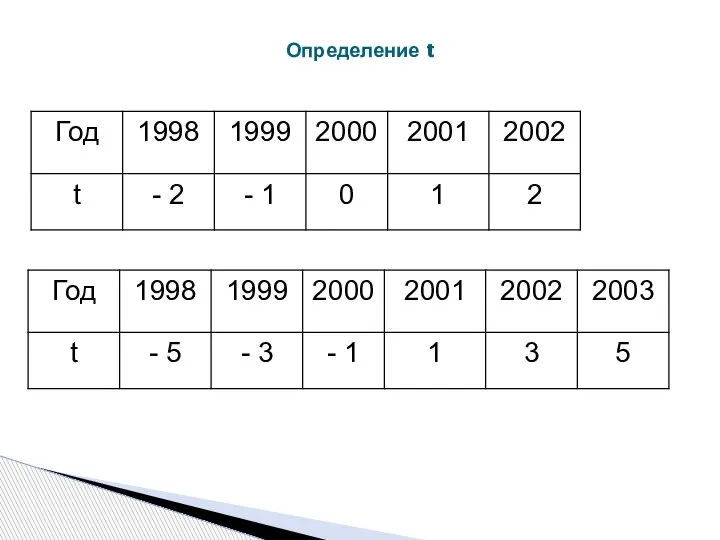
- 34. Определение t
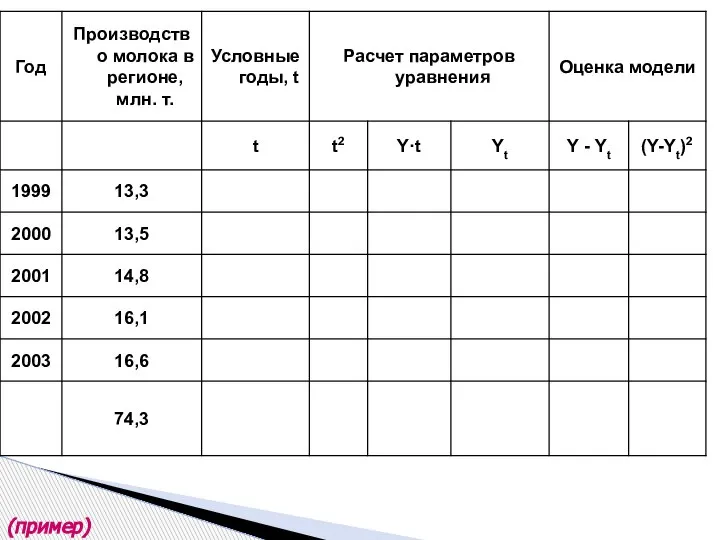
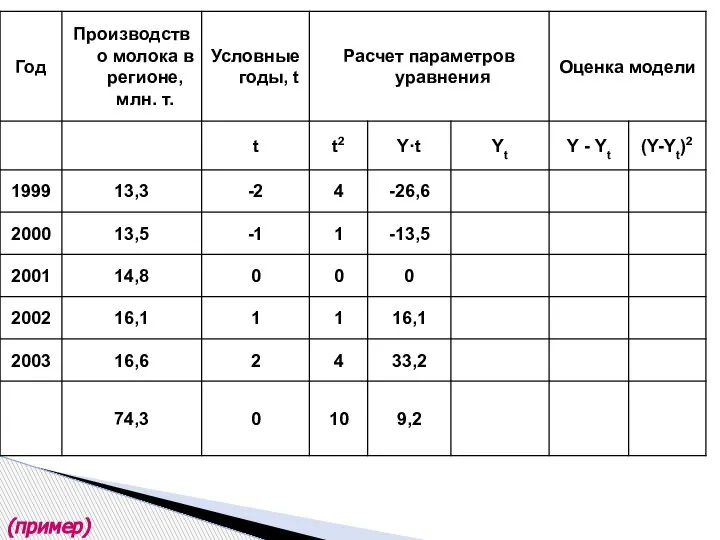
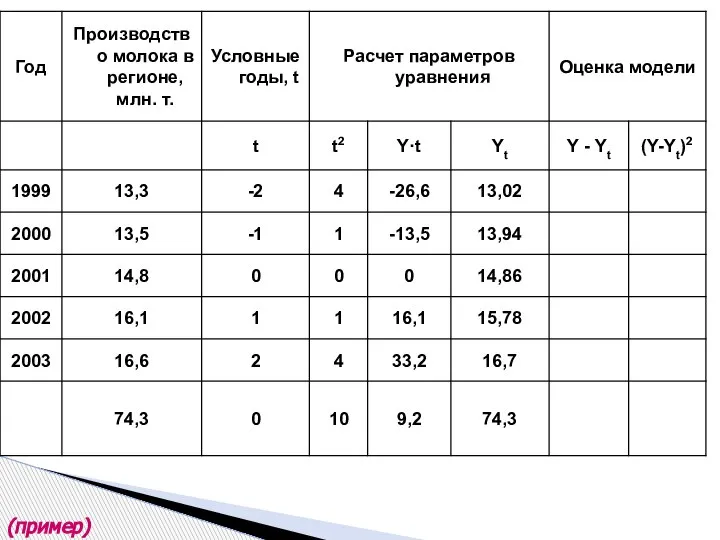
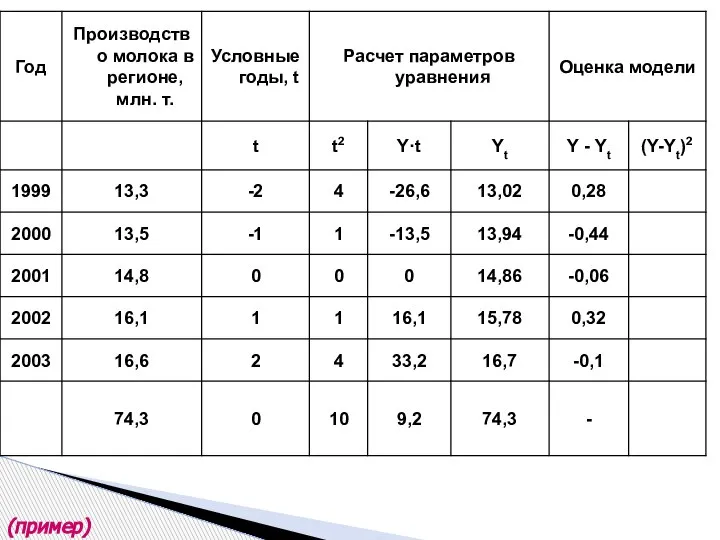
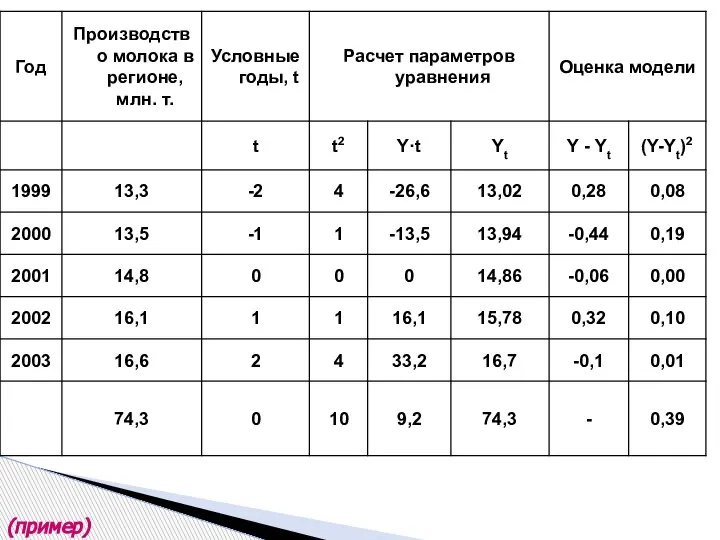
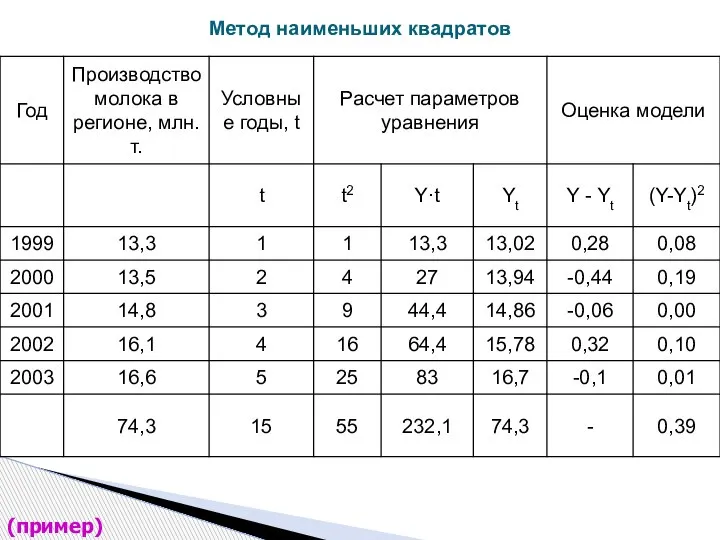
- 35. (пример)
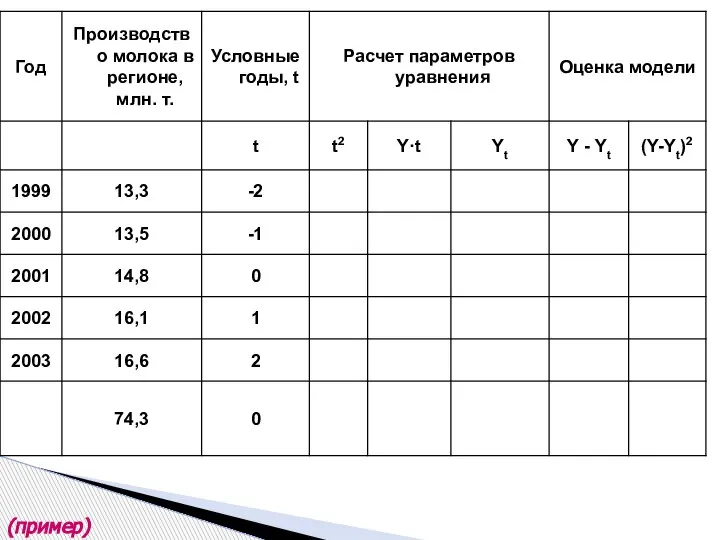
- 36. (пример)
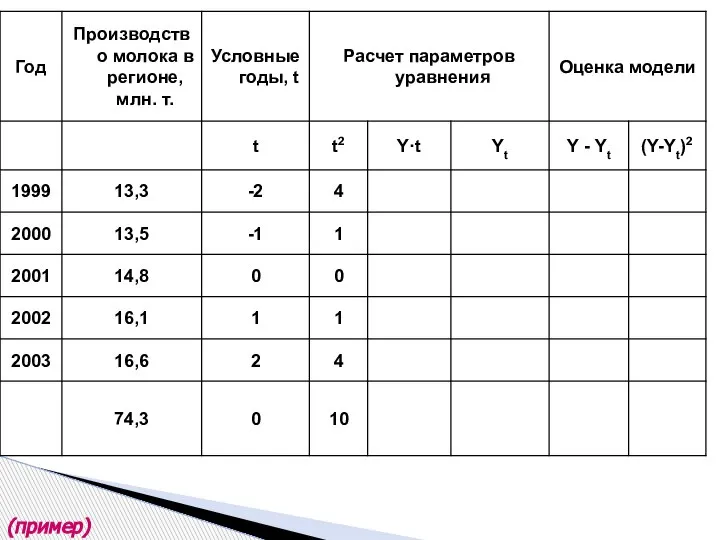
- 37. (пример)
- 38. (пример)
- 39. (пример)
- 40. (пример)
- 41. (пример)
- 43. Для определения колеблемости рассчитывается показатель среднего квадратического отклонения: Относительной мерой колеблемости является коэффициент вариации:
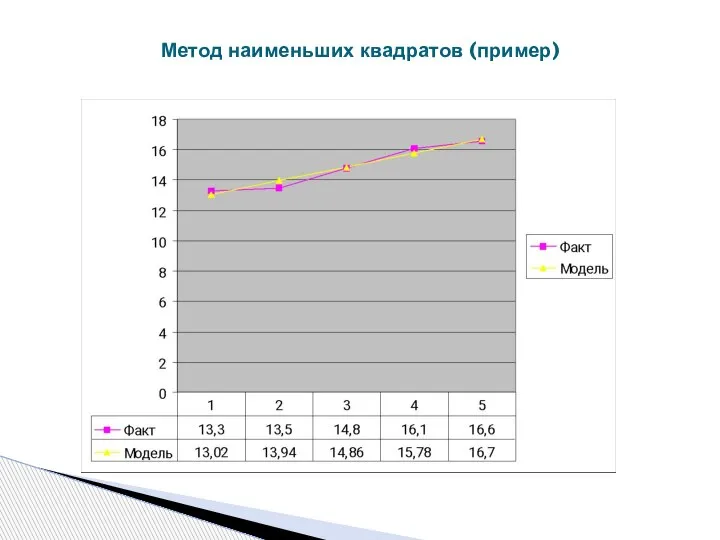
- 44. Метод наименьших квадратов (пример)
- 45. Метод наименьших квадратов (пример)
- 46. Метод наименьших квадратов (пример)
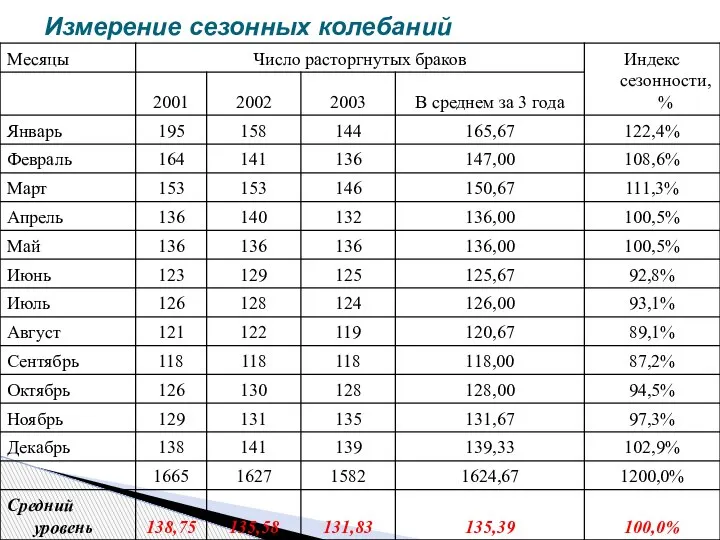
- 47. Измерение сезонных колебаний
- 49. Скачать презентацию




















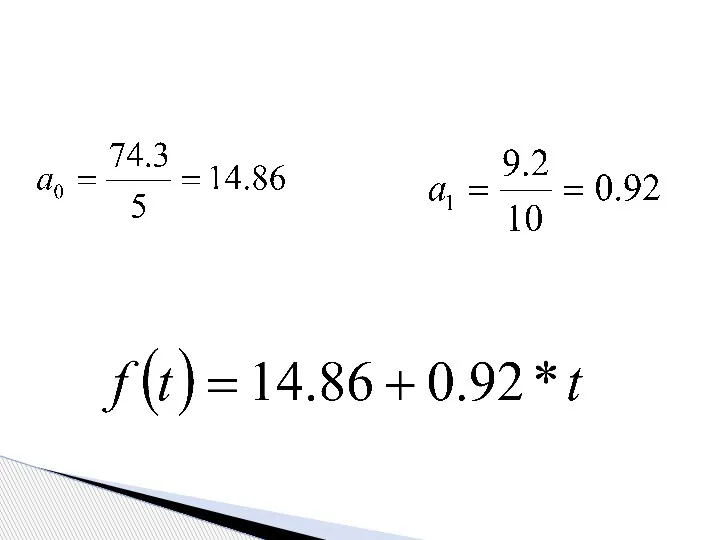


 Особенности истории России. Место России в мировом историческом процессе
Особенности истории России. Место России в мировом историческом процессе Оппортунистические инфекции
Оппортунистические инфекции  Всемирный день борьбы со СПИДом
Всемирный день борьбы со СПИДом Доказательная медицина и стандарты медицинской деятельности
Доказательная медицина и стандарты медицинской деятельности Система счетов и двойная запись
Система счетов и двойная запись Презентация на тему Лепка из пластилина
Презентация на тему Лепка из пластилина  Ночевала тучка золотая
Ночевала тучка золотая Revision
Revision Материально-производственная деятельность человека.
Материально-производственная деятельность человека. Как помочь ребёнку быть внимательным.
Как помочь ребёнку быть внимательным. Защитники земли русской. Работы учеников
Защитники земли русской. Работы учеников Презентация на тему ПОЛИТИЧЕСКИЙ ПРОГНОЗ: сущность, научные основы и принципы
Презентация на тему ПОЛИТИЧЕСКИЙ ПРОГНОЗ: сущность, научные основы и принципы  Словообразование (6 класс)
Словообразование (6 класс) 1 сентября. Классный час «От пера до компьютера».
1 сентября. Классный час «От пера до компьютера». Грамматические особенности перевода арабских фильмов на русский язык
Грамматические особенности перевода арабских фильмов на русский язык 1.3.2 Логические элементы ЭВМ
1.3.2 Логические элементы ЭВМ HTML
HTML Психологический климат в трудовом коллективе
Психологический климат в трудовом коллективе НОУ СОШ Гармония
НОУ СОШ Гармония Китайско-конфуцианская цивилизация
Китайско-конфуцианская цивилизация Каракули. Упражнение 2
Каракули. Упражнение 2 Презентация на тему Треугольники 7 класс геометрия
Презентация на тему Треугольники 7 класс геометрия  Moral Crisis in south Africa
Moral Crisis in south Africa Промоагентство
Промоагентство Презентация на тему Проблема темперамента и характера
Презентация на тему Проблема темперамента и характера Мой творческий путь в прозе и стихах
Мой творческий путь в прозе и стихах ПРОГРАММА«ТРИ ШАГА К УНИКАЛЬНОМУ СЕРВИСУ»GLOBAL SOLUTIONS Ltd.
ПРОГРАММА«ТРИ ШАГА К УНИКАЛЬНОМУ СЕРВИСУ»GLOBAL SOLUTIONS Ltd. Политические режимы. Типы политических режимов
Политические режимы. Типы политических режимов