(у). Но можно составить только одно уравнение: 3х – 5у = 19.
Итак, надо найти значения х и у в данном уравнении. Знаем при этом, что х и у –числа целые и положительные. Уединим то неизвестное, коэффициент которого меньше, т. е. член 3х; получим: 3х = 19 +5у,
откуда х = 19 + = 6 + у + 1+
Так как х, 6 и у – числа целые, то равенство может быть верно лишь при условии,
что 1+ есть также целое число. Обозначим его буквой t.
х=6 + у + t,
Где t = (1+2у)/3
3t=1+2у , 2у=3t-1 => y=(3t-1)/2=t + (t-1)/2
Так как у и t – числа целые, то и (t-1)/2 должно быть некоторым целым числом t1. следовательно,
у = t + t1
t1 = (t - 1)/2
2t1=t - 1 и t= 2t1 +1
Значение t= 2t1 +1 подставляем в предыдущие равенства:
у = t + t1 = (2t1 +1) + t1 = 3t1 + 1,
х = 6 + у + t = 6 + (3t1 + 1) + (2t1 +1) = 8 + 5t1.
Решение.









 Урок математикив 4 классе МБОУ СОШ № 8 г. Туапсе
Урок математикив 4 классе МБОУ СОШ № 8 г. Туапсе Introduction
Introduction TUV NORD CERT GmbH
TUV NORD CERT GmbH Стратегический менеджмент
Стратегический менеджмент Единый государственный экзамен: итоги и перспективы 2010-2011
Единый государственный экзамен: итоги и перспективы 2010-2011 Слава русского оружия
Слава русского оружия Абсолютная гармония !
Абсолютная гармония ! ИЗО
ИЗО Блок-схема от нашей группы на тему: Порядок образования сельскохозяйственного кооператива
Блок-схема от нашей группы на тему: Порядок образования сельскохозяйственного кооператива Методика обучения иностранным языкам
Методика обучения иностранным языкам Технология изготовления изделий из текстильных и нетканых материалов ручным способом
Технология изготовления изделий из текстильных и нетканых материалов ручным способом chto_izuchaet_kurs_obzh
chto_izuchaet_kurs_obzh ЕГЭ по Обществознанию
ЕГЭ по Обществознанию Основные понятия научной дисциплины
Основные понятия научной дисциплины Проектирование учебного процесса по физике на основе педтехнологии В.М. Монахова
Проектирование учебного процесса по физике на основе педтехнологии В.М. Монахова Строение пылевых комплексов, связанных со спутниками планет Орлов С.А. Научно-исследовательский астрономический институт им. В. В.
Строение пылевых комплексов, связанных со спутниками планет Орлов С.А. Научно-исследовательский астрономический институт им. В. В.  Формирование, ведение и использование федерального и регионального учета пуль, гильз и патронов со следами нарезного ручного
Формирование, ведение и использование федерального и регионального учета пуль, гильз и патронов со следами нарезного ручного «у семи нянек дитя без глазу…»или кто должен лечить больного сахарным диабетом 2 типа
«у семи нянек дитя без глазу…»или кто должен лечить больного сахарным диабетом 2 типа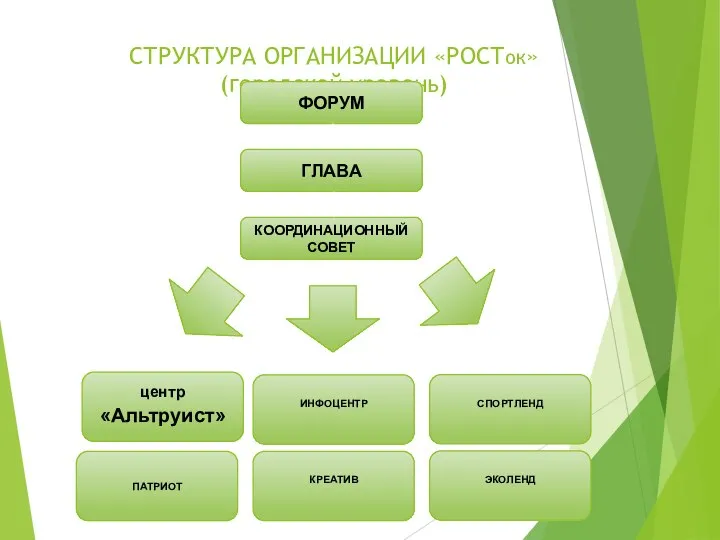 Структура организации РОСТок
Структура организации РОСТок Описание областей влияния базисных вейвлет-функций при помощи ИТ и построение решения задачи Дирихле для некоторых специальных о
Описание областей влияния базисных вейвлет-функций при помощи ИТ и построение решения задачи Дирихле для некоторых специальных о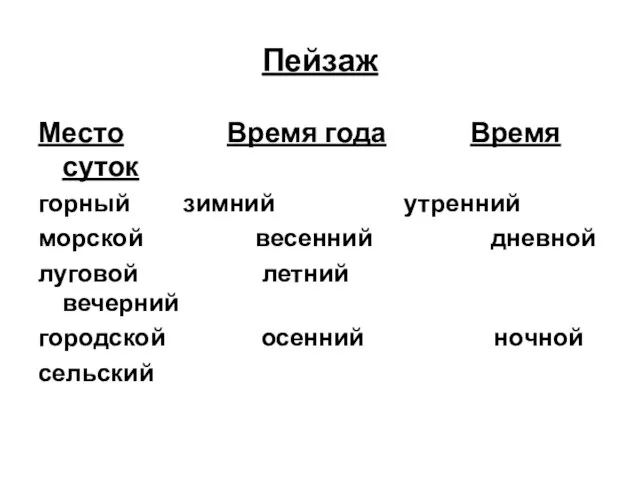 Пейзаж и его разновидности
Пейзаж и его разновидности Основы параллельного программирования с использованием MPI Лекция 1
Основы параллельного программирования с использованием MPI Лекция 1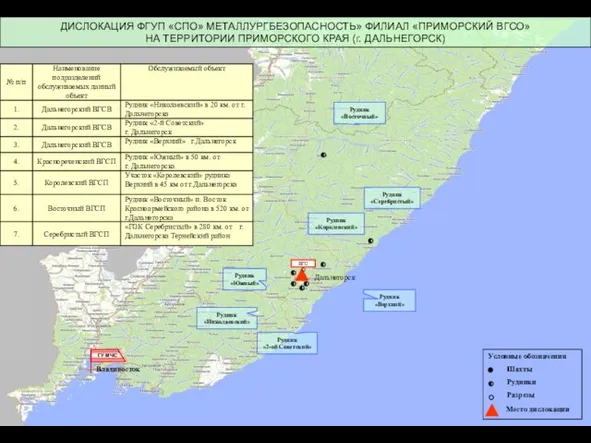 ДИСЛОКАЦИЯ ФГУП «СПО» МЕТАЛЛУРГБЕЗОПАСНОСТЬ» ФИЛИАЛ «ПРИМОРСКИЙ ВГСО» НА ТЕРРИТОРИИ ПРИМОРСКОГО КРАЯ (г. ДАЛЬНЕГОРСК)
ДИСЛОКАЦИЯ ФГУП «СПО» МЕТАЛЛУРГБЕЗОПАСНОСТЬ» ФИЛИАЛ «ПРИМОРСКИЙ ВГСО» НА ТЕРРИТОРИИ ПРИМОРСКОГО КРАЯ (г. ДАЛЬНЕГОРСК) Презентация объекта. Красная поляна
Презентация объекта. Красная поляна Презентация на тему Различие на письме частиц НЕ и НИ
Презентация на тему Различие на письме частиц НЕ и НИ Памятник Петру Великому "Медный всадник"
Памятник Петру Великому "Медный всадник" http://vkontakte.ru/club13752538
http://vkontakte.ru/club13752538 Картина М.В. Нестерова
Картина М.В. Нестерова