Дискретные модели данных в компьютере. Представление чисел

ОБРАЗ КОМПЬЮТЕРНОЙ ПАМЯТИ

ГЛАВНЫЕ ПРАВИЛА ПРЕДСТАВЛЕНИЯ ДАННЫХ В КОМПЬЮТЕРЕ
Правило № 1
Данные (и программы) в памяти компьютера хранятся в двоичном виде, т.е. в виде цепочек единиц и нулей.

Правило № 2
Представление данных в компьютер дискретно.
Дискретизация — преобразование непрерывной функции в дискретную.

Дискретность (от лат. discretus — разделённый, прерывистый), прерывность; противопоставляется непрерывности. Например, дискретное изменение какой-либо величины во времени — это изменение, происходящее через определённые промежутки времени (скачками); система целых чисел (в противоположность системе действительных чисел) является дискретной . В физике и химии Д. означает зернистость строения материи, её атомистичность.
ДИСКРЕТНОСТЬ [discretion] — прерывность; напр., изменение экономических показателей во времени всегда имеет прерывный характер, поскольку происходит скачками — от одной даты (года, месяца и т. д.) к другой. Понятие Д. противопоставляется понятию непрерывности.

Правило № 3
Множество представленных в памяти величин ограничено и конечно.

Представление чисел
в ПК

ЦЕЛЫЕ ЧИСЛА В КОМПЬЮТЕРЕ
Правило № 4
В памяти компьютера числа хранятся в двоичной системе счисления.

ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ФОРМАТЕ С ФИКСИРОВАННОЙ ЗАПЯТОЙ
Целые числа в компьютере хранятся в памяти в формате с фиксированной запятой. В этом случае каждому разряду ячейки памяти соответствует всегда один и тот же разряд числа, а запятая находится справа после младшего разряда, т.е. вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится одна ячейка памяти (8 бит). Например, число A2 = 101010102 будет хранится в ячейке памяти следующим образом:
Максимальное значение целого неотрицательного числа достигается в случае, когда во всех ячейках хранятся единицы. Для n-разрядного представления оно будет равно:
2n - 1

ПРИМЕР. ОПРЕДЕЛИТЬ ДИАПАЗОН ЧИСЕЛ, КОТОРЫЕ МОГУТ ХРАНИТСЯ В ОПЕРАТИВНОЙ ПАМЯТИ В ФОРМАТЕ ЦЕЛОЕ НЕОТРИЦАТЕЛЬНОЕ ЧИСЛО.
Минимальное число соответствует восьми нулям, хранящимся в восьми ячейках памяти, и равно нулю.
Максимальное число соответствует восьми единицам, хранящимся в ячейках памяти и равно:
A = 1*27 +1*26 +1*25 + 1*24 + 1*23 + 1*22 + 1*21 + 1*20 = 1*28 – 1 = 25510
Диапазон изменения целых неотрицательных чисел от 0 до 255.

Для хранения целых чисел со знаком отводится две ячейки памяти (16 бит), причем старший (левый) разряд отводится под знак числа (если число положительное, то в знаковый разряд записывается 0, если число отрицательное записывается 1).
Представление в компьютере положительных чисел с использованием формата «знак-величина» называется прямым кодом числа.

Например, число 200210 = 111110100102 будет представлено в 16-ти разрядном представлении следующим образом:
При представлении целых чисел в n-разрядном представлении со знаком максимальное положительное число (с учетом выделения одного разряда на знак) равно:
A = 2n-1 - 1

ПРИМЕР. ОПРЕДЕЛИТЬ МАКСИМАЛЬНОЕ ПОЛОЖИТЕЛЬНОЕ ЧИСЛО, КОТОРОЕ МОЖЕТ ХРАНИТСЯ В ОПЕРАТИВНОЙ ПАМЯТИ В ФОРМАТЕ ЦЕЛОЕ ЧИСЛО СО ЗНАКОМ.
A10 = 215 – 1 = 3276710
Для представления отрицательных чисел используется дополнительный код. Дополнительный код позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие.
Дополнительный код отрицательного числа A, хранящегося в n ячейках, равен 2n - |A|.

Дополнительный код представляет собой дополнение модуля отрицательного числа А до 0, поэтому в n-разрядной компьютерной арифметике:
2n - |A| + |A| ≡ 0
Это равенство тождественно справедливо, т.к. в компьютерной n-разрядной арифметике
2n ≡ 0. Действительно, двоичная запись такого числа состоит из одной единицы и n нулей, а в n-разрядную ячейку может уместиться только n младших разрядов, т.е. n нулей.

ПРИМЕР. ЗАПИСАТЬ ДОПОЛНИТЕЛЬНЫЙ КОД ОТРИЦАТЕЛЬНОГО ЧИСЛА –2002 ДЛЯ 16-ТИ РАЗРЯДНОГО КОМПЬЮТЕРНОГО ПРЕДСТАВЛЕНИЯ
Проведем вычисления в соответствии с определением дополнительного кода:
Проведем проверку с использованием десятичной системы счисления. Дополнительный код 6353410 в сумме с модулем отрицательного числа 200210 равен 6553610, т.е. дополнительный код дополняет модуль отрицательного числа до 216 (до нуля 16-ти разрядной компьютерной арифметики).
Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:

ПРАВИЛО ПОЛУЧЕНИЯ ДОПОЛНИТЕЛЬНОГО КОДА
Для получения дополнительного кода отрицательного числа можно использовать довольно простой алгоритм:
1. Модуль числа записать прямым кодом в n двоичных разрядах;
2. Получить обратный код числа, для этого значения всех бит инвертировать (все единицы заменить на нули и все нули заменить на единицы);
3. К полученному обратному коду прибавить единицу.

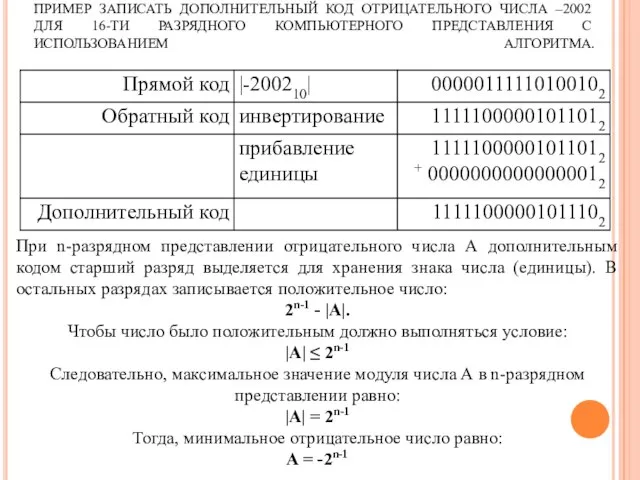
ПРИМЕР ЗАПИСАТЬ ДОПОЛНИТЕЛЬНЫЙ КОД ОТРИЦАТЕЛЬНОГО ЧИСЛА –2002 ДЛЯ 16-ТИ РАЗРЯДНОГО КОМПЬЮТЕРНОГО ПРЕДСТАВЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА.
При n-разрядном представлении отрицательного числа А дополнительным кодом старший разряд выделяется для хранения знака числа (единицы). В остальных разрядах записывается положительное число:
2n-1 - |A|.
Чтобы число было положительным должно выполняться условие:
|A| ≤ 2n-1
Следовательно, максимальное значение модуля числа А в n-разрядном представлении равно:
|A| = 2n-1
Тогда, минимальное отрицательное число равно:
A = -2n-1

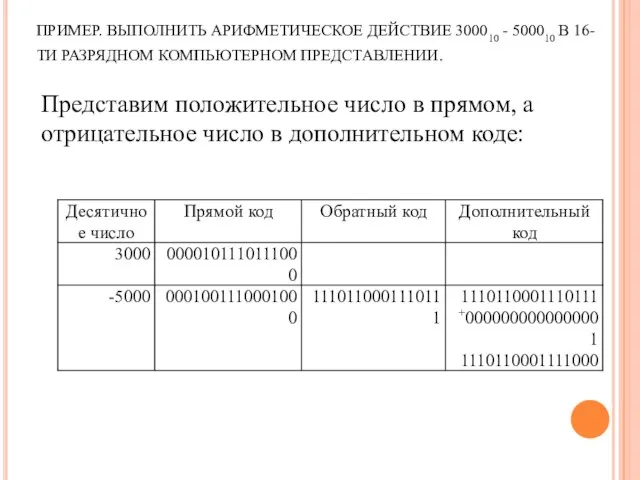
ПРИМЕР. ВЫПОЛНИТЬ АРИФМЕТИЧЕСКОЕ ДЕЙСТВИЕ 300010 - 500010 В 16-ТИ РАЗРЯДНОМ КОМПЬЮТЕРНОМ ПРЕДСТАВЛЕНИИ.
Представим положительное число в прямом, а отрицательное число в дополнительном коде:

СЛОЖИМ ПРЯМОЙ КОД ПОЛОЖИТЕЛЬНОГО ЧИСЛА С ДОПОЛНИТЕЛЬНЫМ КОДОМ ОТРИЦАТЕЛЬНОГО ЧИСЛА. ПОЛУЧИМ РЕЗУЛЬТАТ В ДОПОЛНИТЕЛЬНОМ КОДЕ:
Переведем полученный дополнительный код в десятичное число:
1) Инвертируем дополнительный код: 0000011111001111
2) Прибавим к полученному коду 1 и получим модуль отрицательного числа:
0000011111001111
+ 0000000000000001
0000011111010000

3) Переведем в десятичное число и припишем знак отрицательного числа:
-2000.
Недостатком представления чисел в формате с фиксированной запятой является конечный диапазон представления величин, недостаточный для решения математических, физических, экономических и других задач, в которых используются как очень малые, так и очень большие числа.

Вывод:
Целые числа в памяти компьютера – это дискретное, ограниченное и конечное множество.
Границы множества целых чисел зависят от размера выделяемой ячейки памяти под целое число, а также от формата: со знаком или без знака.

МАТЕМАТИКА:
множество целых чисел дискретно, бесконечно, не ограничено
ИНФОРМАТИКА:
множество целых чисел дискретно, конечно, ограничено