Дискретный анализ

Перестановки
Пусть задано множество из n элементов.
Упорядочение этих элементов называется перестановкой. Иногда добавляют «из n элементов».
Обычно выделяется одно, основное или естественное, упорядочение, которое называется тривиальной перестановкой.
Сами элементы множества A нас не интересуют. Часто в качестве элементов берут целые числа от 1 до n или от 0 до n-1.
Обозначим множество перестановок из n элементов через Pn , а его мощность через Pn.
Зададим все те же три вопроса: чему равно Pn, как перебрать элементы Pn , как их перенумеровать.

Теорема о числе перестановок
Число перестановок из n элементов равно n! - произведению чисел от 1 до n.
(n! читается n–факториал)
Доказательство. По индукции. Для n=1 формула очевидно верна. Пусть она верна для n-1, докажем, что она верна и для n. Первый элемент упорядочения можно выбрать n способами, а к выбранному первому элементу можно способами приписать остальное. Поэтому верна формула Pn= Pn-1×n. Если Pn-1=(n-1)!, то Pn=n!

Нумерация перестановок
Чтобы нумеровать перестановки, мы отобразим множество Pn взаимнооднозначно в другое множество Tn, на котором ввести нумерацию будет гораздо проще, а затем для любого элемента p∈Pn в качестве его номера возьмем номер его образа в Tn.
Множество Tn– это прямое произведение нескольких числовых отрезков
Tn =(0:(n-1))×(0:(n-2)× … ×{0}.
Т.е. каждый элемент Tn– это набор неотрицательных чисел i1, i2, …, in-1, in, причем ik≤n-k.

Отображение
Возьмем перестановку и выпишем рядом с ней тривиальную перестановку. В качестве первого индекса возьмем место первого элемента (считая от нуля) в тривиальной перестановке. Запишем вместо тривиальной перестановки строку оставшихся символов. В качестве второго индекса возьмем место второго элемента перестановки в этой строке. Повторим процесс до конца. Очевидно, что k–й индекс будет меньше длины k–й строки, а последний индекс будет равен нулю.
Посмотрим этот процесс на примере.

Пример отображения
0 1 2 3 4 5 6 Индекс
c a d f g b e a b c d e f g 2
2 a d f g b e a b d e f g 0
2 0 d f g b e b d e f g 1
2 0 1 f g b e b e f g 2
2 0 1 2 g b e b e g 2
2 0 1 2 2 b e b e 0
2 0 1 2 2 0 e e 0
2 0 1 2 2 0 0
Очевидно, что этот процесс обратим и обратное отображение построит по набору индексов исходную перестановку.

Нумерация множества Tn
Любое прямое произведение упорядоченных множеств можно рассматривать как систему счисления с переменным основанием. Вспомните пример с секундами из первой лекции или рассмотрите какую-либо старую шкалу размеров:
1 ярд = 3 фута,
1 фут = 12 дюймов,
1 дюйм = 12 линий,
1 линия = 6 пунктов.
(2, 0, 4, 2, 3) = 2 ярда 0 футов 4 дюйма 2 линии 3 пункта, сколько же это пунктов?
Нужно сосчитать (это называется схемой Горнера)
(((2 × 3+0) × 12+4) × 12+2) × 6+3

Нумерация множества Tn - 2
Формулу #, находящую номер для набора индексов i1, i2, …, in-1, in, мы предпочтем написать в виде рекуррентных выражений
#(i1, i2, …, in) = a(i1, i2, …, in-1,n-1);
a(i1, i2, …, ik,k) = a(i1, i2, …, ik-1,k-1)(n-k+1)+ ik;
a(пусто,0) = 0;
По этой формуле #(2,0,1,2,2,0,0) = a(2,0,1,2,2,0,6).
Имеем
a(2,1)=2; a(2,0,2) = 2×6+0=12;
a(2,0,1,3)=12×5+1=61; a(2,0,1,2,4) =61×4+2=246;
a(2,0,1,2,2,5) =246×3+2=740;
a(2,0,1,2,2,0,6) =740×2+0=1480;

Перебор наборов индексов
Исходя из вышеизложенного, перебрать перестановки просто: нужно перебрать все наборы индексов из и по каждому набору строить соответствующую ему перестановку.
Для перебора наборов индексов заметим, что фактически каждый набор – это запись числа в особой системе счисления с переменным основанием (система называется факториальной).
Правила прибавления 1 в этой системе почти так же просты, как в двоичной: двигаясь от последнего разряда пытаться прибавить в текущем разряде 1. Если это возможно, то прибавив 1 остановиться. Если невозможно, записать в разряд нуль и перейти к следующему разряду.

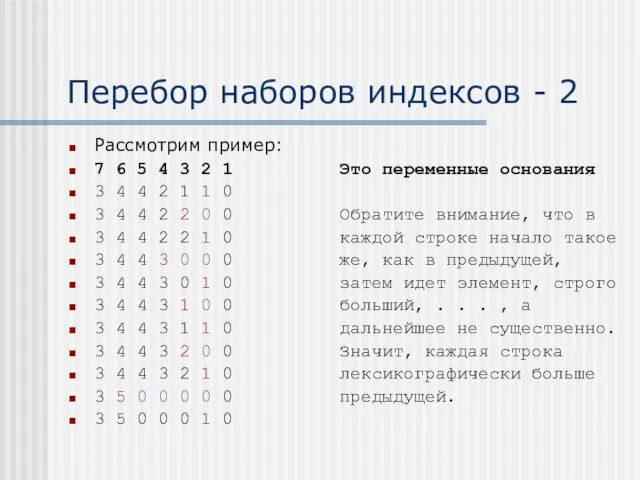
Перебор наборов индексов - 2
Рассмотрим пример:
7 6 5 4 3 2 1 Это переменные основания
3 4 4 2 1 1 0
3 4 4 2 2 0 0 Обратите внимание, что в
3 4 4 2 2 1 0 каждой строке начало такое
3 4 4 3 0 0 0 же, как в предыдущей,
3 4 4 3 0 1 0 затем идет элемент, строго
3 4 4 3 1 0 0 больший, . . . , а
3 4 4 3 1 1 0 дальнейшее не существенно.
3 4 4 3 2 0 0 Значит, каждая строка
3 4 4 3 2 1 0 лексикографически больше
3 5 0 0 0 0 0 предыдущей.
3 5 0 0 0 1 0

Теорема о лексикографическом переборе перестановок
Описанный алгоритм перебирает перестановки в порядке лексикографического возрастания.
Доказательство. Нам достаточно показать, что если мы имеем два набора индексов I1 и I2, и I1 лексикографически предшествует I2, то перестановка π(I1) лексикографически предшествует π(I2).
Эти перестановки формируются последовательно, и пока совпадают I1 и I2, совпадают и их перестановки. А большему значению индекса соответствует и больший элемент.

Прямой алгоритм лексикографического перебора перестановок
Возьмем какую-либо перестановку p и прямо найдем лексикографически следующую.
Возьмем начало – первые k элементов. Среди его продолжений известны минимальное, в котором все элементы расположены по возрастанию, и максимальное, в котором по убыванию.
Например, в перестановке p =(4, 2, 1, 7, 3, 6, 5) все продолжения для (4, 2, 1) лежат между (3, 5, 6, 7) и (7, 6, 5, 3). Имеющееся продолжение меньше максимального, и 3-й элемент еще можно не менять. И 4-й тоже. А 5-й нужно сменить. Для этого из оставшихся элементов нужно взять следующий по порядку, поставить его 5-м и приписать минимальное продолжение. Получится (4, 2, 1, 7, 5, 3, 6).

Прямой алгоритм лексикографического перебора перестановок - 2
Выпишем несколько следующих перестановок.
(4, 2, 1, 7, 5, 3, 6)
(4, 2, 1, 7, 5, 6, 3)
(4, 2, 1, 7, 6, 5, 3)
(4, 2, 3, 1, 5, 6, 7)
(4, 2, 3, 1, 5, 7, 6)
(4, 2, 3, 1, 6, 5, 7)
(4, 2, 3, 1, 6, 7, 5)
(4, 2, 3, 1, 7, 5, 6)
(4, 2, 3, 1, 7, 6, 5)
(4, 2, 3, 5, 1, 6, 7)

Формальное описание алгоритма
Рабочее состояние: Перестановка p и булев признак isActive.
Начальное состояние: В записана тривиальная перестановка и isActive = True.
Стандартный шаг:
Если isActive, выдать перестановку в качестве результата.
Двигаясь с конца, найти в перестановке наибольший монотонно убывающий суффикс. Пусть k – позиция перед суффиксом.
Положить isActive := (k > 0).
Если isActive, то найти в суффиксе наименьший элемент, превосходящий pk, поменять его местами с pk, а потом суффикс «перевернуть».

Еще алгоритм перебора перестановок
Попробуем теперь перебрать перестановки так, чтобы две последовательные перестановки мало отличались друг от друга. Насколько мало? На одну элементарную транспозицию, в которой меняются местами два соседних элемента.
Возможно ли это? Покажем принципиальную схему такого алгоритма, нам будет интересна именно она.
Представьте себе n-1 элементарных «механизмов», каждый из передвигает свой элемент внутри набора. На каждом шаге механизм делает сдвиг налево или направо. Направление меняется, когда элемент доходит до края. На смену направления тратится один шаг, во время которого шаг делает следующий механизм, который, впрочем, тоже может менять направление.

Еще алгоритм перебора перестановок -2
Посмотрим пример.
1 2 3 4 5 Чей ход 1 2 3 4 5 Чей ход
a b c d e a c d a b e a
b a c d e a c d b a e a
b c a d e a c d b e a b
b c d a e a c d e b a a
b c d e a b c d e a b a
c b d e a a c d a e b a
c b d a e a c a d e b a
c b a d e a a c d e b c
c a b d e a a d c e b a
a c b d e b d a c e b a
a c d b e a d c a e b a
c a d b e a d c e a b a

Перебор перестановок. 1
function ExistsNextPerm(var kCh: integer): Boolean;
var iV,iP,iVC,iPC: integer;
begin
result := False;
for iV := nV downto 2 do
if count[iV] < iV-1 then begin
Inc(count[iV]); iP := pos[iV];
iPC := iP+dir[iV]; iVC := perm[iPC];
perm[iP] := iVC; perm[iPC] := iV;
pos[iVC] := iP; pos[iV] := iPC;
kCh := iP; if dir[iV] < 0 then Dec(kCh);
result := True; exit;
end else begin
count[iV] := 0; dir[iV] := - dir[iV];
end;
end;

Задача о минимуме суммы попарных произведений
Пусть заданы два набора по n чисел, скажем, {ak|k∈1:n} и {bk|k∈1:n} . Эти числа разбиваются на пары (ak,bk) и вычисляется сумма их попарных произведений ∑k∈1:n akbk. Можно менять нумерацию {ak} и {bk}.
Требуется выбрать такую нумерацию, при которой сумма минимальна.
В этой задаче можно зафиксировать какие-то нумерации {ak} и {bk} и искать перестановку π, для которой достигается минимум суммы ∑k∈1:n akbπ(k).
Мы выберем нумерации, когда {ak} расположены по возрастанию, а {bk} – по убыванию.

Теорема о минимуме суммы попарных произведений
Минимум суммы попарных произведений достигается на тривиальной перестановке.
Доказательство. Предположим, что существуют такие два индекса k и r, что ak < ar и bk < br . В этом случае
(ar−ak)(br −bk) > 0, т.е. ar br + ak bk > ar bk + ak br .
В нашей нумерации {ak} расположены по возрастанию. Если {bk} расположены не по возрастанию, то найдется такая пара k и r, как сказано выше. Переставив у этой пары bk и br , мы уменьшим значение суммы. Значит, в оптимальном решении {bk} стоят по возрастанию.
Эта простая теорема несколько раз встретится нам в дальнейшем.

Задача о максимальной возрастающей подпоследовательности
Задана последовательность {ak|k∈1:n} чисел длины n. Требуется найти ее последовательность наибольшей длины, в которой числа {ak} шли бы в возрастающем порядке.
Например, в последовательности
3, 2, 11, 14, 32, 16, 6, 17, 25, 13, 37, 19, 41, 12, 7, 9
максимальной будет подпоследовательность
2, 11, 14, 16, 17, 25, 37, 41
С перестановками эта задача связана тем, что исходная последовательность может быть перестановкой.
Мы ограничимся тем, что покажем, как решается эта задача, а формализацию и обоснование алгоритма предоставим слушателям.

Нахождение максимальной возрастающей подпоследовательности
Будем по возможности экономно разбивать нашу на убывающие последовательности (пример изменен)
9 12 11 14 18 16 6 17 15 13 37 19 21 8 7 5
9 6 5
12 11 8 7
14 13
18 16 15
17
37 19
21
Каждое следующее число пишется в самую верхнюю из строчек, где оно не нарушит порядка. Возьмем число из нижней строчки, 21. Почему оно стоит в 8-й строчке? Ему мешает 19. А числу 19 мешает 17. А ему 16. И т. д.
Последовательность 9, 11, 14, 16, 17, 19, 21 возрастает и имеет длину 7. Любая последовательность большей длины содержит два числа из одной строки (принцип Дирихле) и не может быть возрастающей.

Задача о минимальном числе инверсий
Задана последовательность {ak|k∈1:n} чисел длины n. Инверсией назовем выполняемое на месте зеркальное отражение какой-либо ее подстроки – сплошной подпоследовательности.Требуется за минимальное число инверсий расположить элементы последовательности по возрастанию.
Например, перестановку «сплошная» можно преобразовывать так (красные буквы переставлены, большие уже стоят на месте)
сплошнаЯ
сплоанШЯ
наолПСШЯ
АнолПСШЯ
АнлОПСШЯ
АЛНОПСШЯ (за пять инверсий)

Экзаменационные вопросы
Перестановки. Их перебор и нумерация.
Задача о минимуме скалярного произведения.
Задача о наибольшей возрастающей подпоследовательности.