Добро пожаловать!

Квадратные уравнения.
Учитель математики МБОУ СОШ с. Ачан
Артёмова Ольга Анатольевна

"Предмет математики настолько серьезен, что полезно не упускать случая делать его немного занимательным".
Паскаль

Тест
«Квадратные уравнения»
Показать ответ

1 вариант:
1) квадратным уравнением
2) отрицательный
3) приведенным квадратным уравнением
4) положительное число
5) 1
2 вариант:
1) первый коэффициент, свободный член
2) не имеет корней
3) равно нулю
4) неполным
5) 4
Ответы к тесту:

Угадайте, что в черном ящике?
Определения этому предмету:
Непроизводная основа слова.
Число, которое после
подстановки его в уравнение обращает уравнение в тождество.
Один из основных органов растений.

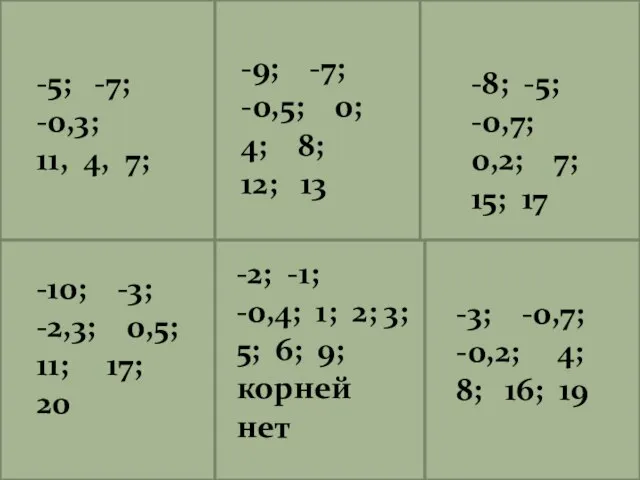
-5; -7; -0,3;
11, 4, 7;
-2; -1;
-0,4; 1; 2; 3; 5; 6; 9; корней нет
-9; -7; -0,5; 0; 4; 8;
12; 13
-8; -5; -0,7; 0,2; 7; 15; 17
-10; -3; -2,3; 0,5; 11; 17; 20
-3; -0,7; -0,2; 4; 8; 16; 19

Проверьте решение!

Древняя Индия
Задачи на квадратные уравнения встречаются уже в 499 г. В Древней Индии были распространены публичные соревнования в решении трудных задач.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Лишь в 17 в. благодаря трудам Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

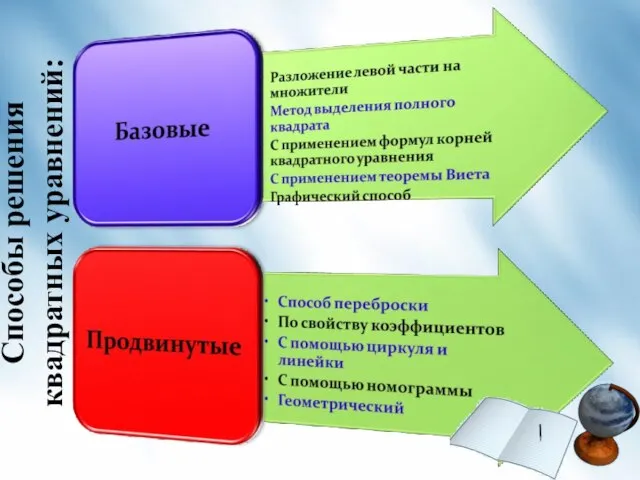
Способы решения
квадратных уравнений:

Решение квадратных уравнений по свойству коэффициентов

Пусть дано квадратное уравнение
ах2 + bх + с = 0, где а ≠0.
Свойство 1.
Если а + b + с = 0 (т е. сумма коэффициентов уравнения равна нулю), то х1 = 1, х2 = с/а
Свойство 2.
Если а – b + с = 0, или b = а + с, то
х1 = – 1, х2 = – с/а

Пример:

Пример:

1 вариант:
2 вариант:
Ответ:

1 вариант:
2 вариант:

Вывод:
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт»
У. Сойер

Домашнее задание:
Формулы для решения квадратного уравнения
№ 654 (1 столбик)