Содержание
- 2. Двумерные многообразия Пусть и – два множества в евклидовом пространстве произвольной размерности. Если задано отображение ,
- 3. Двумерные многообразия Например, поверхность куба гомеоморфна сфере (рис.2) Рис. 2
- 4. Двумерные многообразия Рис. 3
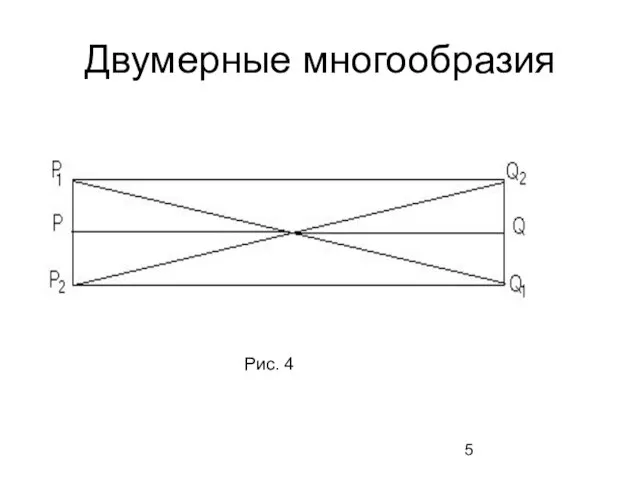
- 5. Двумерные многообразия Рис. 4
- 6. Двумерные многообразия Рис. 5
- 7. Двумерные многообразия Любая компактная двумерная поверхность гомеоморфна либо сфере с p ручками, либо сфере с q
- 8. Двумерные многообразия Рис. 7
- 9. Двумерные многообразия Рис.8
- 10. Двумерные многообразия Рис.9
- 11. Двумерные многообразия Рис. 10
- 12. Фундаментальная группа Рис. 11 Две петли и , проходящие через фиксированную точку P , называются гомотопными,
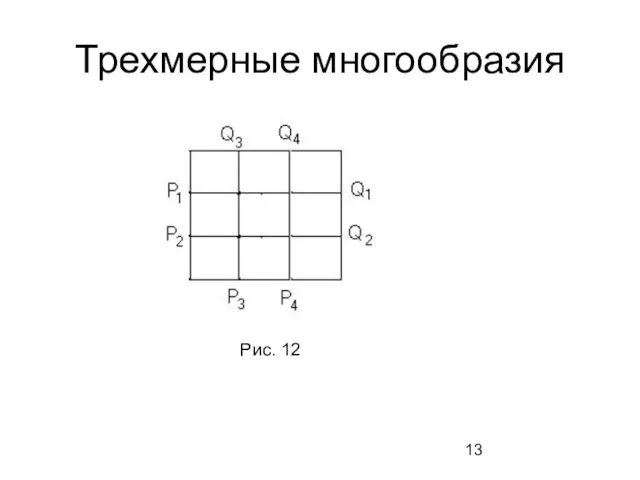
- 13. Трехмерные многообразия Рис. 12
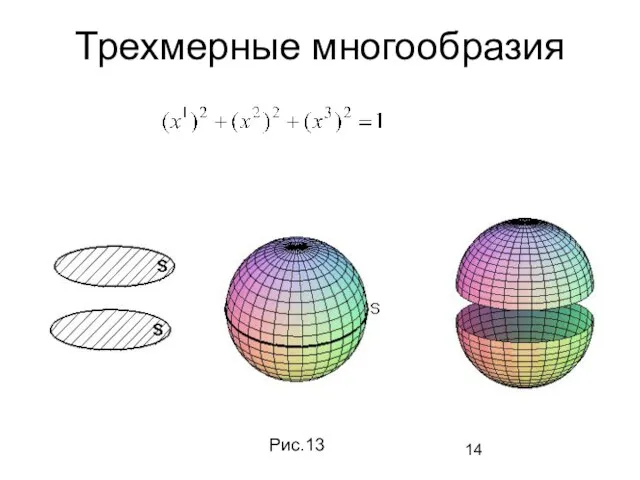
- 14. Трехмерные многообразия Рис.13
- 15. Трехмерные многообразия Каждое компактное ориентируемое 3-мерное многообразие раскладывается в связную сумму где сомножители - замкнутые неприводимые
- 16. Трехмерные многообразия Рис. 14
- 17. Трехмерные многообразия Любое трехмерное компактное неприводимое многообразие можно разрезать конечным числом несжимающихся торов на компактные многообразия,
- 18. А. Пуанкаре в 1904г высказал гипотезу, что любое компактное односвязное трехмерное многообразие гомеоморфно трехмерной сфере .
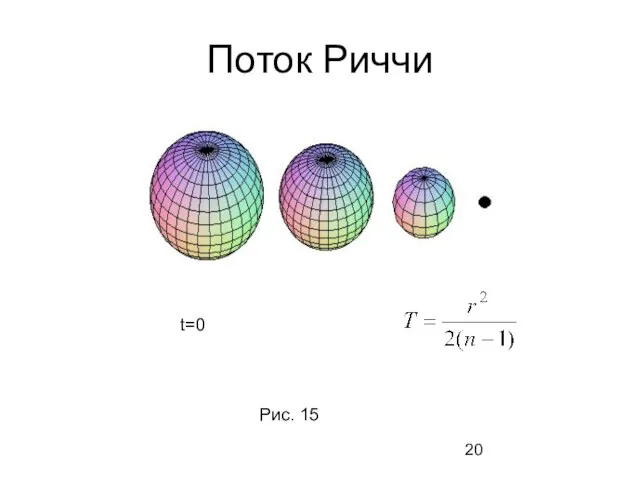
- 19. Поток Риччи Пусть есть риманово неприводимо компактное многообразие, на котором в локальных координатах метрика задается в
- 20. Поток Риччи t=0 Рис. 15
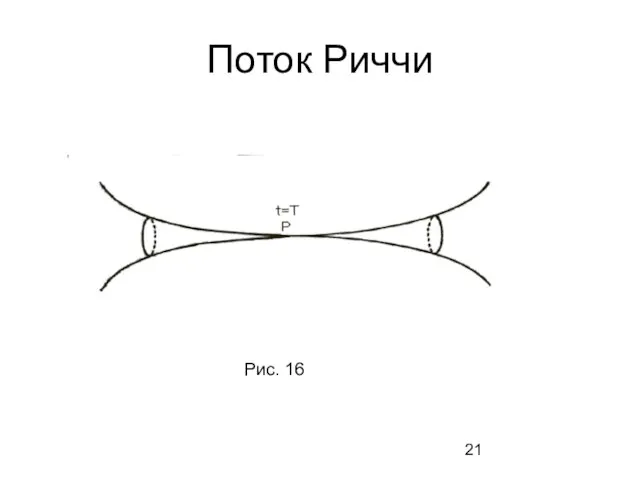
- 21. Поток Риччи Рис. 16
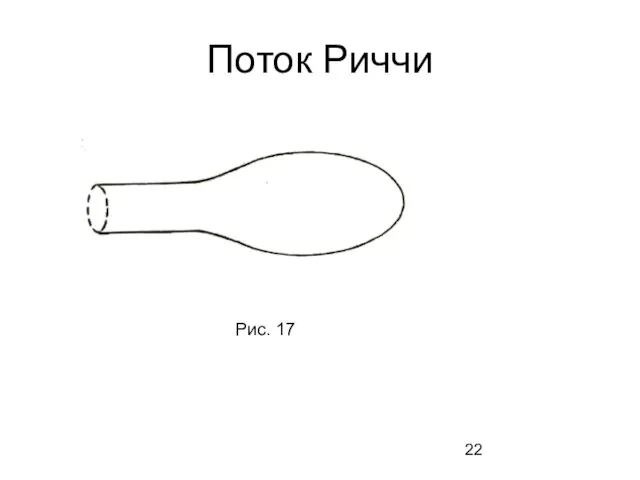
- 22. Поток Риччи Рис. 17
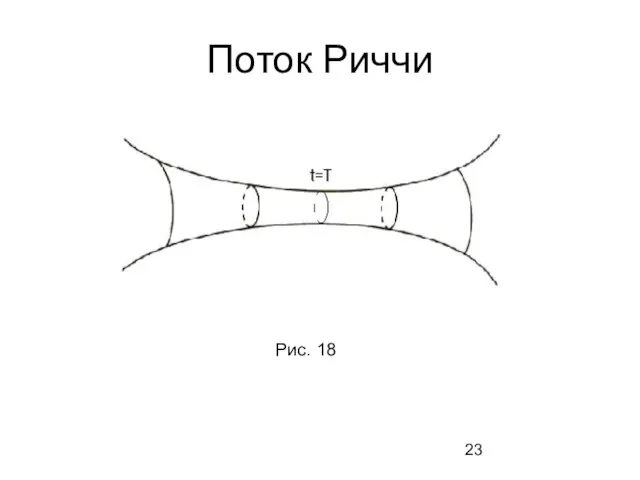
- 23. Поток Риччи Рис. 18
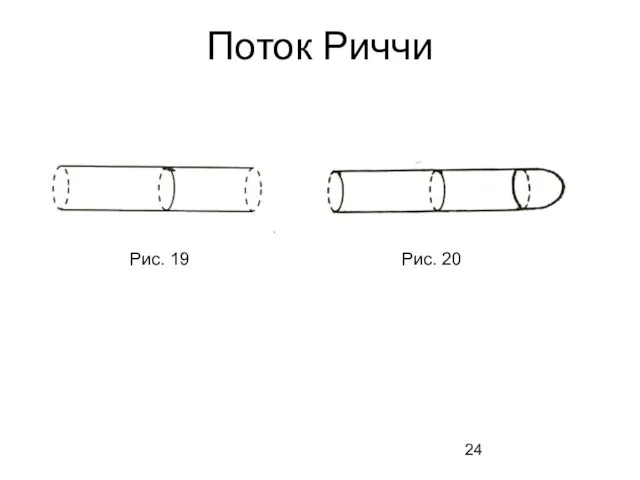
- 24. Поток Риччи Рис. 19 Рис. 20
- 25. Поток Риччи Рис. 21
- 26. Sylvia Nasar and David Cruber. Manifold Destiny. A legendary problem and the battle over who soved
- 27. Принцип максимума и функция Ляпунова А.М. Ляпунов (1857-1918)
- 29. Я хочу показать, как фактически использовалась идея функций Ляпунова в принципе максимума Р.Гамильтона, который являлся существенным
- 30. Определение. Положение равновесия называется устойчивым по Ляпунову, если для любого и существует положительное число такое, что
- 31. Заметим, что при малых положительных множество точек в пространстве является замкнутой гиперповерхностью , гомеоморфной сфере ,
- 32. Так как удовлетворяют системе (2), то (4) , где по идет суммирование от 1 до .
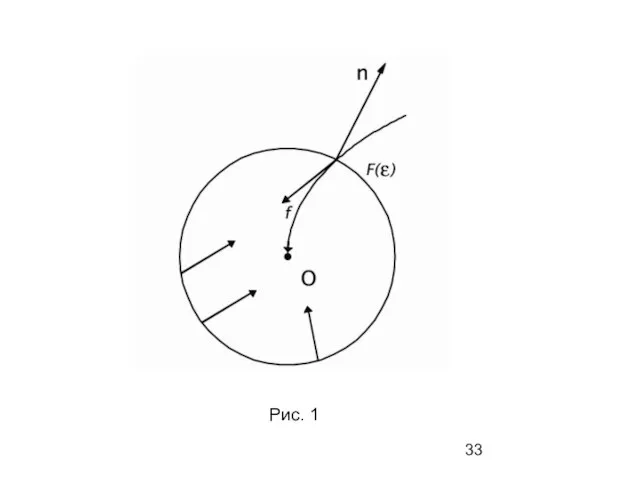
- 33. Рис. 1
- 34. Ясно, что (7) где направлен по нормали гиперповерхности вне компактной области , которую ограничивает гиперповерхность и
- 35. Мы рассматриваем как отображение M в евклидово пространство . Пусть U -открытое множество в и –
- 36. в области и зададим тот же вопрос: когда решение системы (10) останется в X ? Пусть
- 38. Скачать презентацию

























 You can read
You can read Презентация на тему Радиационный фон школьных помещений
Презентация на тему Радиационный фон школьных помещений  Презентация на тему Древние экологические катастрофы – гипотезы и факты
Презентация на тему Древние экологические катастрофы – гипотезы и факты Геометрические паркеты
Геометрические паркеты " Золотой век русской культуры"
" Золотой век русской культуры" Образование и наука России в начале и середине XIX века
Образование и наука России в начале и середине XIX века Сам себе предприниматель: как зарабатывать и экономить на шеринге. Leaders Talk
Сам себе предприниматель: как зарабатывать и экономить на шеринге. Leaders Talk Климат Северной Америки
Климат Северной Америки Происхождение государства и права: органическая теория
Происхождение государства и права: органическая теория Будущее компьютера Ирина Хрулёва
Будущее компьютера Ирина Хрулёва Нормативные модели ППР - функции
Нормативные модели ППР - функции Welcome презентация для контент-менеджеров new
Welcome презентация для контент-менеджеров new Праздник салата
Праздник салата Европа перед мировым пожаром
Европа перед мировым пожаром Презентация на тему Условия прорастания семян
Презентация на тему Условия прорастания семян  Микрофазное расслоение в расплаве двойных гребнеобразных сополимеров
Микрофазное расслоение в расплаве двойных гребнеобразных сополимеров Презентация на тему Одиссея Гомера
Презентация на тему Одиссея Гомера Сравнительная оценка различных методов дворового компостирования
Сравнительная оценка различных методов дворового компостирования Система бухгалтерских счетов и двойная запись
Система бухгалтерских счетов и двойная запись Общественные советы при органах исполнительной власти Брянской области: правовая основа деятельности и реализуемые полномочия
Общественные советы при органах исполнительной власти Брянской области: правовая основа деятельности и реализуемые полномочия МИЦАР – Аналитический блок Автоматизированный программный комплекс по учету работы и движения погружного насосного оборудовани
МИЦАР – Аналитический блок Автоматизированный программный комплекс по учету работы и движения погружного насосного оборудовани Консоли колонн
Консоли колонн Достопримечательности с.Кытманово
Достопримечательности с.Кытманово НАШЕ ЗДОРОВЬЕ-В НАШИХ РУКАХ
НАШЕ ЗДОРОВЬЕ-В НАШИХ РУКАХ Как победить мобильный спам
Как победить мобильный спам My native town Lugansk
My native town Lugansk  ООО Энергосвет
ООО Энергосвет Презентация на тему Линейная функция и её график
Презентация на тему Линейная функция и её график