Микрофазное расслоение в расплаве двойных гребнеобразных сополимеров

Микрофазное расслоение
Диблок-сополимер
1

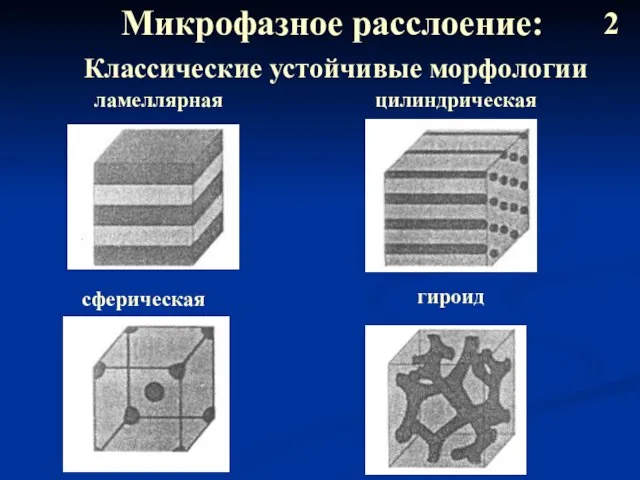
Микрофазное расслоение:
Классические устойчивые морфологии
ламеллярная
цилиндрическая
сферическая
гироид
2

Микрофазное расслоение:
Возможные области применения периодических структур
1. Создание систем с высокой плотностью записи информации
2. Использование структур в качестве шаблонов для упаковки наночастиц
3. Изготовление фотонных кристаллов
3
Park C., Yoon J., Thomas E.L., Enabling nanotechnology with self-assembled block-copolymer patterns. Polymer, 2003, 44, 6725-6760

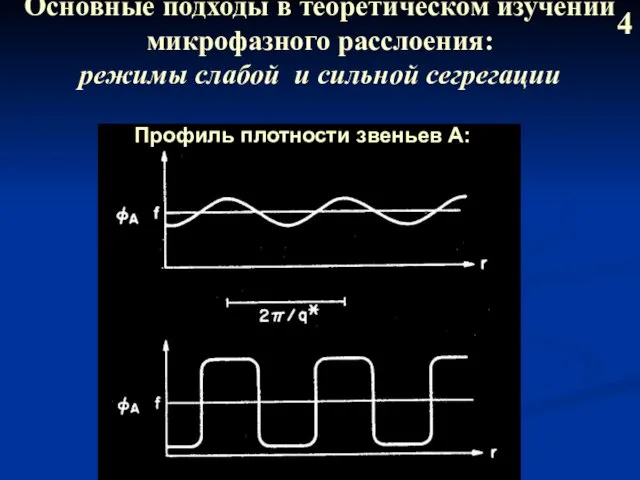
Основные подходы в теоретическом изучении
микрофазного расслоения:
режимы слабой и сильной сегрегации
4
Профиль плотности звеньев A:

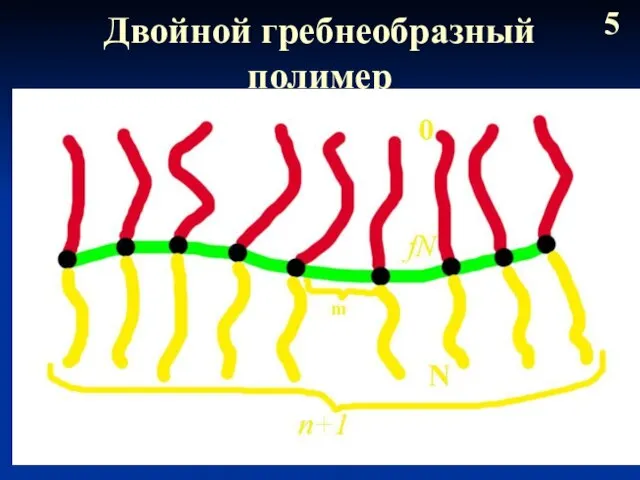
Двойной гребнеобразный полимер
5

Синтез двойных гребнеобразных полимеров
Zhu Y., Weildisch R., Gido S.P., Velis G., Hadjichristidis N., Morphologies and Mechanical Properties of a Series of Block-Double-Graft Copolymers and Terpolymers. Macromolecules, 2002, 35, 5903-5909
6

Основные предположения
при теоретическом анализе задачи
Слабая сегрегация
Одинаковые размеры звеньев
Взаимодействия звеньев описываются параметрами χij
Расчет произведен в ПСФ (квадратичное приближение)
7

1. Плотнопривитой блок-сополимер (m = 1):
1.1 Стереорегулярный случай
1.2 Нестереорегулярный случай
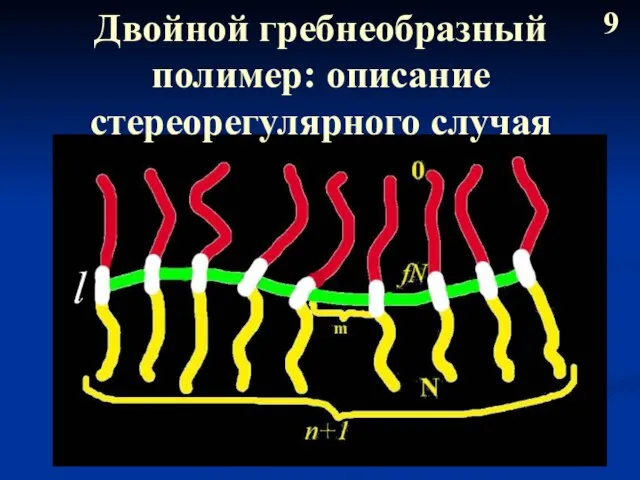
2. Случай m ≠ 1. Рассмотрены все 5 случаев, в которых взаимодействия описываются одним параметром Флори-Хаггинса
8

Двойной гребнеобразный полимер: описание стереорегулярного случая
9

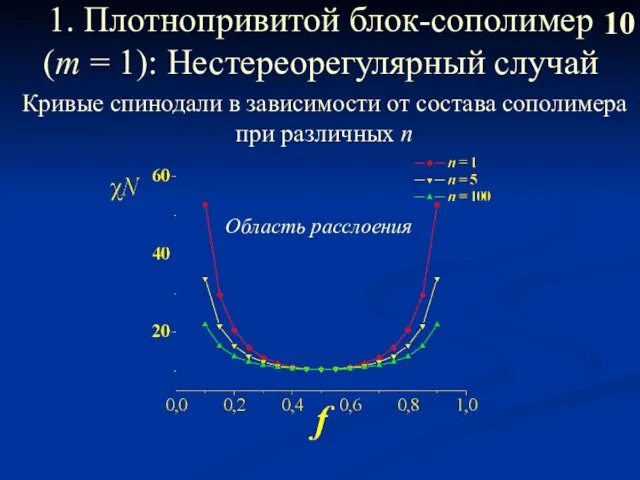
10
1. Плотнопривитой блок-сополимер (m = 1): Нестереорегулярный случай
Кривые спинодали в зависимости от состава сополимера
при различных n
Область расслоения

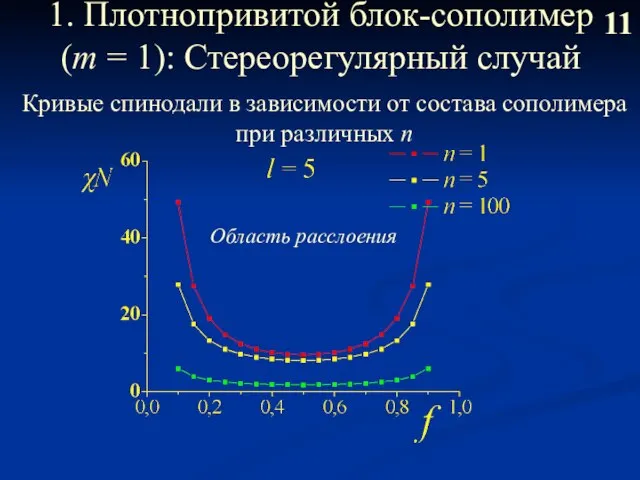
1. Плотнопривитой блок-сополимер (m = 1): Стереорегулярный случай
11
Кривые спинодали в зависимости от состава сополимера
при различных n
Область расслоения

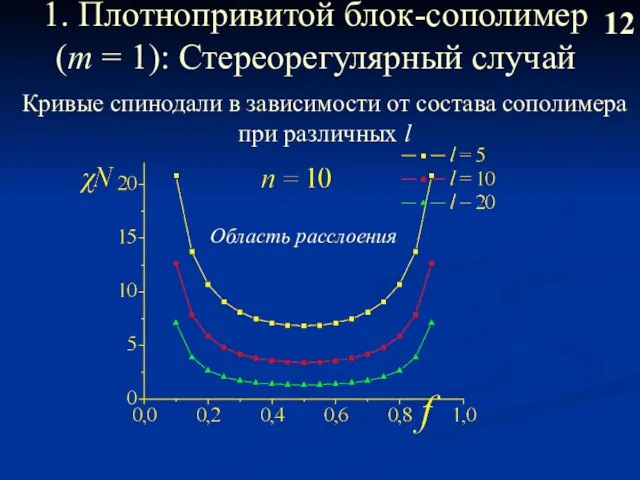
1. Плотнопривитой блок-сополимер (m = 1): Стереорегулярный случай
12
Кривые спинодали в зависимости от состава сополимера
при различных l
Область расслоения

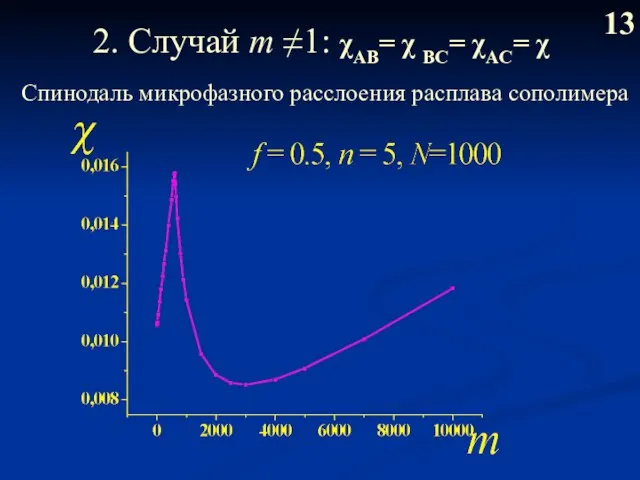
2. Случай m ≠1: χAB= χ BС= χAC= χ
13
Спинодаль микрофазного расслоения расплава сополимера

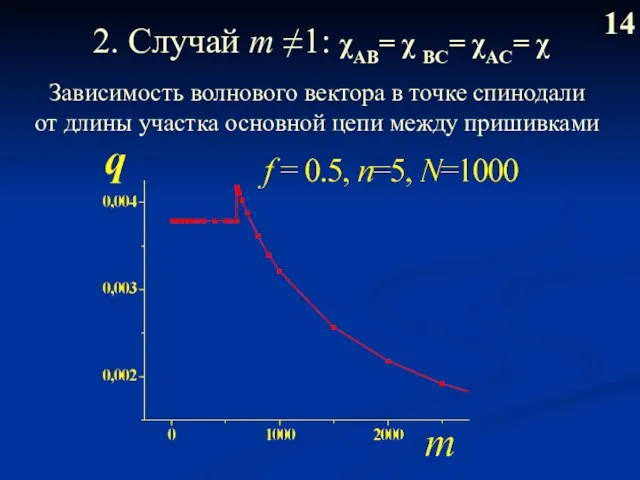
2. Случай m ≠1: χAB= χ BС= χAC= χ
14
Зависимость волнового вектора в точке спинодали
от длины участка основной цепи между пришивками

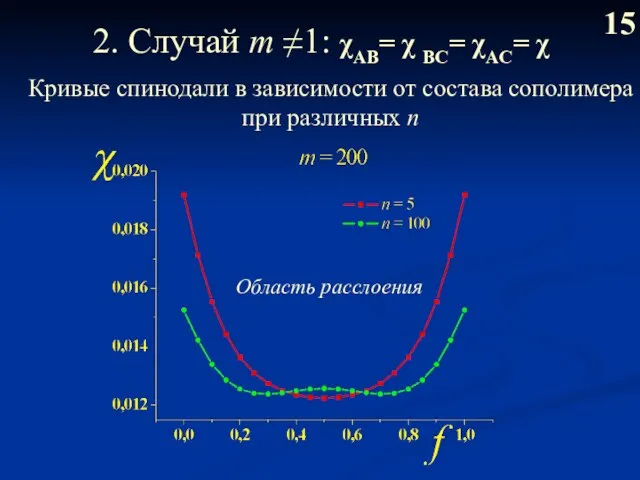
2. Случай m ≠1: χAB= χ BС= χAC= χ
15
Кривые спинодали в зависимости от состава сополимера
при различных n
Область расслоения

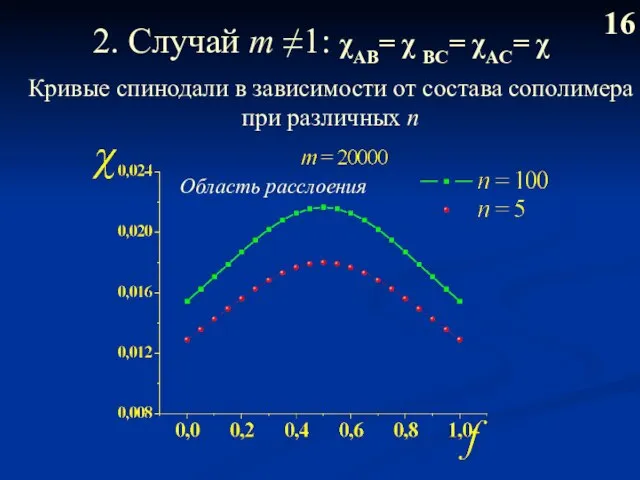
2. Случай m ≠1: χAB= χ BС= χAC= χ
16
Кривые спинодали в зависимости от состава сополимера
при различных n
Область расслоения

Выводы
Исследован переход из однородного состояния в упорядоченное для плотной пришивки боковых цепей.
В случае стереорегулярного расположения цепей поведение системы при росте n меняется по сравнению с нестереорегулярным случаем: вне зависимости от состава при росте n χN в точке перехода уменьшается.
17

Выводы
Исследованы все случаи, в которых взаимодействия описываются одним параметром Флори-Хаггинса при m ≠ 1.
Построены спинодали и зависимости волнового вектора в точке перехода от параметров задачи и проведена интерпретация данных зависимостей.
Обнаружена возможность существования явления двухмасштабной неустойчивости в расплавах двойных гребнеобразных полимеров
18

Аналитические результаты
19