Дотична до графіка функції

Дотична до графіка функції
Мета: Дати поняття про геометричний зміст похідної та вивести рівняння дотичної

І. Перевірка домашнього завдання
1. Розв’язати нерівності методом інтервалів:
2.
2.
1.
1.
2. Знайти похідні функцій:
1.
1.
2.
2.

І. Перевірка домашнього завдання
1. Розв’язати нерівності методом інтервалів:
2.
2.
1.
1.
2. Знайти похідні функцій:
1.
1.
2.
2.
–1 3 5
–6 –2 4
(–∞;–1)U(3;5)
відповіді
[-6;-2]U[4;+∞)
1 3
–2 3 4
(1;3] і х=0
(–∞;-2)U(-2;-3)U(4;+∞)

ІІ. Вивчення нового матеріалу
А) Актуалізація опорних знань.
Що називається похідною функції?
Який геометричний і механічний зміст похідної?
Що таке січна? Який кутовий коефіцієнт січної?
Дати поняття дотичної до графіка функції.
Б) Мотивація навчання.
Коротка історична довідка.

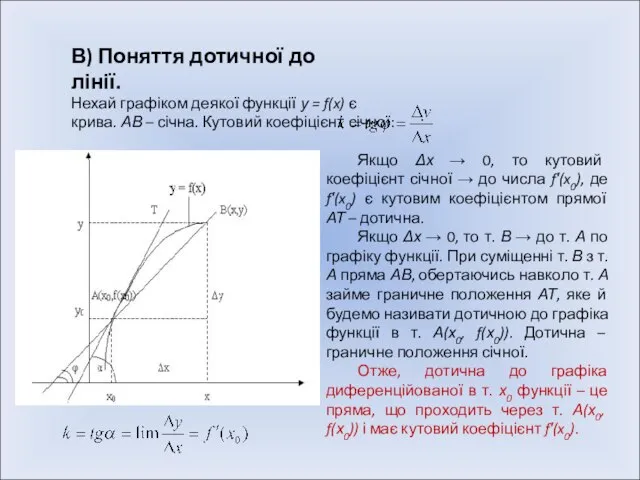
В) Поняття дотичної до лінії.
Нехай графіком деякої функції у = f(x) є крива. АВ – січна. Кутовий коефіцієнт січної:
Якщо Δх → 0, то кутовий коефіцієнт січної → до числа f′(x0), де f′(x0) є кутовим коефіцієнтом прямої АТ – дотична.
Якщо Δх → 0, то т. В → до т. А по графіку функції. При суміщенні т. В з т. А пряма АВ, обертаючись навколо т. А займе граничне положення АТ, яке й будемо називати дотичною до графіка функції в т. А(х0, f(х0)). Дотична – граничне положення січної.
Отже, дотична до графіка диференційованої в т. х0 функції – це пряма, що проходить через т. А(х0, f(х0)) і має кутовий коефіцієнт f′(x0).
.
.

Г) Виведення рівняння дотичної до графіка функції
в даній точці
Виведемо рівняння дотичної до графіка диференційованої функції
у = f(x) в т. А(х0, f(х0)).
Рівняння прямої з кутовим коефіцієнтом k має вигляд: .
Дотична – це пряма з кутовим коефіцієнтом k = f′(x0), отже її рівняння:
(1)
Для обчислення b скористаємося тим, що дотична проходить
через т. А(х0, f(х0)), отже координати т. А задовольняють рівняння (1):
f(х0) = f′(x0) х0 + b, звідки b = f(х0) – f′(x0) х0.
Підставимо в рівняння (1), отримаємо:
у = f′(x0) х + f(х0) – f′(x0) х0 = f′(x0)(х – х0) + f(х0).
Отже, рівняння дотичної:

ІІІ. Набуття навичок складання рівняння
дотичної до графіка даної функції в даній точці
Написати рівняння дотичної до графіка функції
в т. х0 = 2
Розв’язування
Рівняння дотичної обчислюємо за формулою:
Складаємо алгоритм знаходження рівняння дотичної:
1). Знаходимо значення функції в т. :
f(х0) = f(2) = 23 – 2 ּ22 + 1 = 8 – 8 +1 = 1; f(х0) = 1.
2). Знаходимо похідну функції:
.
3). Знаходимо значення функції похідної в т. х0 = 2:
f′(x0) = f′(2) =3ּ22 –4⋅2=12–8=4 ; f′(x0) = 4.
4). Отже, рівняння дотичної:
у = 4 (х – 2) + 1 = 4х –8 + 1 = 4х –7.
Відповідь: у = 4х –7.

2. Написати рівняння дотичної до графіка функції в т. х0 = 5.
Розв’язування
1) g(x0) = g(5) = ; g(x0) = 3.
2) g′(x) =
3) g′(x0) = g′(5) = ; g′(x0) = .
4) у =
Відповідь: у = .
.

ІV. Самостійна робота.
Написати рівняння дотичної до графіка функції в точці з абсцисою х0
1. f(x) = х3 + 3х в т. х0 = –1. 1. g(x) = 2х3 – 3х в т. х0 = 1.
2. g(x) = в т. х0 = 3. 2. f(x) = в т. х0 = 2.
3*. f(x) = в т. х0 = 4. 3*. h(x) = в т. х0 = 2.
Додатково: С – 30, В – 6 і В – 7.
Написати рівняння дотичної до графіка функції в точці з абсцисою х0:
у = sin 2x в т. . 1. у = в т. .
у = в т. х0 = –2. 2. у = х2 – 2х в т. х0 = 2.
(Виконати мал.)
Додатково: С – 30, В – 1 і В –2.

Написати рівняння дотичної до графіка функції в точці з абсцисою х0
1. у = х –1. 1. у = 3х –4.
2. у = 2х – 4. 2.
3*. у = 4х – 7 3*. h = 4х – 7
Написати рівняння дотичної до графіка функції в точці з абсцисою х0:
у = . 1. у = 2х – 4
у = –0,5х –2 2. у = 2х – 4
Відповіді