Древнегреческая математика

Понятие древнегреческая математика охватывает достижения грекоязычных математиков, живших в период между VI веком до н. э. и V веком н. э.
Начальный период
Вплооть до VI века до н.э. греческая математика ничем выдающимся не прославилась.
В VI века до н.э. Появляются сразу две научные школы – ионийцы (Фалес Милетский, Анаксимен, Анаксимандр) и пифагорейцы.
Фалес хорошо изучил вавилонскую математику и астрономию. Ионийцы дали первые доказательства геометрических теорем.
Однако главная роль в деле создания античной математики принадлежит пифагорейцам
Пифагорейская школа.
В 530 г до г.э. в городе Кротон основал нечто вроде тайного духовного ордена. Пифагорейские школы появились в Афинах, на остовах и в греческих колониях, а их математические знания, строго оберегаемые от посторонних, сделались общим достоянием.
Пифагорейцы занимались астрономией, геометрией, арифметикой, создали теорию музыки. Геометрия пифагорейцев ограничивалась планиметрией и завершалась доказательством «теоремы Пифагора».
Была построена математическая теория музыки.

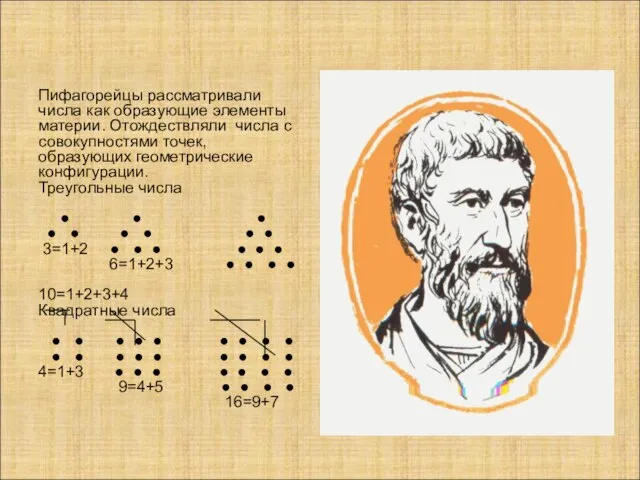
Пифагорейцы рассматривали числа как образующие элементы материи. Отождествляли числа с совокупностями точек, образующих геометрические конфигурации.
Треугольные числа
● ● ●
● ● ● ● ● ●
3=1+2 ● ● ● ● ● ●
6=1+2+3 ● ● ● ●
10=1+2+3+4
Квадратные числа
● ● ● ● ● ● ● ● ●
● ● ● ● ● ● ● ● ●
4=1+3 ● ● ● ● ● ● ●
9=4+5 ● ● ● ●
16=9+7

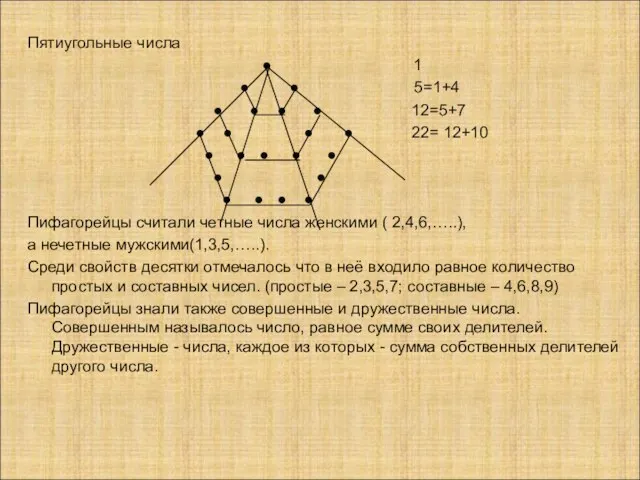
Пятиугольные числа
● 1
● ● 5=1+4
● ● ● ● 12=5+7
● ● ● ● 22= 12+10
● ● ● ● ●
● ●
● ● ● ●
Пифагорейцы считали четные числа женскими ( 2,4,6,…..),
а нечетные мужскими(1,3,5,…..).
Среди свойств десятки отмечалось что в неё входило равное количество простых и составных чисел. (простые – 2,3,5,7; составные – 4,6,8,9)
Пифагорейцы знали также совершенные и дружественные числа. Совершенным называлось число, равное сумме своих делителей. Дружественные - числа, каждое из которых - сумма собственных делителей другого числа.

Рафаэль Санти. Пифагор (деталь Афинской школы)

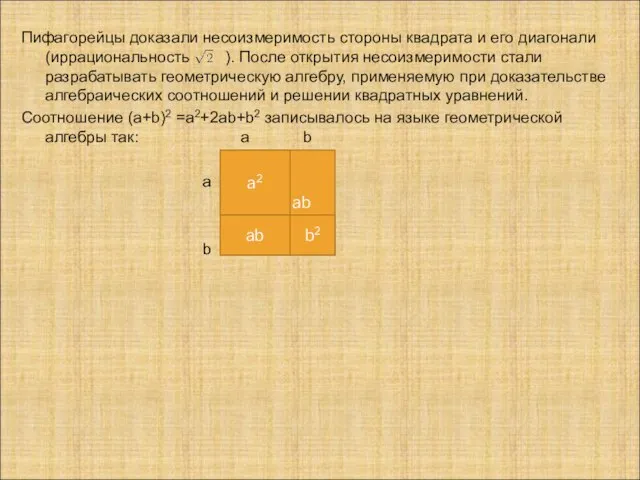
ab
Пифагорейцы доказали несоизмеримость стороны квадрата и его диагонали (иррациональность ). После открытия несоизмеримости стали разрабатывать геометрическую алгебру, применяемую при доказательстве алгебраических соотношений и решении квадратных уравнений.
Соотношение (a+b)2 =a2+2ab+b2 записывалось на языке геометрической алгебры так: a b
a
b
a2
b2
ab

V век до н.э. Зенон , Демокрит
Зенон Элейский высказал более 40 парадоксов из
которых наиболее знамениты четыре. Они до сих пор
служат предметом серьёзного анализа. В них затронуты
самые деликатные вопросы оснований математики –
конечность и бесконечность, непрерывность и
дискретность.
В конце V века до н.э. жил ещё один выдающийся
мыслитель Демокрит. Знаменит созданием
концепции атомов. Нашёл объём пирамиды и
конуса, но доказательство своих формул не дал.

IV век до н.э. – Платон , Евдокс
В 389 году до н.э. Платон основал в Афинах свою
школу – Академию. Сам Платон конкретно
Математических исследований не вёл, но
опубликовал глубокие рассуждения по философии
и методологии математики.
Евдокс Книдский
Ему принадлежат два самых выдающихся открытия: общая теория отношений (геометрическая модель вещественных чисел) и античный анализ – метод исчерпывания.

Евклид- один из великих геометров древности.
Главный труд «Начала» (13 книг), содержащий
основы античной математики, элементарной
геометрии, теории чисел, общей теории
отношений и метода определения площадей
и объемов, включавшего элементы теории
пределов, оказал огромное влияние на развитие
математики.
Им были сформулированы все задачи
эквивалентные квадратным уравнениям. Все они
Решались геометрически.
1)x2=ab
2)x(a-x)=S
3)(a+x)x=s
Способ решения задач второго типа
x(a-x)=S
S=b2
x(a-x)=b2 A E D E` B
1)AB=a
2)AD=DB
CDB=90o CD=b A` B`
Окружность R=DB С
с центром в точке С
5) x=EA Строим
Прямоугольник со
сторонами АВ и х

1 книга. Теорема Пифагора.

Греческая математика поражает прежде всего красотой и богатством содержания. Два достижения греческой математики далеко пережили своих творцов.
Первое - греки построили математику как целостную науку с собственной методологией, основанной на чётко сформулированных законах логики.
Второе - они провозгласили, что законы природы постижимы для человеческого разума, и математические модели - ключ к их познанию.
В этих двух отношениях античная математика вполне современна.
Заключение