Движение на плоскости

МОЖНО ЛИ ПЕРЕМЕЩАТЬ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ НА ПЛОСКОСТИ?

ДВИЖЕНИЕ

ЧТО ТАКОЕ ДВИЖЕНИЕ?
Движение – Отражение плоскости на себя, которое сохраняет расстояние между точками
?

СУЩЕСТВУЕТ 4 ВИДА
ДВИЖЕНИЯ
СИММЕТРИЯ ОТНОСИТЕЛЬНО ТОЧКИ
СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ
ПОВОРОТ вокруг точки
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС на вектор
назад

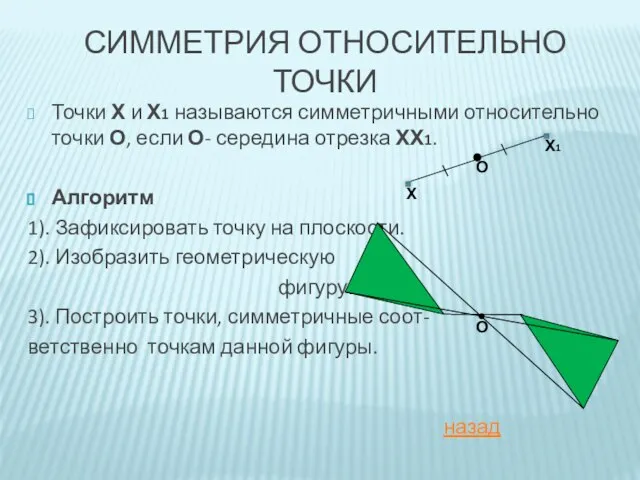
Точки Х и Х1 называются симметричными относительно точки О, если О- середина отрезка ХХ1.
Алгоритм
1). Зафиксировать точку на плоскости.
2). Изобразить геометрическую
фигуру.
3). Построить точки, симметричные соот-
ветственно точкам данной фигуры.
СИММЕТРИЯ ОТНОСИТЕЛЬНО ТОЧКИ
О
Х1
Х
О
назад

ЦЕНТРАЛЬНО-СИММЕТРИЧНЫЕ ФИГУРЫ
Если симметрия относительно точки О отображает фигуру на себя, то такая фигура называется центрально-симметричной, а точка О- ее центром симметрии.
пример
назад

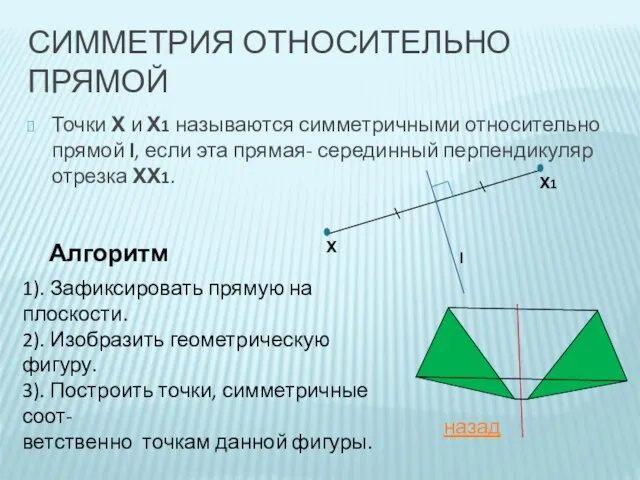
СИММЕТРИЯ ОТНОСИТЕЛЬНО ПРЯМОЙ
Точки Х и Х1 называются симметричными относительно прямой l, если эта прямая- серединный перпендикуляр отрезка ХХ1.
1). Зафиксировать прямую на плоскости.
2). Изобразить геометрическую фигуру.
3). Построить точки, симметричные соот-
ветственно точкам данной фигуры.
Алгоритм
Х
Х1
l
назад

ФИГУРЫ СИММЕТРИЧНЫЕ ОТНОСИТЕЛЬНО ПРЯМОЙ
Если симметрия относительно прямой l отображает фигуру на эту же фигуру, то данная фигура называется симметричной относительно прямой, а прямая l- ее осью симметрии.
пример
назад

Примером центрально-симметричной фигуры является параллелограмм.
Центром симметрии параллелограмма является точка пересечения его диагоналей.
О
назад

Примерами таких фигур являются ромб, квадрат, прямоугольник, окружность и т.д.
Прямые, на которых лежат диагонали ромба,- его оси симметрии.
Обратите внимание:
Ромб и прямоугольник имеют по 2 оси симметрии
Квадрат- 4 оси симметрии
Окружность – бесконечно много
назад

ПРОЦЕСС СМЕЩЕНИЯ КАКИМ-НИБУДЬ ОБРАЗОМ КАЖДОЙ ТОЧКИ ФИГУРЫ, ПРИ КОТОРОМ МЫ ПОЛУЧАЕМ НОВУЮ ФИГУРУ, НАЗЫВАЕТСЯ ГЕОМЕТРИЧЕСКИМ ПРЕОБРАЗОВАНИЕМ.
НАЗАД

ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что вектор ММ1 равен вектору а
Алгоритм
1). Изобразить геометрическую фигуру.
2). Каждую ее точку сместить в одном и том же направлении(по сонаправленным лучам) на одно и то же расстояние.
а
М
М1
N
N1
назад

ПОВОРОТ
Поворотом плоскости вокруг точки О на угол α называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что ОМ=ОМ1 и угол МОМ1 равен α
F
F1
О
Алгоритм
1). Зафиксировать точку на плоскости.
2). Изобразить геометрическую фигуру.
3). Повернуть каждую точку этой фигуры около точки О на угол α.
Обратите внимание. Симметрию относительно точки О можно определить так же , как поворот на 180° около этой точки.
О
М1
М
α
назад

Рассмотрим задачу с готовым решением.

Задача. Угол большой прямоугольной комнаты требуется отгородить двумя небольшими одинаковыми ширмами. Как следует расположить ширмы, чтобы отгороженная площадь была наибольшей?
Решение. Построим фигуру, центрально-симметричную ширмам относительно вершины угла комнаты, а также фигуры, симметричные ширмам относительно стен.
В результате получится восьмиугольник, периметр
которого в восемь раз больше длины ширмы, а площадь
в четыре раза больше отгороженной площади. Но, как
мы знаем, из всех n- угольников c данным периметром
наибольшую площадь имеет правильный n- угольник.
Поэтому и отгороженная площадь будет наибольшей в том
случае, когда ширмы будут расположены симметрично
Относительно биссектрисы угла комнаты, а угол между
Ними будет равен углу правильного восьмиугольника, т.е.
Равен 135°.