Содержание
- 2. Цель лекции Изучить теоретические основы двоичных деревьев поиска и очереди с приоритетами и алгоритмы их обработки
- 3. Постановка задачи Реализовать структуру данных, хранящую набор чисел и поддерживающую операции: добавить число найти число удалить
- 4. Двоичное дерево Дерево, каждая вершина которого имеет не более двух детей На детях каждой вершины задан
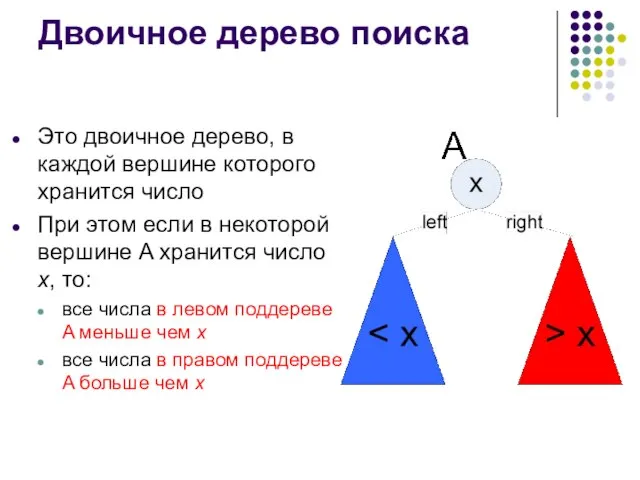
- 5. Двоичное дерево поиска Это двоичное дерево, в каждой вершине которого хранится число При этом если в
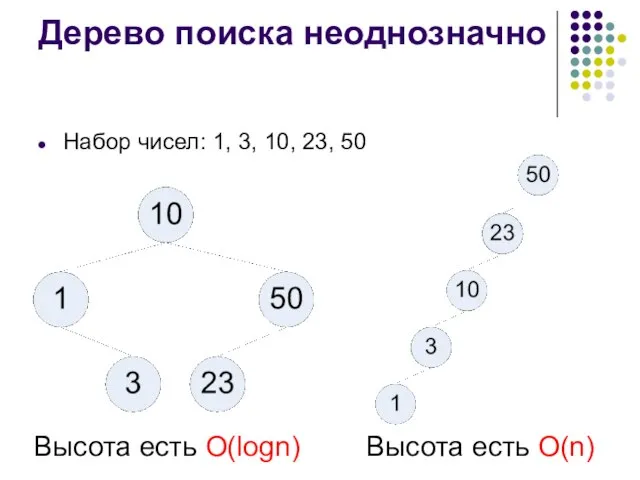
- 6. Дерево поиска неоднозначно Набор чисел: 1, 3, 10, 23, 50 Высота есть O(logn) Высота есть O(n)
- 7. Вершина дерева node = record data : integer; left, right : integer; // при реализации //
- 8. Поиск элемента в дереве Если значение y в текущей вершине равно искомому x, то поиск завершен
- 9. Программа function find(x : integer) : boolean; begin cur := root; // root – корень дерева
- 10. Поиск минимума и максимума Минимум – самый левый элемент в дереве Максимум – самый правый элемент
- 11. Добавить число Необходимо: Найти место, в котором должно находиться число Создать новый узел дерева и поместить
- 12. Программа (1) function add(root, x : integer) : integer; begin if (root = -1) then begin
- 13. Программа (2) if (x cur := add(memory[root].left, x); memory[root].left := cur; result := root; exit; end;
- 14. Вызов процедуры root := add(root, x); Здесь root – это корень дерева.
- 15. Удаление элемента Необходимо найти элемент Три случая: вершина является листом – просто удаляем у вершины один
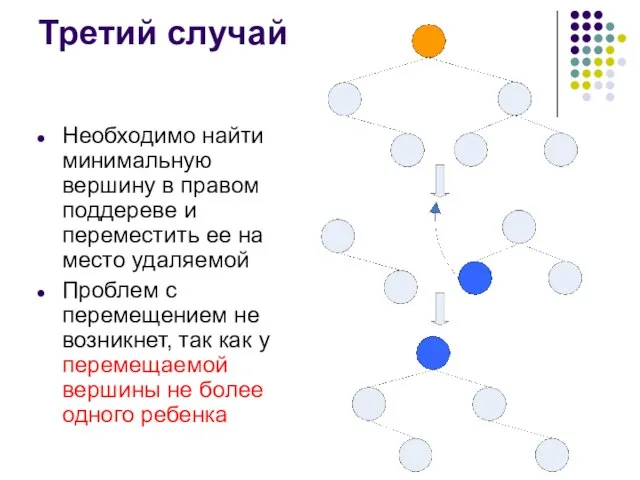
- 16. Третий случай Необходимо найти минимальную вершину в правом поддереве и переместить ее на место удаляемой Проблем
- 17. Время работы операций Время работы всех рассмотренных операций пропорционально высоте дерева – в худшем случае есть
- 18. Упражнение Предложить алгоритм нахождения следующего и предыдущего элемента в двоичном дереве поиска со временем работы пропорциональным
- 19. Поиск k-ой порядковой статистики В каждом узле дерева необходимо хранить дополнительную информацию – число узлов в
- 20. Поиск k-ого элемента Дано: Корень дерева Число k Если в левом поддереве не меньше, чем k
- 21. Программа function getKth(root, k : integer) : integer; begin sizeLeft := 0; if (memory[root].left -1) then
- 22. Упражнение Модифицировать операции добавления и удаления вершины, так чтобы они обновляли значения поля «размер поддерева». Время
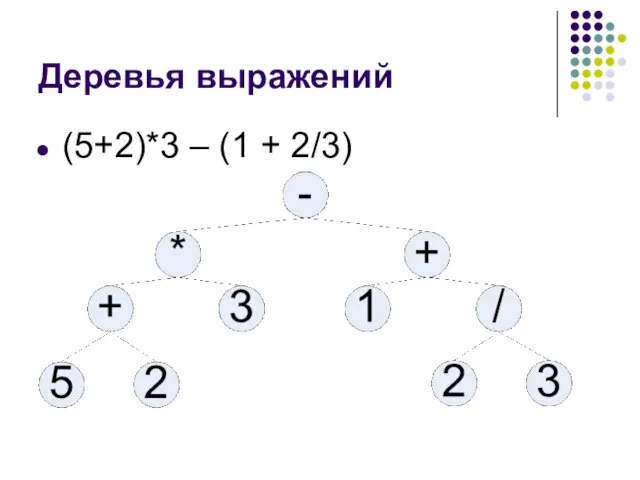
- 23. Деревья выражений (5+2)*3 – (1 + 2/3)
- 24. Обходы двоичных деревьев Основные варианты обхода двоичного дерева: корень – левое поддерево – правое поддерево левое
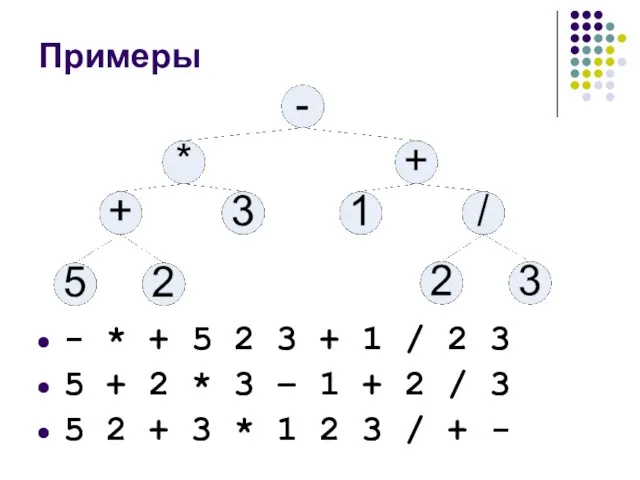
- 25. Примеры - * + 5 2 3 + 1 / 2 3 5 + 2 *
- 26. Упражнения Предложить алгоритм вычисления выражений, заданных в постфиксной записи (указание: используйте стек) Применение какого из обходов
- 27. Очередь с приоритетами Структура данных с двумя операциями: добавить элемент и назначить ему приоритет извлечь элемент
- 28. Простая реализация Храним массив записей element = record data, priority : integer; end; Добавление – в
- 29. Структура данных «куча» Полное двоичное дерево Хранится в массиве: Левый ребенок – 2 * i Правый
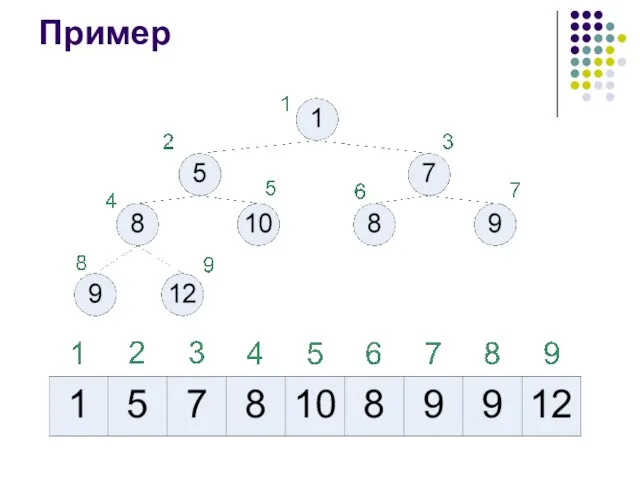
- 30. Пример
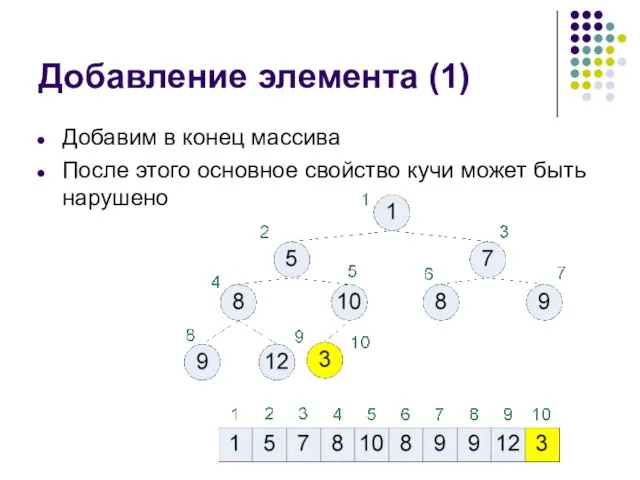
- 31. Добавление элемента (1) Добавим в конец массива После этого основное свойство кучи может быть нарушено
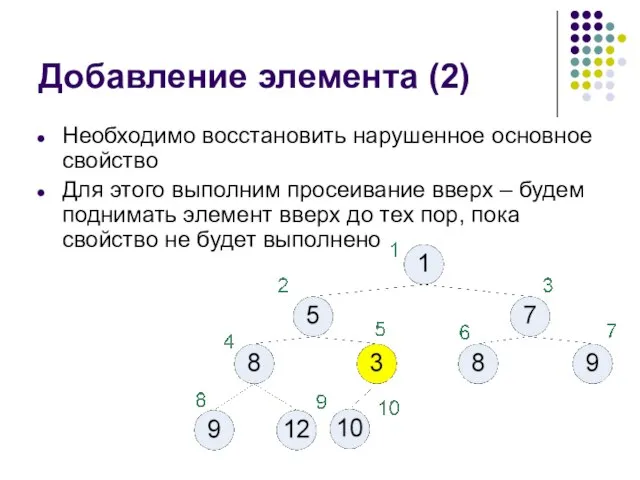
- 32. Добавление элемента (2) Необходимо восстановить нарушенное основное свойство Для этого выполним просеивание вверх – будем поднимать
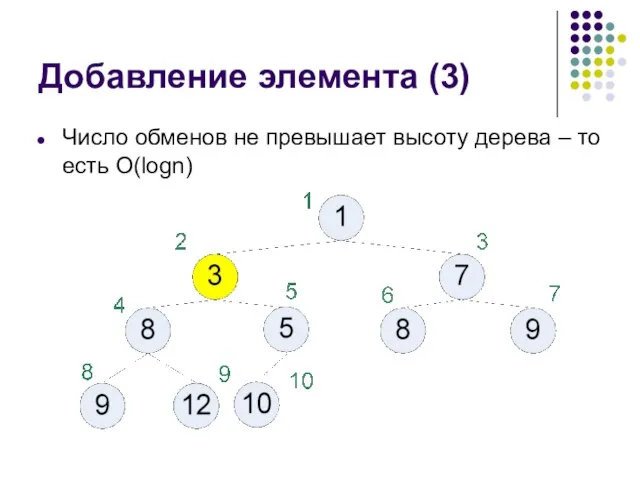
- 33. Добавление элемента (3) Число обменов не превышает высоту дерева – то есть O(logn)
- 34. Добавление элемента (4) procedure add(x : integer); begin inc(size); heap[size] := x; i := size; while
- 35. Извлечение элемента (1) Минимальный элемент находится на вершине кучи Поменяем его местами с последним и удалим
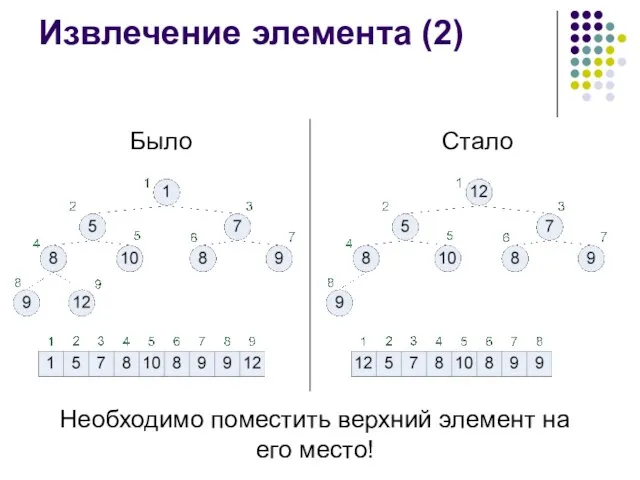
- 36. Извлечение элемента (2) Было Стало Необходимо поместить верхний элемент на его место!
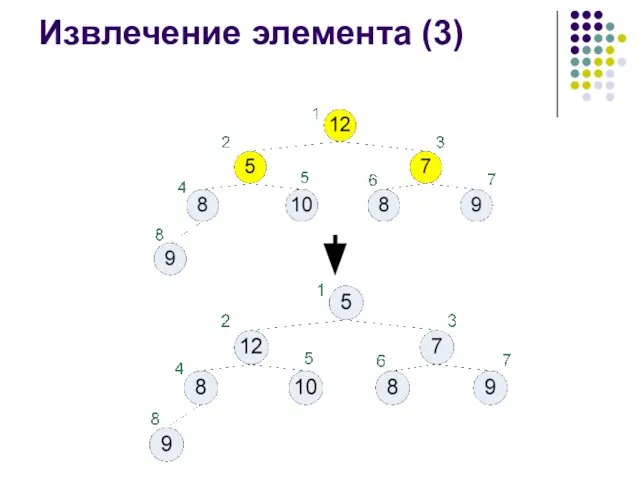
- 37. Извлечение элемента (3)
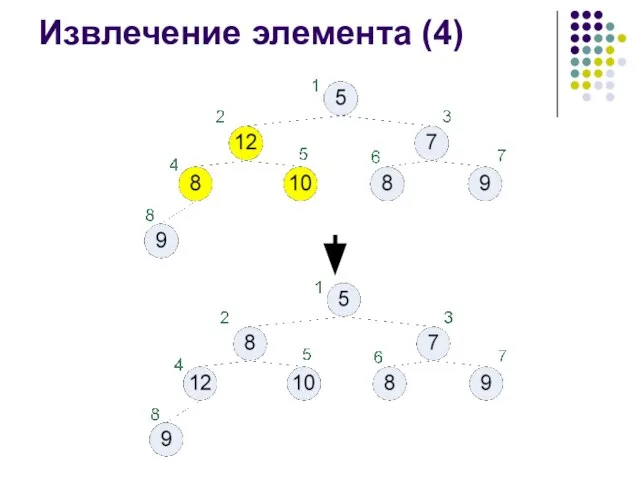
- 38. Извлечение элемента (4)
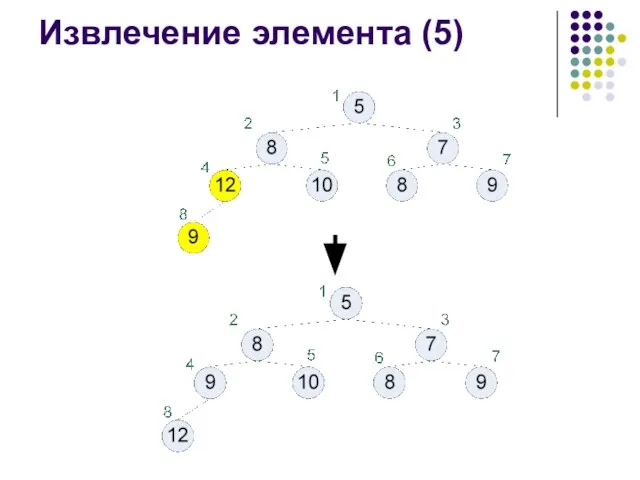
- 39. Извлечение элемента (5)
- 40. Извлечение элемента (5) function remove() : integer; begin result := heap[1]; heap[1] := heap[size]; dec(size); i
- 41. Сортировка с помощью кучи Можно добавить все элементы массива в кучу, а потом по очереди извлечь
- 42. Построение кучи из массива for i := n div 2 downto 1 do begin siftDown(i); end;
- 43. Время работы Грубая оценка – O(nlogn) Более точная оценка – O(n)
- 44. Построение упорядоченного массива из кучи for j := 1 to n do begin swap(heap[1], heap[size]); dec(size);
- 45. Время работы heapSort Общее время работы heapSort есть O(n + nlogn) = O(nlogn)
- 46. Выводы Двоичные деревья поиска позволяют быстро выполнять словарные операции при условии, что у них небольшая высота
- 48. Скачать презентацию









![Программа (2) if (x cur := add(memory[root].left, x); memory[root].left := cur; result](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/388267/slide-12.jpg)













![Добавление элемента (4) procedure add(x : integer); begin inc(size); heap[size] := x;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/388267/slide-33.jpg)

![Извлечение элемента (5) function remove() : integer; begin result := heap[1]; heap[1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/388267/slide-39.jpg)






 Время и календарь
Время и календарь Методические рекомендации по организации портфолио по курсу «Юридическая психология»
Методические рекомендации по организации портфолио по курсу «Юридическая психология» Яркие представители мира динозавров
Яркие представители мира динозавров Тип кольчатые черви 7 класс
Тип кольчатые черви 7 класс Дизайн и реклама – составляющие художественной культуры
Дизайн и реклама – составляющие художественной культуры Рождение капитализма (новый общественный строй)
Рождение капитализма (новый общественный строй) Сущность и принципы маркетинга
Сущность и принципы маркетинга Древние мифы, легенды, сказки, предания, благожеланиея дальневосточной земли.
Древние мифы, легенды, сказки, предания, благожеланиея дальневосточной земли. Всероссийский День правовой помощи детям. Права человека
Всероссийский День правовой помощи детям. Права человека Талант помогает исправиться
Талант помогает исправиться Зинин
Зинин Urok_11
Urok_11 Политическое поведение
Политическое поведение Спорт в Британии
Спорт в Британии Таможенное оформление круизных лайнеров и их пассажиров
Таможенное оформление круизных лайнеров и их пассажиров «Построение маркетинговых коммуникаций с молодёжной аудиторией в соответствии с её образом жизни и моделью потребления»
«Построение маркетинговых коммуникаций с молодёжной аудиторией в соответствии с её образом жизни и моделью потребления» Виды Дверей
Виды Дверей Рецепция римского права
Рецепция римского права 幅作品. 戴花的惠安阿婆
幅作品. 戴花的惠安阿婆 Основы научных исследований и инновационной деятельности
Основы научных исследований и инновационной деятельности “Fried Green Tomatoes at the Whistle Stop Café”
“Fried Green Tomatoes at the Whistle Stop Café” Синяя лента апреля
Синяя лента апреля Формы и системы оплаты труда на предприятиях
Формы и системы оплаты труда на предприятиях КАК ОРГАНИЗОВАТЬ КОНКУРС КИО В ШКОЛЕ
КАК ОРГАНИЗОВАТЬ КОНКУРС КИО В ШКОЛЕ Числа с собственными именами
Числа с собственными именами Послеоперационный период
Послеоперационный период  Программа amoCRM
Программа amoCRM Реализация PR и IR стратегий: особенности национального информационного поля
Реализация PR и IR стратегий: особенности национального информационного поля