Двугранный угол

Вдохновение есть расположение души к живейшему принятию впечатлений и соображению понятий, следственно, и объяснению оных. Вдохновение нужно в геометрии, как и в поэзии.
А.С. Пушкин

геометрия

угол

двугранный

знакомство с понятиями двугранный угол и его линейный угол, обучение построению линейного угла данного двугранного угла, развитие навыков построения перпендикуляра к плоскости, применения ТТП, внимания,
воспитание усидчивости, взаимоуважения.
получить необходимую информацию;
проанализировать полученную информацию;
применить теорию на практике;
заполнить кластер;
оценить свою деятельность.

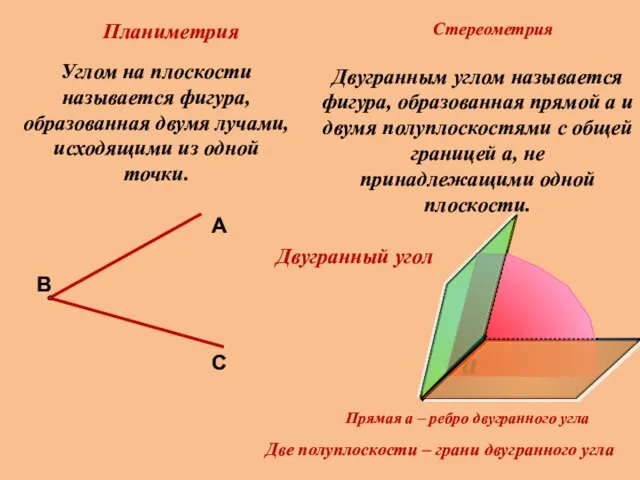
Планиметрия
Стереометрия
Углом на плоскости называется фигура, образованная двумя лучами, исходящими из одной точки.
Двугранный угол
Двугранным углом называется фигура, образованная прямой a и двумя полуплоскостями с общей границей a, не принадлежащими одной плоскости.
а
Прямая a – ребро двугранного угла
Две полуплоскости – грани двугранного угла

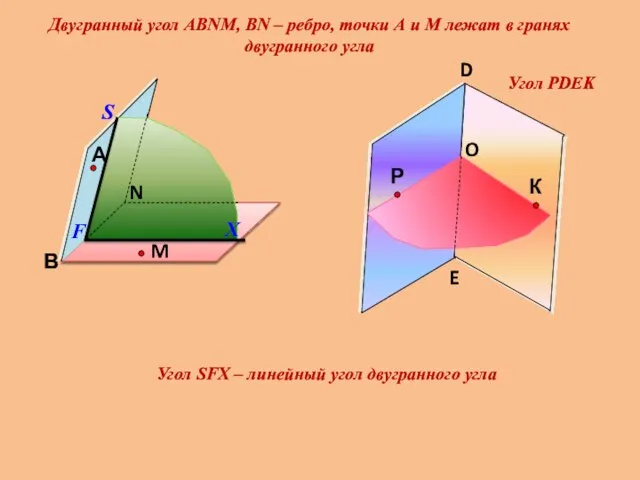
Угол РDEK
Двугранный угол АВNМ, ВN – ребро, точки А и М лежат в гранях двугранного угла
А
В
N
Р
M
К
D
E
Угол SFX – линейный угол двугранного угла

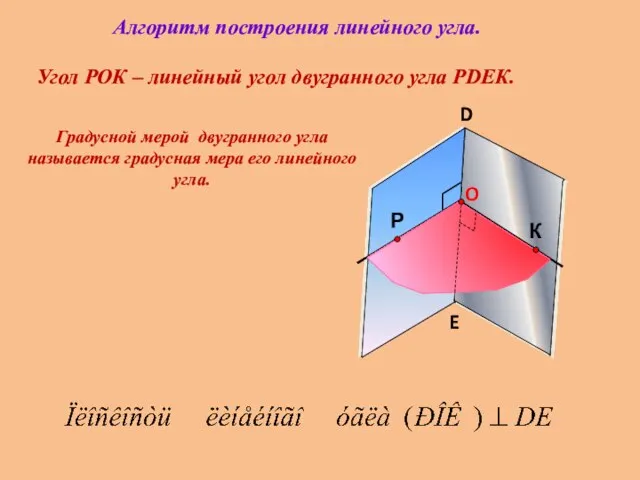
Угол РОК – линейный угол двугранного угла РDEК.
D
E
Градусной мерой двугранного угла называется градусная мера его линейного угла.
Алгоритм построения линейного угла.

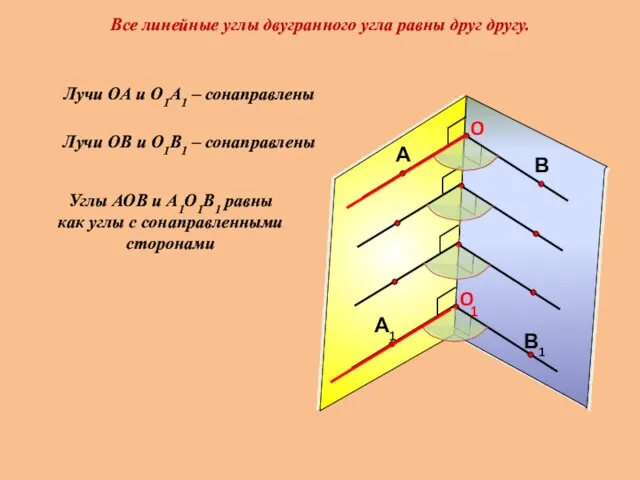
Все линейные углы двугранного угла равны друг другу.
1
Лучи ОА и О1А1 – сонаправлены
Лучи ОВ и О1В1 – сонаправлены
Углы АОВ и А1О1В1 равны
как углы с сонаправленными сторонами

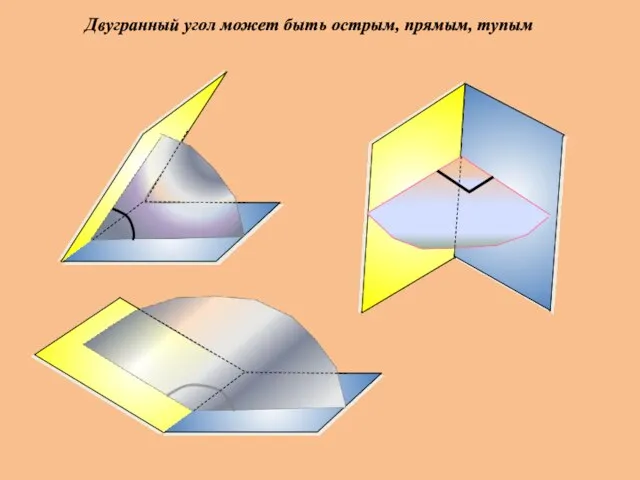
Двугранный угол может быть острым, прямым, тупым

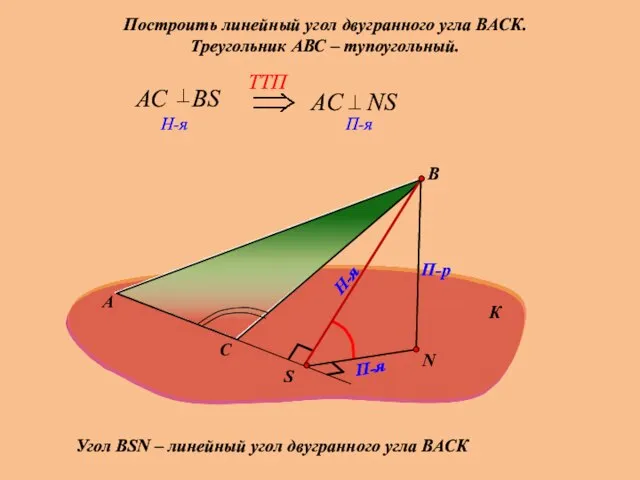
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – тупоугольный.
А
В
П-р
Н-я
П-я
Угол ВSN – линейный угол двугранного угла ВАСК
К
С

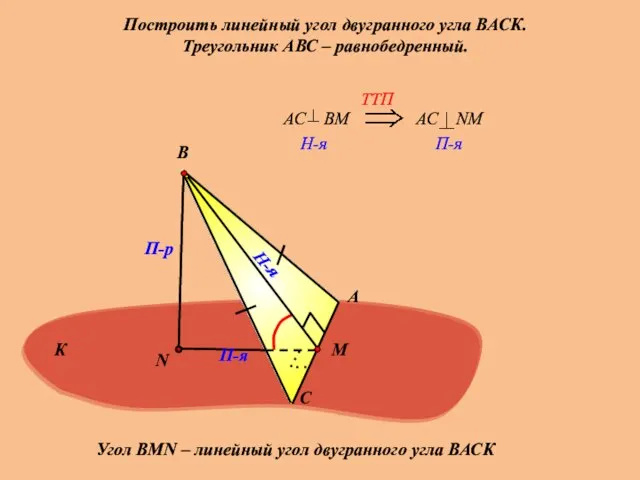
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – равнобедренный.
А
С
В
П-р
Н-я
П-я
Угол ВMN – линейный угол двугранного угла ВАСК
К

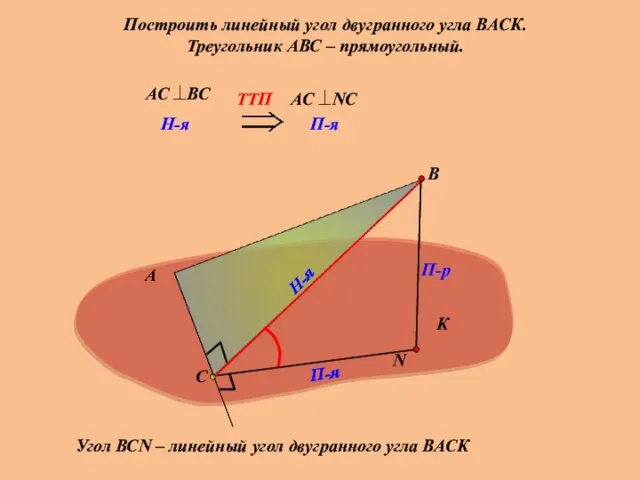
Построить линейный угол двугранного угла ВАСК.
Треугольник АВС – прямоугольный.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный угол двугранного угла ВАСК
К
С

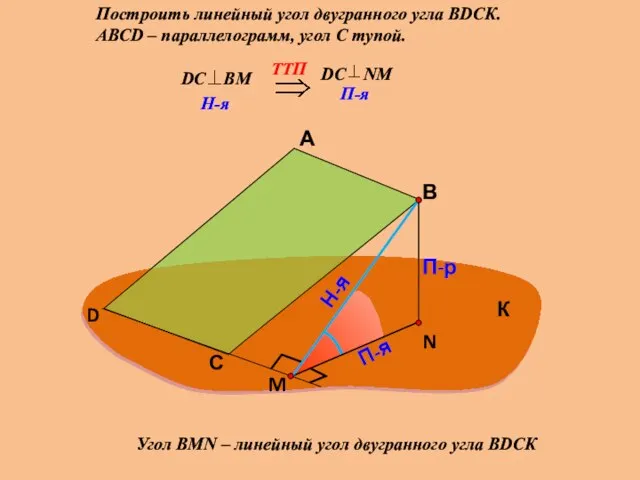
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С тупой.
А
В
П-р
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я

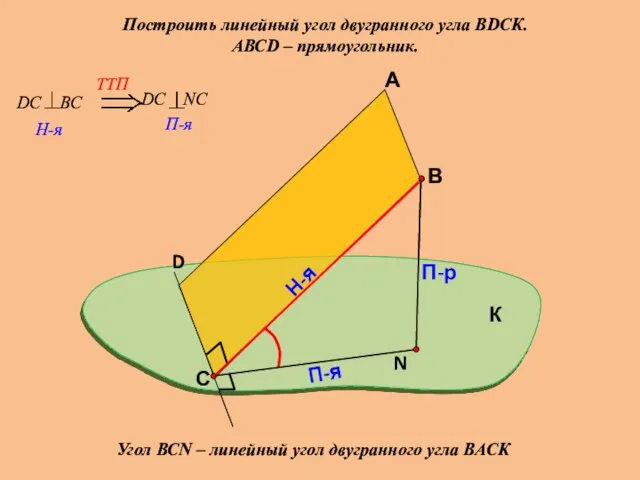
Построить линейный угол двугранного угла ВDСК.
АВСD – прямоугольник.
А
В
П-р
Н-я
П-я
Угол ВСN – линейный угол двугранного угла ВАСК
К
С
D

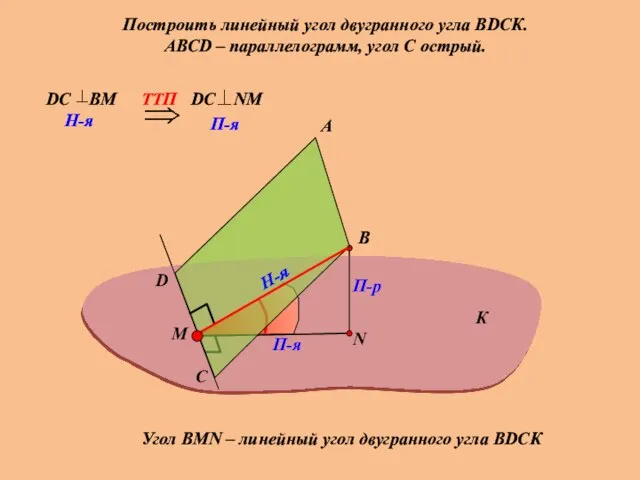
Построить линейный угол двугранного угла ВDСК.
АВСD – параллелограмм, угол С острый.
А
В
П-р
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я

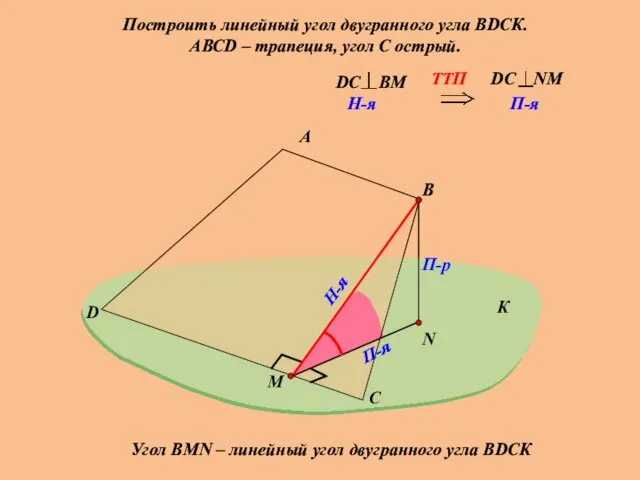
Построить линейный угол двугранного угла ВDСК.
АВСD – трапеция, угол С острый.
А
В
П-р
П-я
Угол ВMN – линейный угол двугранного угла ВDСК
К
С
D
Н-я

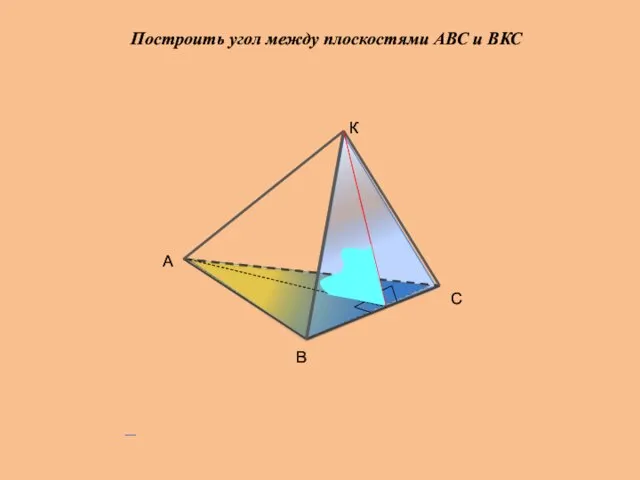
Построить угол между плоскостями АВС и ВКС

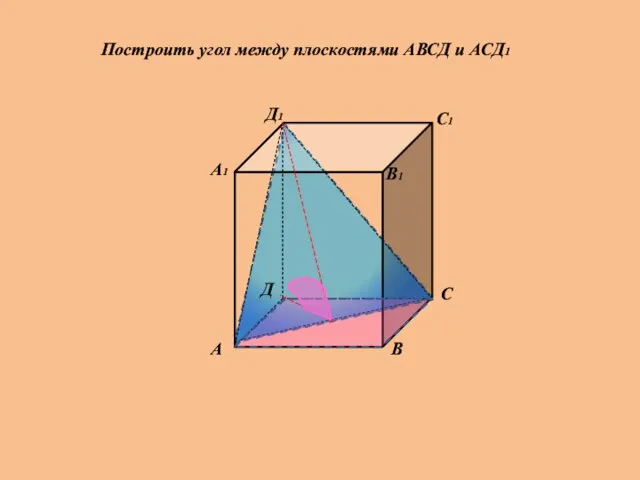
А1
В1
С1
Д1
А
В
С
Д
Построить угол между плоскостями АВСД и АСД1

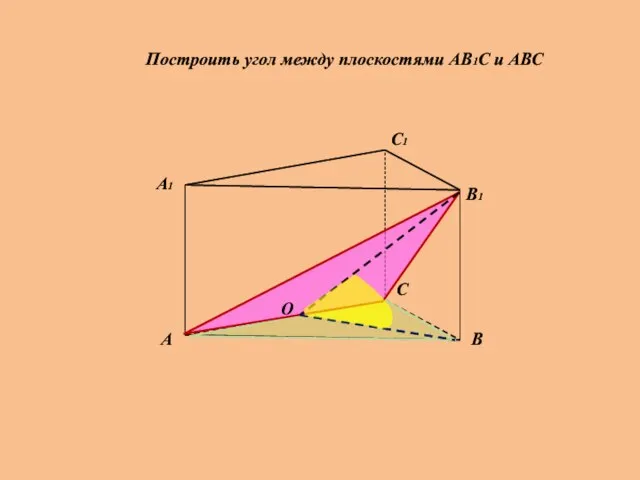
Построить угол между плоскостями АВ1С и АВС
А
А1
В
В1
С
С1
О

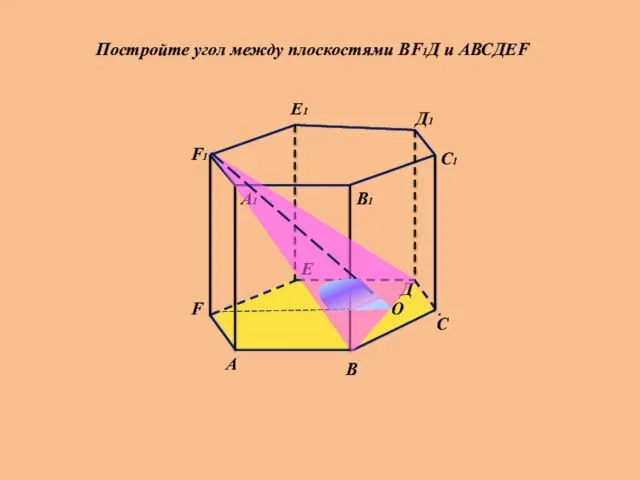
А
А1
В
В1
С
С1
О
Д
Д1
Е
Е1
F
F1
Постройте угол между плоскостями ВF1Д и АВСДЕF

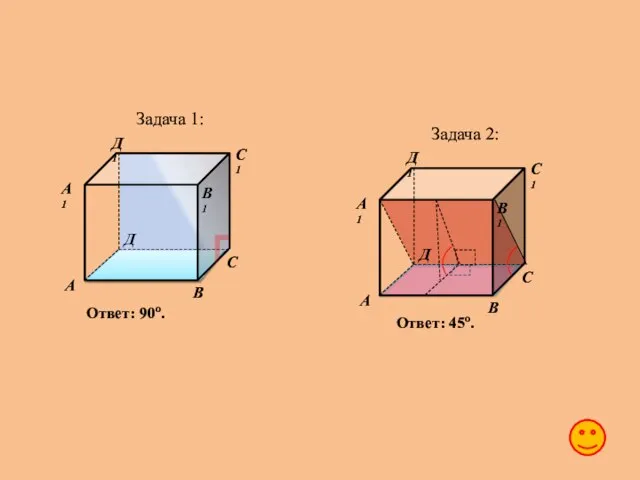
Задача 1:
В кубе A…D1 найдите угол между плоскостями ABC и CDD1. В кубе A…D1 найдите угол между плоскостями ABC и CDA1.
Задача 2:
Задача 3:
В кубе A…D1 найдите угол между плоскостями ABC и BDD1.
Задача 4:
В кубе A…D1 найдите угол между плоскостями ACC1 и BDD1.
В кубе A…D1 найдите угол между плоскостями BC1D и BA1D.
Задача 5:
Задача 6:

Задача 1:
Ответ: 90o.
Задача 2:
А
В
С
Д
А1
В1
С1
Д1
Ответ: 45o.

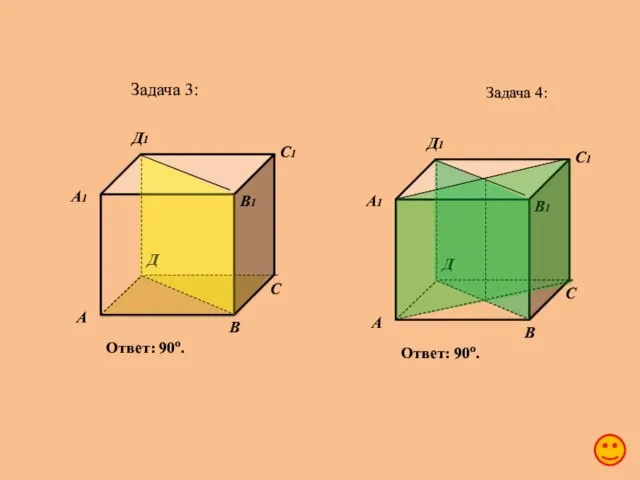
Задача 3:
А
В
С
Д
А1
В1
С1
Д1
Ответ: 90o.
Задача 4:
А
В
С
Д
А1
В1
С1
Д1
Ответ: 90o.

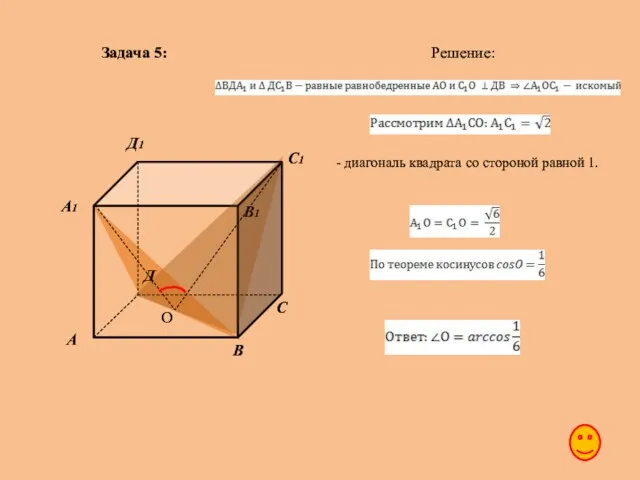
Задача 5:
Решение:
О
- диагональ квадрата со стороной равной 1.

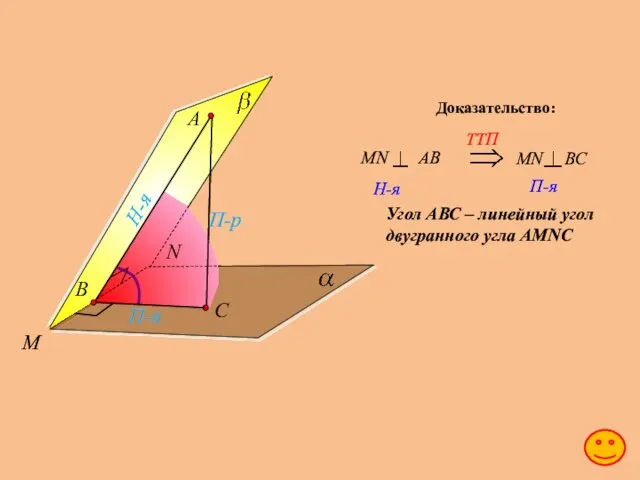
M
N
А
П-р
Н-я
П-я
Угол АВС – линейный угол двугранного угла АМNC
Доказательство:

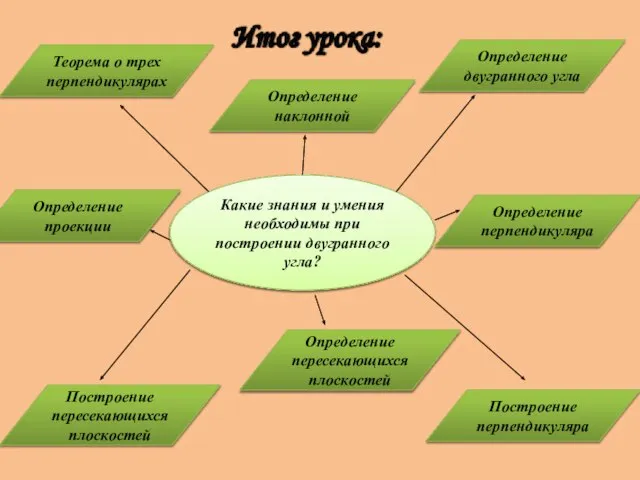
Какие знания и умения необходимы при построении двугранного угла?
Определение двугранного угла
Теорема о трех перпендикулярах
Построение перпендикуляра
Определение пересекающихся плоскостей
Построение пересекающихся плоскостей
Определение перпендикуляра
Определение наклонной
Определение проекции