Дюндюков Владислав Сергеевич Московский государственный технический университет им. Н.Э. Баумана, кафедра «Компьютерные системы

ПРЕДЫСТОРИЯ
1. Потоки в сетях (алгоритм Форда-Фалкерсона)
2. Метод и программная среда РДО (ресурсы-действия-операции) В.В. Емельянова и С.И. Ясиновского
3. Ресурсные графы О.П. Кузнецова
4. Теория агентов и МАС: представление агентов в координатах «цели-ресурсы-восприятие-действия»(Тарасов, Вулдридж, Дженнингс и др.)
5. Ресурсно-целевые графы

ОСНОВНЫЕ ПАРАМЕТРЫ ПРОЦЕССА ВЗАИМОДЕЙСТВИЯ АГЕНТОВ В МАС
1) Совместимость целей или намерений агентов;
2) Отношение агентов к ресурсам и величина имеющихся у них ресурсов, потребность в дополнительных ресурсах и совместном использовании ресурсов;
3) Опыт агентов, связанный с некоторой проблемной областью;
4) Обязательства агентов друг перед другом.
В работе главное внимание уделяется исследованию и моделированию взаимосвязей между типами агентов, характером формируемых или принимаемых ими целей и ситуациями обмена (совместного использования) ресурсов.

РЕСУРСЫ В МНОГОАГЕНТНЫХ СИСТЕМАХ
Под ресурсами понимаются любые средства, полезные для достижения цели агента или МАС. Величина имеющегося у агента ресурса тесно связана с такими характеристиками как роль агента и взаимосвязи между ролями. Создание и функционирование МАС предполагает построение семейства процедур распределения, перераспределения и коллективного использования ресурсов отдельных агентов.
Наиболее удобными и наглядными методами описания структур МАС являются графы, в частности взвешенные графы, с помощью которых можно легко показать ряд важных параметров агентов (ресурс, способность к обмену ресурсами и формированию коллективных целей и т.д.)

МАС КАК ПОЛИСТРУКТУРНАЯ СИСТЕМА
Любая МАС является полиструктурной и представляет собой единство экстенсивных структур, преимущественно развертывающихся в пространстве и интенсивных структур, развивающихся во времени. Например, при построении структур в виде графов и мультиграфов развертыванию экстенсивных структур соответствует добавление новых вершин в исходный граф, а развитию интенсивных структур – добавление новых дуг.
Соответственно, выделяются две основные характеристики ресурса: а) «объем ресурса» – его мера в пространстве (например, объем перерабатываемой информации, объем памяти компьютера); б) «действие ресурса» - его мера во времени.

ВИДЫ РЕСУРСОВ
Для МАС можно выделить следующие виды ресурсов:
1) Материальные ресурсы (ограниченные), для которых в МАС действует закон сохранения суммарного ресурса.
2) Информационные ресурсы (бесконечные), для которых справедливо свойство супераддитивности: ресурсы агентов в процессе обмена только увеличиваются. Поэтому суммарный ресурс МАС будет больше суммы ресурсов отдельных агентов.
Для моделирования обмена ресурсами в МАС служат ресурсные графы, предложенные О.П. Кузнецовым.

РЕСУРСНЫЙ ГРАФ В МАС
Под ресурсным графом для МАС будем понимать взвешенный ориентированный граф
G = 〈 A, C, RES, W 〉,
где A – множество вершин (агентов), С – множество дуг (связей между агентами), RES – множество ресурсов МАС, причем каждый агент ai∈A имеет определенный ресурс res(a)∈RES, W – множество проводимостей дуг c в МАС Каждой дуге сij∈С приписывается неотрицательное число wij∈W, называемое проводимостью дуги.
Расширение формализма ресурсных графов связано с введением ресурсно-целевых графов, в которых вершины характеризуются типом и объемом ресурса, а дуги – двумя видами проводимости (по целям и по ресурсам).

РЕСУРСНО-ЦЕЛЕВОЙ ГРАФ В МАС
Ресурсно-целевым графом называется взвешенный ориентированный мультиграф
G = 〈 A, C, K, O, RES, W, T 〉,
где множество вершин ассоциируется с множеством агентов A, множество дуг С разбивается на два непересекающихся подмножества: множество целевых связей СО и множество ресурсных связей СRES: С = СО∪СRES, СО∩СRES=∅, а T – множество дискретных моментов времени, t = 0,1,2, …, п.
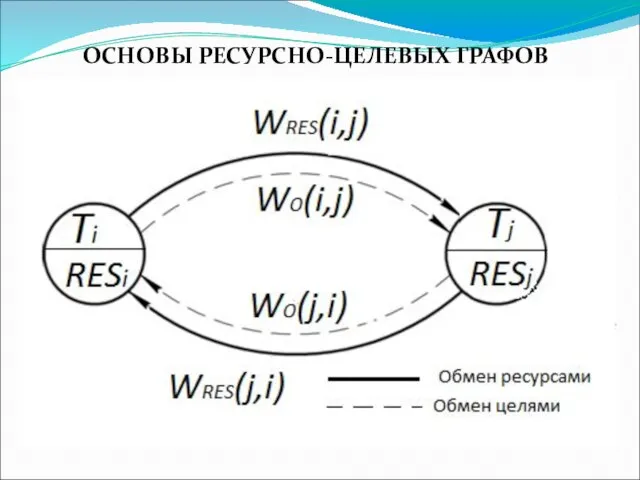
Каждая вершина a∈A определяется следующими параметрами: тип агента k∈К, его цель о(а)∈O и объем ресурса res(а)∈RES, а каждая дуга – проводимостью или пропускной способностью w дуги с∈С. У любых двух агентов ai, aj выделяются проводимости по целям wО(ai, aj) и проводимости по ресурсам wRES(ai, aj).

ОСНОВЫ РЕСУРСНО-ЦЕЛЕВЫХ ГРАФОВ

ТИПЫ АГЕНТОВ В РЕСУРСНО-ЦЕЛЕВОМ ГРАФЕ
В ресурcно-целевом графе можно выделить типы вершин на основе предварительной классификации агентов по двум критериям (благонамеренные, эгоистичные, альтруистичные и т.д.), предложенной В.Б.Тарасовым.
Благонамеренный агент ab – это агент, имеющий свои цели (интересы) и способный формировать коллективные цели. Он участвует в обмене ресурсами, если такая операция выгодна ему и другим агентам и не содержит злого умысла.
Эгоистичный агент ae стремится к достижению исключительно своих целей, игнорирует цели других агентов и неспособен к формированию общих (коллективных) целей. Он участвует в обмене ресурсами тогда и только тогда, когда этот обмен ему необходим и выгоден.
Альтруистичный агент aa – это агент, неспособный к формированию собственных целей и принимающий чужую цель как общую. Он всегда участвует в обмене ресурсами, даже если обмен будет неравнозначным, и он от него проиграет.

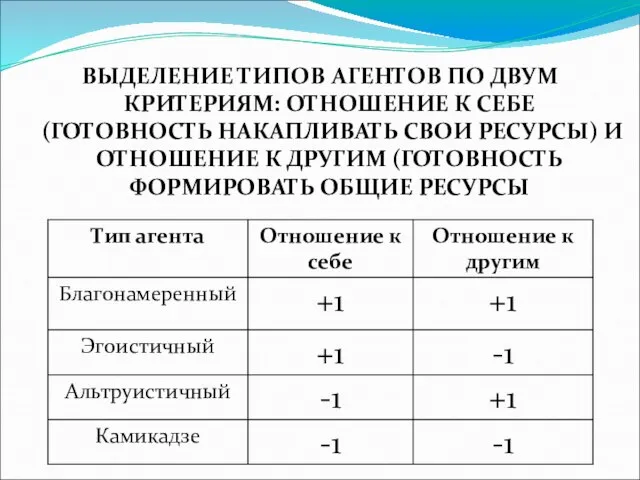
ВЫДЕЛЕНИЕ ТИПОВ АГЕНТОВ ПО ДВУМ КРИТЕРИЯМ: ОТНОШЕНИЕ К СЕБЕ (ГОТОВНОСТЬ НАКАПЛИВАТЬ СВОИ РЕСУРСЫ) И ОТНОШЕНИЕ К ДРУГИМ (ГОТОВНОСТЬ ФОРМИРОВАТЬ ОБЩИЕ РЕСУРСЫ

ОБЩАЯ СХЕМА ВОЗМОЖНЫХ ВЗАИМОДЕЙСТВИЙ МЕЖДУ АГЕНТАМИ
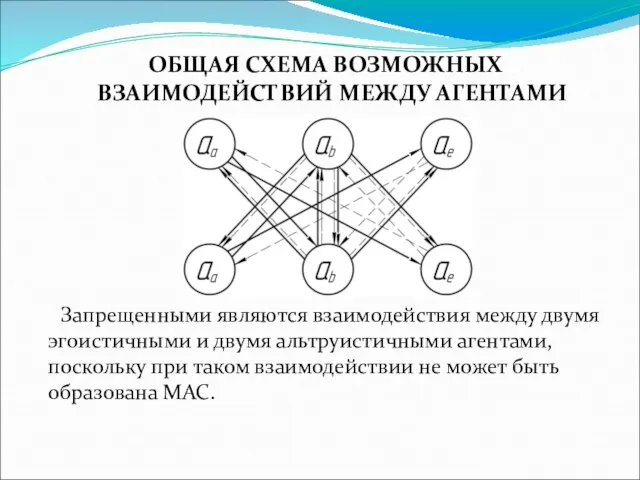
Запрещенными являются взаимодействия между двумя эгоистичными и двумя альтруистичными агентами, поскольку при таком взаимодействии не может быть образована МАС.

ПРИМЕРЫ РЕСУРСНО-ЦЕЛЕВЫХ ГРАФОВ
1) Благонамеренный агент с благонамеренным. В данной ситуации происходит равноправный обмен информацией целевого характера, в результате которого формируется общая цель, а также обмен ресурсами.
МАС, состоящая из подобных агентов, представляется наиболее эффективной для реализации стратегии децентрализованного искусственного интеллекта, когда формируется структура типа полный граф.
2) Благонамеренный агент с эгоистичным агентом.

ПРИМЕРЫ РЕСУРСНО-ЦЕЛЕВЫХ ГРАФОВ (ПРОДОЛЖЕНИЕ)
2) Эгоистичный агент с альтруистичным. При взаимодействии эгоистичный агент навязывает альтруистичному свою цель и использует для ее достижения чужие ресурсы. Фактически происходит перекачка ресурсов от aa к ae , которая может завершиться гибелью aa , если объем ресурса res(aa(t)) < res min , т.е. данная МАС будет неустойчивой

ПРИМЕРЫ РЕСУРСНО-ЦЕЛЕВЫХ ГРАФОВ (ПРОДОЛЖЕНИЕ)
3) Благонамеренный агент с эгоистичным. В данной ситуации возникает иллюзия обмена ресурсами между агентами. Эгоистичному агенту нужны ресурсы, но в ответ он старается ничего не делать. Благонамеренный агент будет избегать такого взаимодействия и участвовать в нем только в критических для себя случаях.
При этом взаимодействие прекращается, если res(ab(t)) близок к resmin (наличие «инстинкта самосохранения» у ab).

ПРИМЕРЫ РЕСУРСНО-ЦЕЛЕВЫХ ГРАФОВ (ПРОДОЛЖЕНИЕ)
4) Благонамеренный агент с альтруистичным. Происходит эффективный обмен ресурсами, причем aa разделяет цели ab. В силу своей благонамеренности ab не допускает ситуации истощения ресурсов у aa, поэтому МАС, включающая такое сочетание агентов, достаточно устойчива.

ВОЗМОЖНЫЕ ТИПЫ АГЕНТОВ В МАС
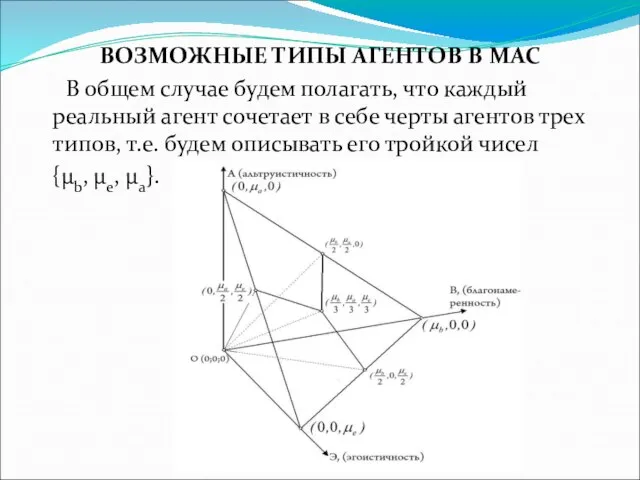
В общем случае будем полагать, что каждый реальный агент сочетает в себе черты агентов трех типов, т.е. будем описывать его тройкой чисел
{μb, μe, μa}.

ВЛИЯНИЕ АГЕНТА
В РЕСУРСНО-ЦЕЛЕВОМ ГРАФЕ
Влияние агента a в МАС определяется собственным ресурсом, числом связей с другими агентами (т.е. числом выходящих из вершины a дуг), а также суммарными значениями выходных проводимостей по целям wО и ресурсам wRES. Формально влияние агента a в момент времени t определяется имеющимся у него объемом ресурса res(а(t)), мощностью множества выходных целевых связей СОout(t) и выходных ресурсных связей СRESout(t), а также соответствующими величинами суммарной проводимости WOout(t) и WRESout(t). Определяющим критерием влияния агента в МАС является его отношение к ресурсу.

УСЛОВИЯ ПОВЕДЕНИЯ АГЕНТОВ В МАС
В процессе обмена объем ресурса агента меняется. При уменьшении ресурса агента степень его влияния на МАС уменьшается. В предельном случае агент может поменять свой тип, например, превратиться из благонамеренного в альтруистичного. Напротив, при значительном увеличении своего влияния благонамеренный агент может стать эгоистичным. Отсюда можно выделить необходимые условия поведения агентов в МАС:
1) Res(ai(t)) > Resmin - условие индивидуального выживания агента;
2) Res(ai(t)) ≤ Resmax – условие социального поведения агента.

АССОЦИАЛЬНОЕ ПОВЕДЕНИЕ АГЕНТОВ В МАС
Если объем ресурса агента
Res(ai(t)) ≥ Resmax ,
(ситуация бесконтрольного возрастания его влияния), то это может привести к асоциальному поведению в МАС. Здесь предельным состоянием МАС будет являться ее распад, так как эгоистичный агент не сможет участвовать в обмене ресурсов из-за отсутствия участников обмена.
.