ЕГЭ ПО МАТЕМАТИКЕ2012 (часть 3)

С 3. Решите систему (1)
(2)
Решение: ОДЗ системы . Решим первое неравенство:
Для упрощения левой части неравенства понадобится равенство:
Его нетрудно доказать, если прологарифмировать обе части основания .
Итак, имеем неравенство:

Решим второе неравенство:
выполним замену
Сделаем обратную замену:
Осталось найти общую часть решений этих неравенств:
Ответ:

С 3. Решите систему: (1)
(2)
Решение: Решим первое неравенство. ОДЗ системы
Для решения первого неравенства немного по другому запишем первое слагаемое:
Так как обе части неравенства положительны, можно логарифмировать их по основанию 3, не меняя знака неравенства.

Итак, решение первого неравенства состоит из двух промежутков:
Решим второе неравенство:
Оно уже встречалось нам в предыдущем примере. Используем результат и получим:
Теперь найдем общую часть решения:
Ответ:

С 3. Решите систему: (1)
(2)
Решение: 1) ОДЗ системы неравенств определяется системой условий:
2) Решим первое неравенство системы

3) Решим второе неравенство:
(точка
выколота с учетом ОДЗ)
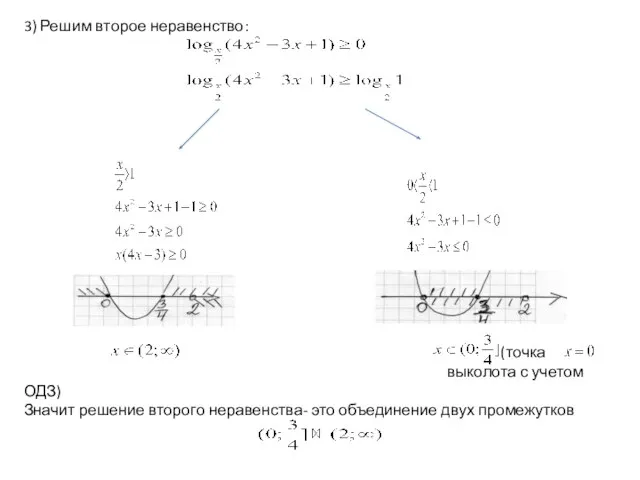
Значит решение второго неравенства- это объединение двух промежутков

4) Осталось найти общую часть решений:
Выясним расположение точки :
Ответ:

С 3. Решите систему:
Решение: Найдем ОДЗ:
Решим первое неравенство. Используем равенство:
Можно сделать замену:
Значит

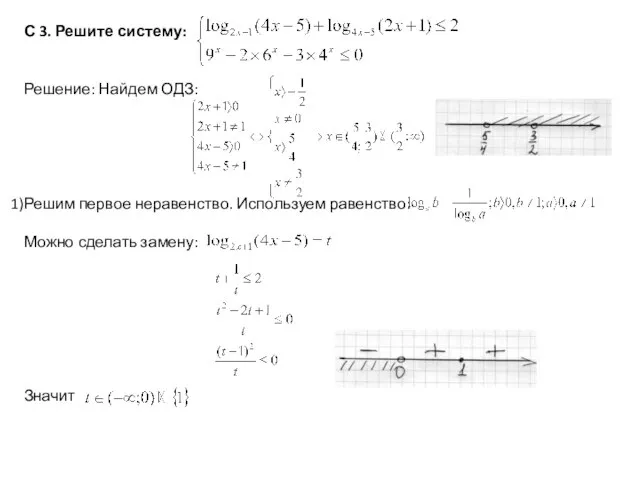
Выполняем обратную замену:
условие: условие:
Учитывая условие и ОДЗ Учитывая условие и ОДЗ- решения нет.
Получаем:

- удовлетворяет ОДЗ
Значит решением первого неравенства является множество
2) Решим второе неравенство:
однородное неравенство второй степени