Содержание
- 2. ОГЛАВЛЕНИЕ 21.1. Электрический колебательный контур. Собственные колебания. Формула Томсона. 21.2. Затухающие колебания. Вынужденные колебания в контуре.
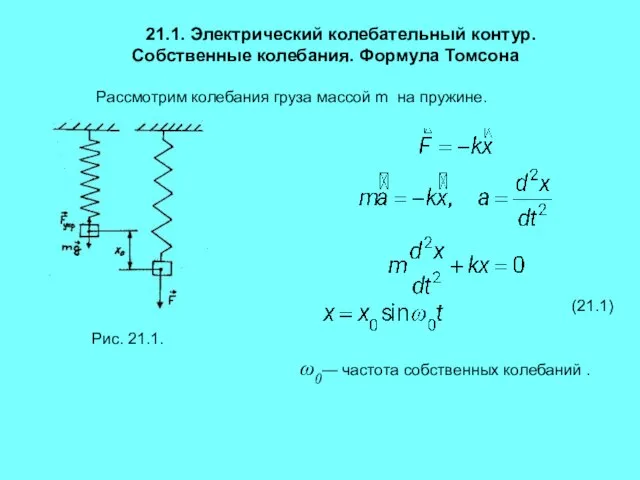
- 3. 21.1. Электрический колебательный контур. Собственные колебания. Формула Томсона Рассмотрим колебания груза массой m на пружине. Рис.
- 4. Процесс гармонического колебания
- 5. Рассмотрим колебания в колебательном контуре. Колебательным контуром называется цепь, составленная из катушки индуктивности и конденсатора. Рис.
- 6. Коэффициент 1/LC можно обозначить как ω2 где ω0 – частота собственных колебаний контура. Между током и
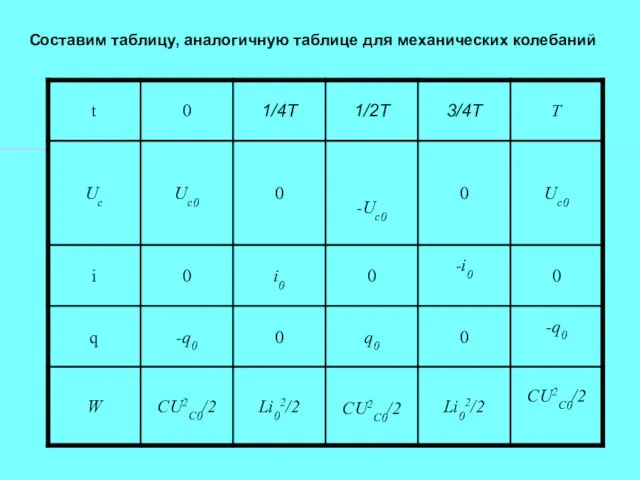
- 7. Составим таблицу, аналогичную таблице для механических колебаний
- 8. в цепи пойдет ток за счет запасенной энергии. Запас энергии будет уменьшаться, и ток будет слабеть.
- 9. 21.2. Затухающие колебания. Вынужденные колебания в контуре. Резонанс Рассмотренная ранее система является идеальной, т.к. в ней
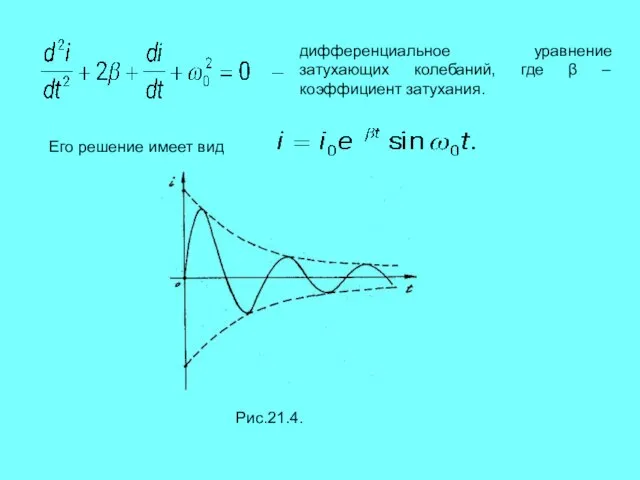
- 10. дифференциальное уравнение затухающих колебаний, где β – коэффициент затухания. Его решение имеет вид Рис.21.4.
- 11. Для поддержания незатухающих колебаний необходимо в колебательный контур включить внешний источник энергии, который будет осуществлять периодическую
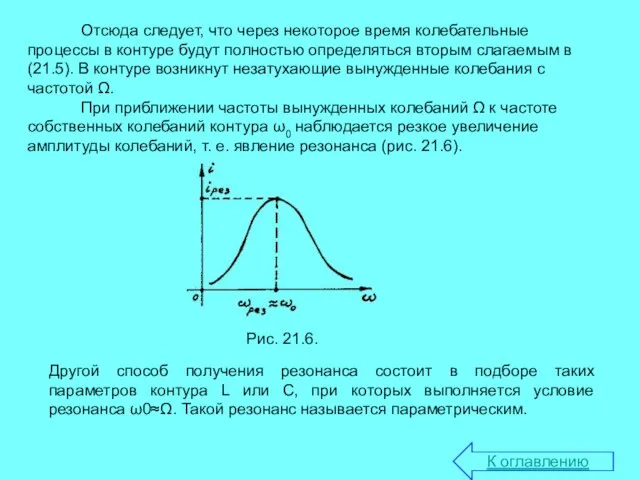
- 12. Отсюда следует, что через некоторое время колебательные процессы в контуре будут полностью определяться вторым слагаемым в
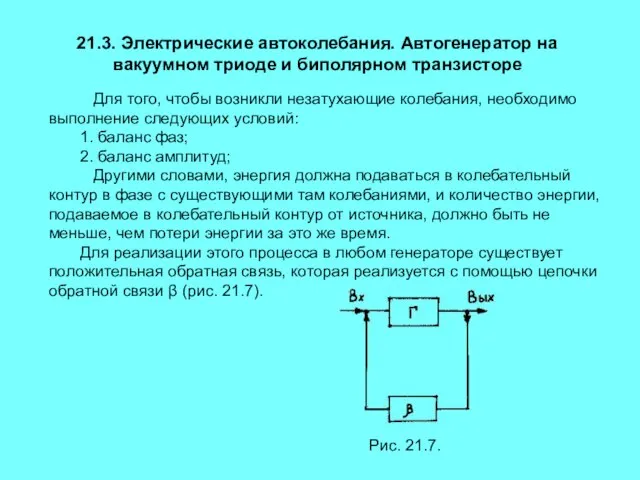
- 13. 21.3. Электрические автоколебания. Автогенератор на вакуумном триоде и биполярном транзисторе Для того, чтобы возникли незатухающие колебания,
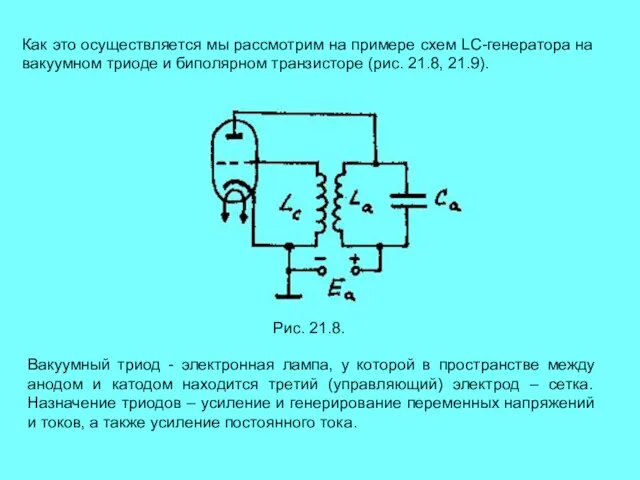
- 14. Как это осуществляется мы рассмотрим на примере схем LC-генератора на вакуумном триоде и биполярном транзисторе (рис.
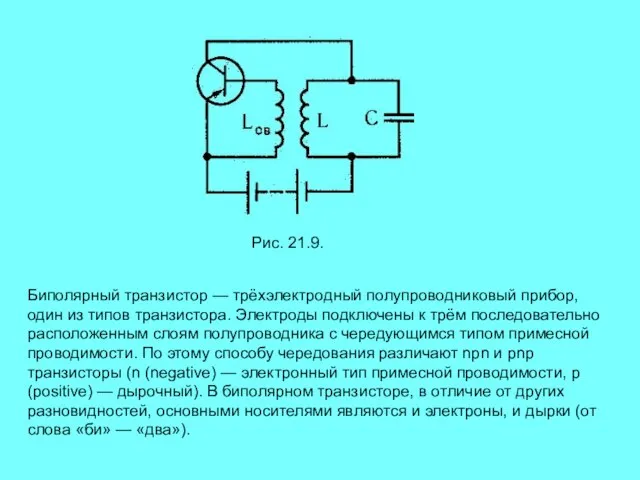
- 15. Рис. 21.9. Биполярный транзистор — трёхэлектродный полупроводниковый прибор, один из типов транзистора. Электроды подключены к трём
- 17. Скачать презентацию







 Презентация Microsoft PowerPoint
Презентация Microsoft PowerPoint Система стратегического планирования ООО «Сименс Россия»
Система стратегического планирования ООО «Сименс Россия» Презентация на тему Общая хирургическая инфекция
Презентация на тему Общая хирургическая инфекция  10 класс
10 класс Современные технологии и материалы
Современные технологии и материалы Почему нельзя жить без математики?
Почему нельзя жить без математики? Система Производственного менеджмента (СПМ)
Система Производственного менеджмента (СПМ) Моделирование из бумаги
Моделирование из бумаги Молочные и молокосодержащие продукты
Молочные и молокосодержащие продукты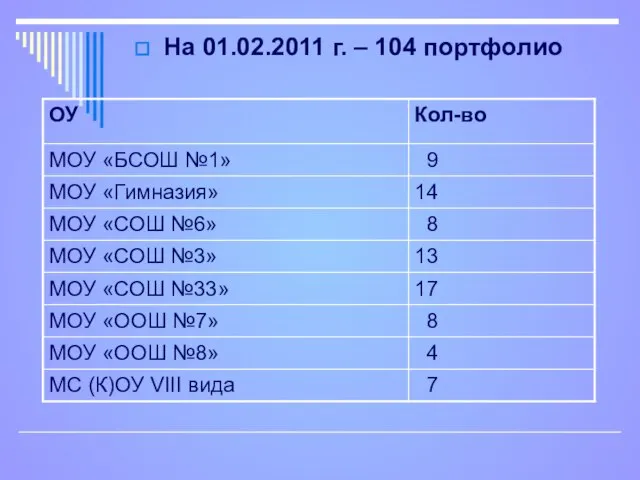 На 01.02.2011 г. – 104 портфолио
На 01.02.2011 г. – 104 портфолио Лихтенштейн
Лихтенштейн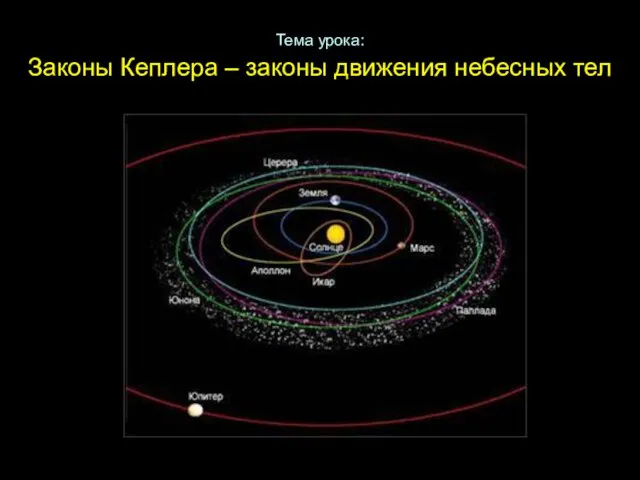 Тема урока: Законы Кеплера – законы движения небесных тел
Тема урока: Законы Кеплера – законы движения небесных тел Национальное пробуждение
Национальное пробуждение Мой класс и моя школа
Мой класс и моя школа Международный терроризм
Международный терроризм Культурные нормы. Мир человека
Культурные нормы. Мир человека Тела и вещества
Тела и вещества Юный разработчик. Занятие №9. Сборка. Динозавр
Юный разработчик. Занятие №9. Сборка. Динозавр Каталог Орифлейм. Акции
Каталог Орифлейм. Акции Моя семья Автор: Селиверстова Юлия, ученица 4-в класса
Моя семья Автор: Селиверстова Юлия, ученица 4-в класса «ПРАВА РЕБЁНКА»
«ПРАВА РЕБЁНКА» Media of the Usa
Media of the Usa Свойства льняных и хлопчатых тканей
Свойства льняных и хлопчатых тканей Рисуем трамвай
Рисуем трамвай Фарфор и керамика
Фарфор и керамика Солярис
Солярис Безопасность на транспорте
Безопасность на транспорте Атом мирный и военный
Атом мирный и военный