Элементы теории графов

Содержание
1. Основные понятия теории графов
2. Степень вершины
Введение
5. Ориентированные графы
6. Изоморфизм графов
7. Плоские графы
8. Операции над графами
9. Способы задания графов
3. Маршруты, цепи, циклы
10. Некоторые типы графов

ВВЕДЕНИЕ
Теория графов в качестве дисциплины может рассматриваться как раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами (изучение объектов).
Как прикладная дисциплина теория графов позволяет описывать и исследовать многие технические, экономические, биологические и социальные системы.
Особенно широкое применение теории графов в таких областях прикладной математики, как программирование, теория конечных автоматов, в решении вероятностных и комбинаторных задач.

1. Основные понятия теории графов
Число вершин графа G обозначим р, а число ребер – q
Граф называется полным, если каждые две различные вершины его соединены одним и только одним ребром.

Степенью вершины называется число ребер графа, которым принадлежит эта вершина. Еще называют его валентностью и обозначают d(v), deg(v). Вершина графа, для которой d(v)=0, является изолированной, если d(v)=1, то висячей.
Deg(6)=3, deg(5)=1, 5 – висячая вершина
N(3)={2,1,6,4}, deg(7)=0, 7 – изолированная вершина
Вершина называется нечетной, если d(v) – нечетное число, четной если d(v) – четное число. Степень каждой вершины полного графа на единицу меньше числа его вершин.
Рис 2.1
2. Степень вершины

В графе G(V,E) сумма степеней всех его вершин – число четное, равное удвоенному числу ребер графа.
Число нечетных вершин любого графа четно.
Во всяком графе с n вершинами, где n ≥ 2 всегда найдутся, по меньшей мере, две вершины с одинаковыми степенями.
Если в графе с n вершинами (n ≥ 2) в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени 0, либо в точности одна вершина степени n-1.
Свойства степени вершины

Маршрутом в графе называется чередующаяся последовательность вершин и ребер, в которой любые два соседних элемента инцидентны:
Если то маршрут замкнут, в противном случае открыт.
Если все ребра различны, то маршрут называется цепью.
Если все вершины различны, то маршрут называется простой цепью. В цепи вершины называются концами цепи, т. е. цепь концами соединяет вершины . Цепь, соединяющая вершины , обозначается ( ). Очевидно, что если есть цепь, соединяющая вершины - простая цепь, соединяющая эти вершины.
Замкнутая цепь называется циклом, замкнутая простая – простым циклом, число циклов обозначается z(G). Граф без циклов – ациклический.
Длинной маршрута называется количество ребер в нем (с повторениями).
Если маршрут , то длина маршрута М равна k, обозначается
3. Маршруты, цепи, циклы

Две вершины графа называются связными, если существует соединяющая их простая цепь. В противном случае две вершины называются не связными.
Граф называется связным, если каждые две вершины связные.
Граф называется несвязным, если хотя бы две его вершины несвязные.
Так, на рисунке любая пара вершин, взятая из набора А,Б,В,Г,Д ,будет связной, т.к. от любой из них к любой можно "пройти" по ребрам графа.
Рис 4.2
Рис 4.1
4. Связность графов

Если элементы множества Е графа G(V, E) – упорядоченные пары, то граф называется ориентированным или орграфом.
Ребро графа называется ориентированным, если одну вершину ребра считают началом ребра а другую концом, на рисунке изображают стрелкой между вершинами. Граф у которого все ребра ориентированы – ориентированный.
Ориентированное ребро
Неориентированное ребро
Одна и та же вершина ориентированного графа может служить началом для одних ребер и концом для других, поэтому различают две степени вершины:
Степенью выхода вершины орграфа – число выходящих из вершины ребер;
Степенью входа вершины орграфа – число входящих в вершину ребер.
Рис 5.1
Рис 5.2
5. Ориентированные графы

В орграфах в зависимости от сочетания степеней входа и выхода для данной вершины рассматриваются три случая:
Изолированной вершиной называется вершина у которой степень входа и степень выхода равны 0;
Источником называется вершина, степень выхода которой положительна, а степень входа равна 0;
Стоком называется вершина, степень входа которой положительна, а степень выхода равна 0.
Путем в ориентированном графе называется последовательность ориентированных ребер.
Простым путем в ориентированном графе называется путь, в котором ни одна вершина не содержится более одного раза (Рис 5.3). На рис 5.4 изображен не простой путь.
Рис 5.3
Рис 5.4

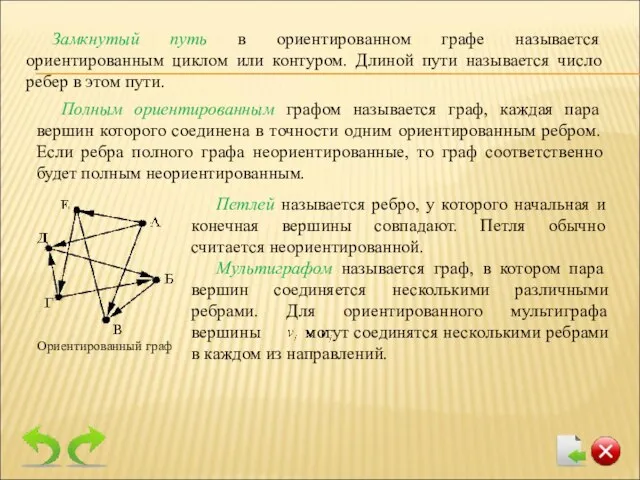
Петлей называется ребро, у которого начальная и конечная вершины совпадают. Петля обычно считается неориентированной.
Мультиграфом называется граф, в котором пара вершин соединяется несколькими различными ребрами. Для ориентированного мультиграфа вершины могут соединятся несколькими ребрами в каждом из направлений.
Замкнутый путь в ориентированном графе называется ориентированным циклом или контуром. Длиной пути называется число ребер в этом пути.
Полным ориентированным графом называется граф, каждая пара вершин которого соединена в точности одним ориентированным ребром. Если ребра полного графа неориентированные, то граф соответственно будет полным неориентированным.
Ориентированный граф

Если ребра графа ориентированы, то их направление в изоморфных графах должно совпадать. Изоморфизм есть отношение эквивалентности, так как обладает свойствами рефлексивности, симметричности, транзитивности. Для того чтобы граф был изоморфен графу , необходима такая подстановка, которая бы установила взаимно-однозначное соответствие между вершинами графа и их ребрами.
При замене графа любым ему изоморфным все свойства графа сохраняются. Строго говоря, графы, отличающиеся только нумерацией вершин, являются изоморфными.
6. Изоморфизм графов
Два графа называются изоморфными, если между множествами их вершин существует биективное (взаимно-однозначное) соответствие, такое, что вершины соединены ребрами в одном из графов в том и только в том случае, когда соответствующие им вершины соединены в другом графе.

Пример «Изоморфизма графов»

7. Плоские графы
В качестве характеристики плоского представления графа вводится понятие грани (рис 7.1). Грань в плоском представлении графа называется часть плоскости, ограниченная простым циклом и не содержащая внутри других циклов.
Рис 7.1

8. Операции над графами

9. Способы задания графов
Аналитический способ задания графов
Граф G(V,E) задан, если задано множество элементов V и отображение Е множества V в V. Отображение Е может быть как однозначным, так и многозначным. В общем случае на V и E никаких ограничений не накладывается.

10. Некоторые типы графов
Эйлеровы графы
Эйлеровым путем в графе называется путь, содержащий все ребра графа.
Эйлеровым циклом или эйлеровой цепью называется цикл, содержащий все ребра графа и притом по одному разу. Граф, обладающий эйлеровым циклом, называется эйлеровым графом.
Замкнутую линию, если ее можно начертить, не отрывая карандаша от бумаги, проходя при этом каждый участок в точности один раз, принято называть уникурсальной. Рисунок графа, обладающего эйлеровым путем или циклом, является уникурсальной линией.
Теорема 1. Если граф G(V,E) обладает эйлеровым циклом, то он связный и все его вершины четные.
Теорема 2. Если граф G(V,E) связный и все его вершины четные, то он обладает эйлеровым циклом.

Гамильтоновы графы
Граф, обладающий гамильтоновым циклом, называется гамильтоновым графом. Гамильтоновым циклом, называется цикл, или путь, проходящий через каждую вершину графа в точности по одному разу.
Эйлеровы и гамильтоновы пути сходны по способу задания. Первые содержат все ребра, и притом по одному разу, вторые – все вершины по одному разу. Для решения вопроса о существовании эйлерова цикла в графе достаточно выяснить, все ли его вершины четные.
Условия существования гамильтоновых циклов
Всякий полный граф является гамильтоновым, так как содержит простой цикл, которому принадлежат все вершины данного графа.
Если граф, помимо простого цикла, проходящего через все его вершины, содержит и другие ребра, то он также является гамильтоновым.
Если граф имеет один гамильтонов цикл, то он может иметь и другие гамильтоновы циклы.