Элементы теории вероятностей

План лекции
Случайное событие. Вероятность события.
Теоремы сложения и умножения вероятностей.
Формула полной вероятности. Формула Байеса.

Понятие случайного события
События (явления) подразделяют на три вида:
достоверные,
невозможные,
случайные.

Достоверное событие
событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий.
Примером достоверных событий может быть и наступление времени 15.00 после 14.59, и образование кристаллов солей после испарения соленой воды и др.

Невозможное событие
событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий.
В качестве невозможных событий можно назвать и образование устойчивого следа в воздухе после полета птицы, и самопроизвольное преобразование гранита в воду, и притяжение магнитом полиэтилена и др.

Случайное событие
событие, которое при осуществлении совокупности условий может либо произойти, либо не произойти.
Примерами случайных событий являются выбор конкретной конфеты из коробки, содержащей одинаковые конфеты, перемещение броуновской частицы, бросание монетки с целью получить на верхней стороне “орел” или “решка” и т.д.

Несовместные события
если появление одного из них исключает появление других событий в одном и том же испытании.
В качестве примера несовместных событий укажем розыгрыш в лотерею, где событие выигрыша всегда несовместно с проигрышем.

Независимые события
если появление одного события не изменяет вероятности другого события.
В качестве примера независимых событий укажем бросание подряд 2 монеток с целью получить на верхней стороне “орел” или “решка”.

Полная группа событий
Несколько случайных несовместных событий образуют полную группу, если в результате испытания появится только одно из них.
Примером полной группы - выбор случайной цифры в забытом телефонном номере, который состоит из 10 несовместных событий - десятичных цифр 0, 1, 2, 3 … 9.

Если полная группа состоит только из двух событий, то такие события обычно называют противоположными и обозначают A - исходное событие, А противоположное.
Противоположные события
Например, стрелок выстрелил по мишени. Обязательно произойдет одно из двух событий: попадание, промах.

Классическое определение вероятности события
Вероятностью события A называют отношение числа благоприятствующих этому событию элементарных событий к общему числу всех равновозможных несовместных элементарных событий, образующих полную группу.
где m- число элементарных событий, благоприятствующих событию A,
n- число всех возможных элементарных событий.

Числовые значения вероятностей
вероятность достоверного события равна P(A)=n/n=1.
вероятность невозможного события равна P(A)=0/n=0.
вероятность случайного события заключена в пределах 0

Комбинаторика
раздел математики, изучающий количество комбинаций, которые можно составить из элементов, заданного конечного множества.
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения.
Pn = n!,
где n! = 1⋅2⋅3…n. Читается как “n факториал”. Заметим, что 0!=1.

Комбинаторика
Размещениями называют комбинации, составленные из n различных элементов по m элементов в каждом, которые отличаются либо элементами, либо их порядком.

Комбинаторика
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов в каждом, которые отличаются хотя бы одним элементом. При подсчете числа сочетаний порядок элементов не важен.

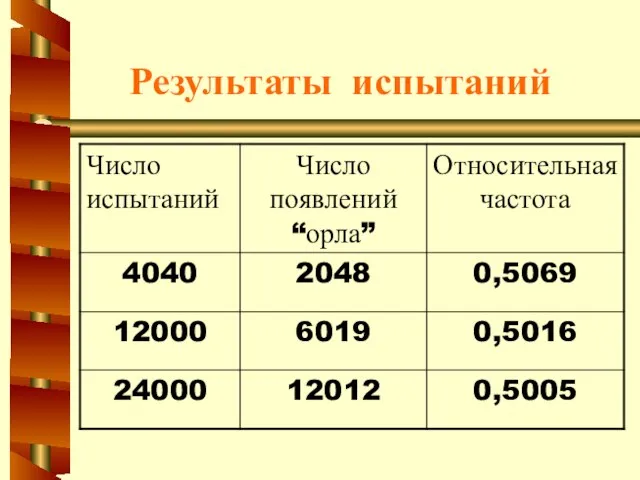
Относительная частота события A
отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.
m - число испытаний, где проявилось событие A,
n - число всех испытаний.

Статистическое определение вероятности события
Вероятностью события A называют число, к которому стремиться относительная частота события A при увеличении количества испытаний.

Результаты испытаний

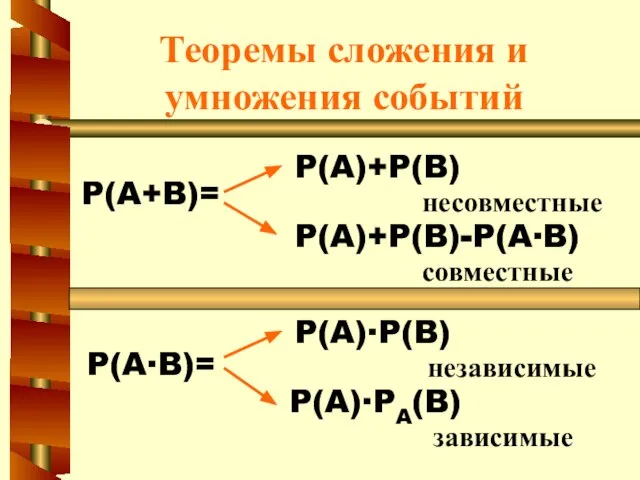
Теоремы сложения и умножения событий
P(A+B)=
P(A∙B)=
P(A)+P(B)
P(A)+P(B)-P(A∙B)
P(A)∙P(B)
P(A)∙PA(B)
несовместные
совместные
независимые
зависимые

Теорема сложения несовместных событий
Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
P(A+B)=P(A)+P(B)

Теорема сложения совместных событий
Вероятность появления одного из двух совместных событий, безразлично какого, равна сумме вероятностей этих событий минус вероятность их совместного появления:
P(A+B)=P(A)+P(B)-P(A∙B)

Теорема умножения независимых событий
Вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий:
P(A∙B)=P(A) ∙ P(B)

Теорема умножения независимых событий (пример)
Найти вероятность совместного появления “орла” при одном бросании двух монет.
Решение. Вероятность появления “орла” для первой монеты P(A)=0,5.
Вероятность появления “орла” для второй монеты P(B)=0,5. Так как события A и B независимые, то:
P(A·B)=P(A) · P(B)=0,5 · 0,5=0,25.

Теорема умножения зависимых событий
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого события, вычисленную в предположении, что первое событие уже произошло:
P(A∙B)=P(A) ∙ PA(B)

Условная вероятность PA(B)
вероятность события B, вычисленную в предположении, что событие A уже наступило.

Теорема умножения зависимых событий (пример)
В коробке имеется две израсходованные и восемь новых ампул. Найдите вероятность того, что подряд будут взяты одна новая и одна израсходованная ампула.
Решение. Вероятность события A (извлечь новую ампулу) равна P(A)=8/10=0,8.
Вероятность события B (извлечь пустую ампулу после извлечения новой) равна PA(B)=2/9≈0,222.
Искомая вероятность
P(A · B)=P(A) · PA(B) = 0,8·0,222 ≈ 0,178.

Формула полной вероятности
Вероятность события A, которое может наступить лишь при условии появления одного из несовместных событий B1, B2 , B3, … , Bn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события A:
P(A)=P(B1)PB1(A)+
P(B2)PB2(A)+… +P(Bn)PBn(A)

Формула полной вероятности
P(A)=P(B1)PB1(A)+
P(B2)PB2(A)+… +P(Bn)PBn(A)
краткая запись

Формула полной вероятности (пример)
В первой коробке лежит 20 пар операционных резиновых перчаток из них 15 неповрежденных, а во второй коробке – 10 пар перчаток из них 9 неповрежденных. Найти вероятность того, что взятая наудачу пара перчаток неповрежденная (из любой наудачу выбранной коробки)?

Формула полной вероятности (пример)
Обозначим через A событие “извлеченная пара неповрежденная”.
Вероятность того, что пара перчаток извлечена
из первой коробки P(B1)=1/2,
из второй коробки - P(B2)=1/2.
Условная вероятность того, что из первой коробки извлечена неповрежденная пара равна PB1(A)=15/20=0,75, из второй коробки - PB2(A)=0,9.
P(A)=P(B1)PB1(A)+P(B2)PB2(A)=
=0,5·0,75+0,5·0,9=0,82

Формула Байеса
(переоценки вероятности)
Пусть событие A может наступить лишь при условии появления одного из несовместных событий B1, B2 , B3, … , Bn ,образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Произведено испытание, в результате которого появилось событие A. Как же изменились вероятности гипотез (в связи с тем, что событие A уже наступило)?

Формула Байеса
i=1,2,…, n

Формула Байеса (пример)
Ампулы, изготовляемые цехом фармацевтического завода, попадают для проверки их на стандартность к одному из двух контролеров.
Вероятность того, что ампула попадает к первому контролеру, равна 0,6, а ко второму – 0,4. Вероятность того, что годная ампула будет признана стандартной первым контролером, равна 0,94, а вторым – 0,98. Годная ампула при проверке была признана стандартной.
Найти вероятность того, что эту ампулу проверил первый контролер.

Формула Байеса (пример)
Решение
Обозначим через A событие, состоящее в том, что годная ампула признана стандартной.
Можно сделать два предположения:
ампулу проверил первый контролер (гипотеза B1);
ампулу проверил второй контролер (гипотеза B2).
PA(B1)=(0,60·0,94)/( 0,60 · 0,94+0,4 · 0,98) ≈ 0,59.

Формула Бернулли
Вероятность одного события B, состоящего в том, что в n независимых испытаниях событие A наступит k раз и не наступит n-k раз, по теореме умножения вероятностей независимых событий равна pk(1-p)n-k.
Но таких событий B может быть столько, сколько существует вариантов выбора k элементов из n ( или число сочетаний) .
q=1-p

Формула Бернулли (пример)
Требуется узнать какова вероятность выпадения “орла” ровно 4 раза при подбрасывании монеты 6 раз?
Решение.
Считаем каждое подбрасывание монеты независимым. Очевидно, что p=0,5, а q=0,5:

Литература
1. Ремизов А.Н. Медицинская и биологическая физика. -М.: Дрофа, 2007.- С. 26-31.
2. Шаповалов К.А. Основы высшей математики. - Красноярск: ООО Печатные технологии , 2004.- С. 62-89.