Евклидово физическое пространство, циклическое время и универсальность взаимодействий

Пространство Минковского или…?
Геометрия М. – основная структура физического пространства-времени (ПВ)
В настоящее время рассматривается как «скелет» реалистической структуры ПВ – многомерного, искривленного, с нетривиальной топологией, дискретного (?), квантованного (?) и др.
Однако истинная размерность и структура ПВ по-прежнему неясна, как неясен и ответ на старый вопрос: почему «видимое» физ. пространство трехмерно? Плюс Время??
Геометрия М. – математически ничем не выделена, не следует из общих принципов. В частности, не известна алгебраическая структура, порождающая эту геометрию. Тем более неоднозначны расширения М.
С общефиз.точки зрения геометрия М. имеет ряд замечательных свойств (причинность, универсальная скорость взаимодействий), однако и сущ. недостатки (нет взаимной синхронизации (!), глобального параметра эволюции, отсутствуют фазовые отношения, нет временной необратимости и пр.)

О выделенности евлидовых геометрий
С общематематической т. зрения, выделенным является не только 3-мерное евклидово пространство Е3, но и Е4.
Действительно, исключительная (1+3) алгебра кватернионов Гамильтона Q имеет группу симметрии по умножению SO(3), по норме – SO(4).
Криволинейные расширения Е3,4 – римановы 3- и 4- многообразия – также исключительны (сфера Перельмана-Пуанкаре S3, множественные. дифференциальные структуры Дональдсона на 4D топологически эквивалентных многообразиях и др.)
В квантовой теории поля Е4 также выделено (самодуальные структуры типа инстантонов, удобство функционального интегрирования и пр.), однако не рассматриваются как отвечающие истинной физической геометрии (главный недостаток – нет причинности – структуры светового конуса).

Евклидово пространство-время?
Тем не менее, ряд подходов последнего времени кладет в основу физической геометрии именно евклидово пространство 4-х или 6-ти измерений.
Упомянем вначале теорию «поля времени» А.Б. Пестова (A.B. Pestov), связывающего ход физического времени с «потоком геодезических» на 4D римановом многообразии. Лоренцева структура вводится через векторные поля с различной киральностью.
За рубежом возрастает интерес к т.н. подходу «proper time physics» (G.Montanus) или к «Euclidean Relativity» (Montanus, Almeida et al.), см., например, сайт www.euclideanrelativity.com
Основная идея – предположение (восходящее к Ф.Клейну, Ю.Румеру, Р.О.ди Бартини и др.) о движении всех частиц в расширенном пространстве с единственной и универсальной скоростью – «скоростью света». Ниже – подробнее.

«Евклидова относительность» Г. Монтануса
Основу стандартной СТО составляет формула интервала Минковского
Величина ds/c – промежуток «собственного времени» частицы, математически – не полный дифференциал, а метрика «псевдоевклидова пространства» М
Тривиально перепишем предыдущую формулу в виде
и будем рассматривать ds как 4-ю «внутреннюю» координату, а dt – как промежуток «абсолютного», глобального, квазиньютоновского времени, который по основному предположению, одинаков для всех частиц материи.
Т.о., время в данной парадигме определяется суммарным и универсальным перемещением материальных образований в расширенном 4D евклидовом пространстве. (Аналогия с подходом В.В. Аристова, реляционной статистической теорией) Эквивалентно: существует единственная скорость движения всех частиц в расширенном пространстве – «скорость света».

Для всех частиц в покое (v1= v2= v3=0)→ v0=c, “внутреннее движение”, задает «ход собственного времени»; обратно, «фотон» не движется в 4-м измерении.
Движущуюся частицу следует получать из неподвижной с помощью евклидова поворота в 0-1, 0-2, 0-3 плоскостях, например
так что «темп хода времени» замедляется в полном соответствии со СТО. Наглядное объяснение парадокса близнецов и пр.!
С другой стороны, статус 4-й координаты, ее выделенность остаются непонятными (как и статус дополнит. координат в теориях Калуцы-Клейна).

6D геометрия Урусовского
И.А. Урусовский в серии работ 1996-2011 гг. предложил и разработал «новую 6-мерную трактовку СТО» и гравитации. Исходные предположения – это
1) универсальная скорость всех материальных образований в расширенном (3+3) мерном пространстве и
2) их периодическое регулярное движение по окружности (комптоновского радиуса ) в дополнительном подпространстве – гипотеза «внутренних часов электрона» или «циклического (фазового) времени» (Л.де Бройль, Zitterbewegung Э.Шредингера и др.).
Собственное время частицы пропорционально числу оборотов (изменению фазы) при вращении в дополнит. подпространстве. Наличие 3-х доп. координат позволяет естественно описать спин и изоспин частицы как проекцию момента количества движения на основное и дополнительное подпространства соответственно.
По существу все основные соотношения СТО, в том числе и динамические, следуют из Ньютоновской физики в 6-мерии!

Итак, имеем «два времени» (Спасков А.Н,): 1) «трансляционное», линейное, выступающее как параметр эволюции и связанное с перемещениями в полном пр-ве, абсолютное (?), глобальное (?), и
2) «циклическое», фазовое, характеризующее относительную быстроту «внутренних процессов», относительное (?), локальное (?).
На самом деле, у Урусовского интерпретация (неявно) другая, не Монтануса и пр., а ближе к Эйнштейну («6D трактовка СТО»):величина ds и изменение фазы dφ инвариантны (число оборотов = inv !?). С другой стороны, ds здесь не метрика!!?
Оказывается, возможны обе трактовки: существуют две группы преобразований симметрии основного соотношения для приращений и, соответственно, для 3-сферы скоростей:

Первая группа – 6-параметрич. евклидова группа SO(4) вращений 3-сферы, dt – метрика, абсолютное инвариантное глобальное время; ds – замедляется, не инвариантно.
Вторая группа – обычная группа Лоренца, инвариант ds (но не универсально!), dt – не инвариантно, относительное локальное время (но не координата!), результат -- прежняя «светоподобная» конфигурация, но «в другом времени»!
На сфере скоростей группа Лоренца действует нелинейно, по аналогии с канонич. формулой сложения скоростей. Т.о., имеем реализацию лоренцевой динамики на сфере S3 (по аналогии с известной реализацией Пенроуза лоренцевой динамики на S2)!!

В качестве примера релятивистских соотношений в 6D имеем универсальную связь энергии с импульсом (одинаковую для массивных частиц и фотонов!):
Среди результатов, полученных Урусовским в рамках 6D подхода, следует отметить еще 1) спектр атома водорода с учетом тонкой структуры, 2) кварковую модель нуклонов, 3) новую трактовку гравитации (как проекции космологической силы, удерживающей частицы в окрестности R3), 4) новую трактовку расширения Вселенной (объясняющая многие парадоксы стандартной космологии) и т.п.
С фундаментальной точки зрения, важно, что подход Урусовского позволяет связать геометрию ПВ с фазовыми соотношениями (открывая этим путь к геометризации квантовой теории), а также прямо выводит универсальную кинематику частиц (и, в какой-то степени, их динамику) из чистой геометрии!
Недостаточность: 1) не видно общего обоснования исходных постулатов, 2) не решается проблема спектра масс, 3) не ясна структура и кинематика фотонов и пр. → БОЛЕЕ ОБЩИЙ ПОДХОД!?

Основные положения алгебродинамики
В алгебродинамике (В.К) постулируется существ исключит. по внутр.св-вам алгебры пространства -времени
Алгебра ПВ полностью определяет как геометрию ПВ (через группу автоморфизмов → группу движений), так и динамику полей-частиц (через условия аналитичности функций → уравнения поля и особенности полей-функций → частицы)
В качестве алгебры ПВ рассматривается алгебра комплексных кватернионов (бикватернионов) В = алгебре 2Х2 матриц с комплексными элементами.
Условия В-аналитичности – обобщ ур-ния Коши-Римана (ОУКР) – оказ-ся нелинейными – теория взаимодействующих полей.
Следствия ОУКР: присутствие калибровочной и спинорной (твисторной) структуры, тождественное выполнение уравнений Максвелла, «автоквантование» электрического заряда и пр.
Геометрия, индуцир. алгеброй В – комплексно 4D (вещественно 8D)→обрезается «руками» до М - теория лоренц-инвариантна.
Новая концепция времени как параметра эволюции, связанного с локальным сохранением первичного поля (имеющего бикватернионно-спинорно-твисторную природу).
Локальная эволюция –светоподобный перенос первичного поля – концепция Потока Предсвета = Поток Времени
Частицы (геометрически) – каустики предветового потока – вся материя имеет светоподобную природу!

Естественная комплексная В-геометрия ПВ
Не существует алгебры, индуцирующей геометрию Минковск. М
С др. стороны, М не содержит фазовой компоненты. При этом 4С=8R комплексная геометрия алгебры В естественно факторизуется на макрогеометрию (определяемую модулями комплексных координат) и микрогеометрию «слоя», связанную с их фазами (В.К., 2005). Макрогеометрия оказывается изоморфной М, однако при этом билинейной по координатам первичного комплексного В-пространства Zμ
При этом, однако, связь между фазовой и трансляционной кинематикой отсутствует. Поэтому предложенную ранее вещественную геометрию, индуцированную В, следует рассматривать как динамическую (связанную с энергией-импульсом материальных образований).
Собственно геометрия (расширенного) ПВ оказывается сложнее и напоминает геометрию Урусовского. Тесно связана с кинематикой в первичном комплексном В-пространстве. Такая кинематика невозможна в пространстве Минковского и приводит к ряду неожиданных свойств физической картины Мира.

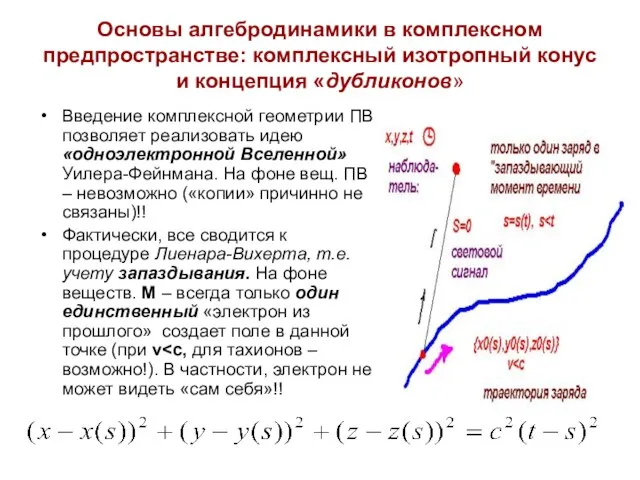
Основы алгебродинамики в комплексном предпространстве: комплексный изотропный конус и концепция «дубликонов»
Введение комплексной геометрии ПВ позволяет реализовать идею «одноэлектронной Вселенной» Уилера-Фейнмана. На фоне вещ. ПВ – невозможно («копии» причинно не связаны)!!
Фактически, все сводится к процедуре Лиенара-Вихерта, т.е. учету запаздывания. На фоне веществ. М – всегда только один единственный «электрон из прошлого» создает поле в данной точке (при v

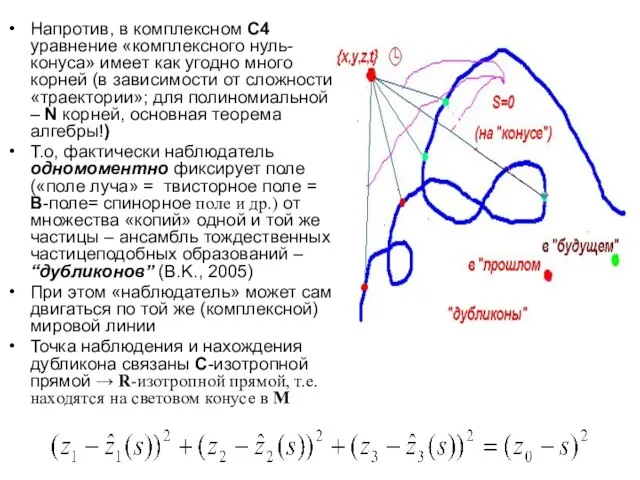
Напротив, в комплексном С4 уравнение «комплексного нуль- конуса» имеет как угодно много корней (в зависимости от сложности «траектории»; для полиномиальной – N корней, основная теорема алгебры!)
Т.о, фактически наблюдатель одномоментно фиксирует поле («поле луча» = твисторное поле = В-поле= спинорное поле и др.) от множества «копий» одной и той же частицы – ансамбль тождественных частицеподобных образований – “дубликонов” (В.K., 2005)
При этом «наблюдатель» может сам двигаться по той же (комплексной) мировой линии
Точка наблюдения и нахождения дубликона связаны С-изотропной прямой → R-изотропной прямой, т.е. находятся на световом конусе в М

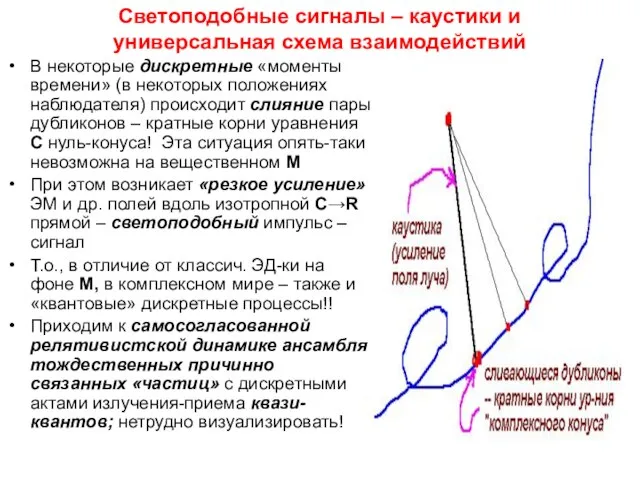
Светоподобные сигналы – каустики и универсальная схема взаимодействий
В некоторые дискретные «моменты времени» (в некоторых положениях наблюдателя) происходит слияние пары дубликонов – кратные корни уравнения С нуль-конуса! Эта ситуация опять-таки невозможна на вещественном М
При этом возникает «резкое усиление» ЭМ и др. полей вдоль изотропной С→R прямой – светоподобный импульс – сигнал
Т.о., в отличие от классич. ЭД-ки на фоне М, в комплексном мире – также и «квантовые» дискретные процессы!!
Приходим к самосогласованной релятивистской динамике ансамбля тождественных причинно связанных «частиц» с дискретными актами излучения-приема квази-квантов; нетрудно визуализировать!

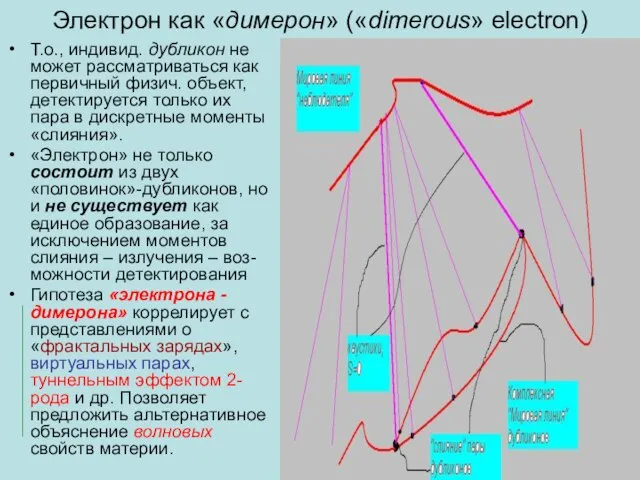
Электрон как «димерон» («dimerous» electron)
Т.о., индивид. дубликон не может рассматриваться как первичный физич. объект, детектируется только их пара в дискретные моменты «слияния».
«Электрон» не только состоит из двух «половинок»-дубликонов, но и не существует как единое образование, за исключением моментов слияния – излучения – воз- можности детектирования
Гипотеза «электрона - димерона» коррелирует с представлениями о «фрактальных зарядах», виртуальных парах, туннельным эффектом 2-рода и др. Позволяет предложить альтернативное объяснение волновых свойств материи.

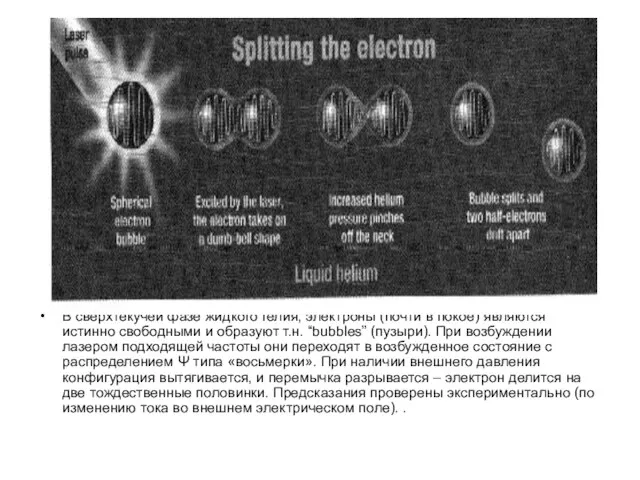
В сверхтекучей фазе жидкого гелия, электроны (почти в покое) являются истинно свободными и образуют т.н. “bubbles” (пузыри). При возбуждении лазером подходящей частоты они переходят в возбужденное состояние с распределением Ψ типа «восьмерки». При наличии внешнего давления конфигурация вытягивается, и перемычка разрывается – электрон делится на две тождественные половинки. Предсказания проверены экспериментально (по изменению тока во внешнем электрическом поле). .

Комплексная геометрия как геометрия расширенного ПВ
Аналогично М, первичное поле + структура каустик сохраняются вдоль изотропных комплексных (С) прямых – образующих С нуль-конуса. Уравнение для его элемента имеет вид
Представляя Zμ как сумму Re и Im частей, имеем две квадрики в R6, задающие два 4-мерных и взаимно ортогональных евклидовых (под)пространства X и Y приращений-скоростей (топологии S3xS3)
причем в каждом из них движение происходит с универсальной скоростью «света» с. Эта геометрия допускает конфигурации типа Монтануса-Урусовского: так, частица, покоящаяся в (3D) X-подпростр.→ движется со скоростью света в (3D) Y-подпространстве
При дополнит. условии имеем
в точности конфигурацию Урусовского вращающейся частицы (радиус вращения R, как и у него, неквантован?! Есть соображения! ). Возможны более общие конфигурации, напр., вращение по сфере S2.

Фаза «внутреннего вращения» и квантовая интерференция
Для конфигураций Урусовского «набег фазы» вдоль траектории автомат. пропорционален приращению собственного времени. Совместно с предположением об «электроне-димероне» это ведет к возможности чисто классического объяснения квантовой интерференции.

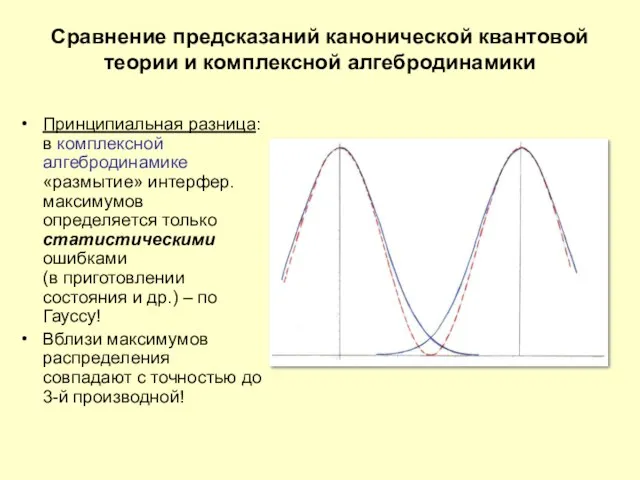
Сравнение предсказаний канонической квантовой теории и комплексной алгебродинамики
Принципиальная разница: в комплексной алгебродинамике «размытие» интерфер. максимумов определяется только статистическими ошибками (в приготовлении состояния и др.) – по Гауссу!
Вблизи максимумов распределения совпадают с точностью до 3-й производной!