s neurčitosťou
Jednotlivé kombinačné funkcie môžu byť definované rôzne. Intuitívne možno stanoviť ich interpretáciu.
PP S NEURČITOSŤOU môžeme interpretovať:
AK je predpoklad úplne splnený, POTOM záver platí s váhou w.
AK predpoklad nie je splnený úplne, POTOM príspevok pravidla k posilneniu dôvery v záver je menší ako w.
PRI PARALELNEJ KOMBINÁCII:
AK prvé aj druhé pravidlo podporuje(oslabuje) záver POTOM výsledná váha je posilňovaná(oslabovaná).
AK jedno pravidlo záver podporuje a druhé ho vyvracia POTOM sa vplyvy eliminujú


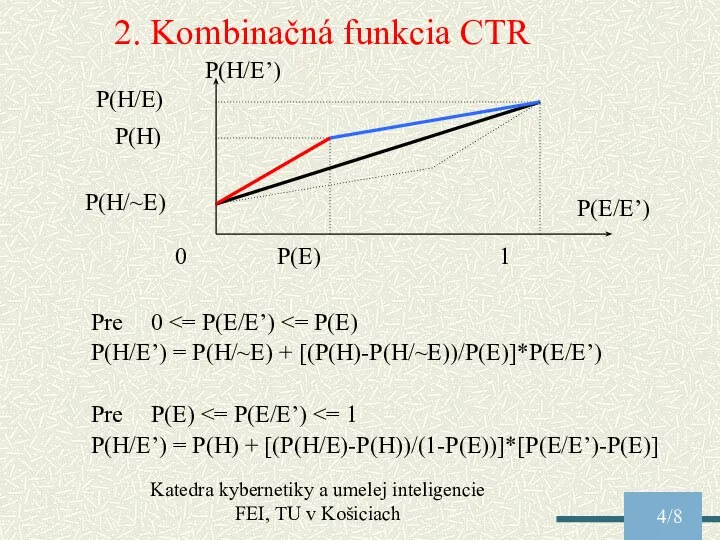


 Действия с десятичными дробями
Действия с десятичными дробями Стороны горизонта. Ориентирование
Стороны горизонта. Ориентирование Репозиторий БГПУ
Репозиторий БГПУ Презентация на тему Своя игра по астрономии
Презентация на тему Своя игра по астрономии  Обучение ведению мяча на месте и в движении
Обучение ведению мяча на месте и в движении Тема учебного проекта:Русская лексика с точки зрения сферы ее употребления
Тема учебного проекта:Русская лексика с точки зрения сферы ее употребления Всесезонная ярмарка
Всесезонная ярмарка Природные стихии в народном творчестве
Природные стихии в народном творчестве Сокращение потерь филиала за счет минимизирования краж
Сокращение потерь филиала за счет минимизирования краж Световой дизайн интерьера
Световой дизайн интерьера Признаки равенства треугольников
Признаки равенства треугольников Презентация на тему Бокс
Презентация на тему Бокс Русский народный костюм
Русский народный костюм Города-герои великой отечественной войны
Города-герои великой отечественной войны Анализ педагогической деятельности
Анализ педагогической деятельности Дополнительные цвета
Дополнительные цвета УНИВЕРСИТЕТСКАЯ БИБЛИОТЕКА В ИНФОРМАЦИОННО-ОБРАЗОВАТЕЛЬНОЙ СРЕДЕ Опарина О. Д., г. Екатеринбург, Уральский государственный униве
УНИВЕРСИТЕТСКАЯ БИБЛИОТЕКА В ИНФОРМАЦИОННО-ОБРАЗОВАТЕЛЬНОЙ СРЕДЕ Опарина О. Д., г. Екатеринбург, Уральский государственный униве Макарова Ольга Всеволодовна
Макарова Ольга Всеволодовна  Our impact
Our impact 5_Biologicheskaya_rol_elementov_7_gruppy_i_tyazhyolykh_metallov
5_Biologicheskaya_rol_elementov_7_gruppy_i_tyazhyolykh_metallov Презентация на тему Весна пришла (3 класс)
Презентация на тему Весна пришла (3 класс) Ошибки топ-менеджеров ведущих корпораций. Анализ и практические выводы
Ошибки топ-менеджеров ведущих корпораций. Анализ и практические выводы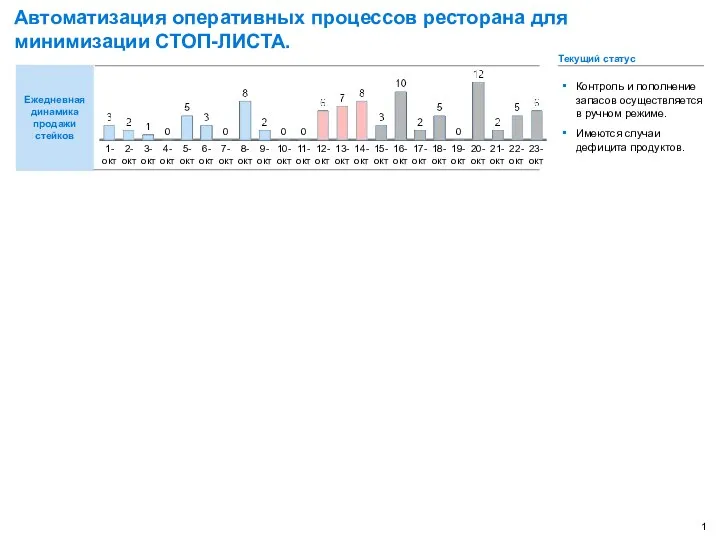 Автоматизация оперативных процессов ресторана для минимизации СТОП-ЛИСТА
Автоматизация оперативных процессов ресторана для минимизации СТОП-ЛИСТА Мертвое поле И.Васнецов
Мертвое поле И.Васнецов ФАКТОРЫ ИННОВАЦИОННОГО РАЗВИТИЯ СОВРЕМЕННОЙ ЭКОНОМИКИ
ФАКТОРЫ ИННОВАЦИОННОГО РАЗВИТИЯ СОВРЕМЕННОЙ ЭКОНОМИКИ Системы видеонаблюдения и сигнализации
Системы видеонаблюдения и сигнализации Влияние физических упражнений на осанку
Влияние физических упражнений на осанку Сельское хозяйство животноводство земледелие Овощи – овощеводство Плоды - плодоводство Поле - полеводство Лес - лесоводство Цветы
Сельское хозяйство животноводство земледелие Овощи – овощеводство Плоды - плодоводство Поле - полеводство Лес - лесоводство Цветы