Содержание
- 2. н о м ер а (1;1) (1;2) (1;3) (1;4) (1;5) …… (1;m)… г о (2;1) (2;2)
- 3. Какое это имеет отношение к математике?
- 4. Есть ли множество, мощность которого больше счетного?
- 5. Возвращаемся к Йоне Тихому. Его проживанию в гостинице пришел конец, так ее счета арестовали налоговые органы.
- 6. 101010… Директор был доволен, на каждой двери гостиничного номера красовался один из вариантов, все было готово
- 7. Какого же было его удивление, когда шеф налоговой полиции сразу указал вариант, который не был указан.
- 8. Полученного числа нет среди прибитых, потому что оно отличается от I первой цифрой, от II –
- 9. Пусть у нас выписаны все десятичные дроби с целой частью равной 0. Докажем, что мы всегда
- 11. Скачать презентацию








 Всероссийский Батюшка
Всероссийский Батюшка Презентация на тему Женские образы в романе Шолохова «Тихий Дон»
Презентация на тему Женские образы в романе Шолохова «Тихий Дон» Beach Rotana Abu-Dhabi 5* в центре деловой части Абу Даби
Beach Rotana Abu-Dhabi 5* в центре деловой части Абу Даби Механическая кулинарная обработка и нарезка овощей
Механическая кулинарная обработка и нарезка овощей Наш семейный дом
Наш семейный дом Базы данных
Базы данных Учебно-методический комплект «ОБЩЕСТВОЗНАНИЕ. ГЛОБАЛЬНЫЙ МИР В XXI ВЕКЕ»
Учебно-методический комплект «ОБЩЕСТВОЗНАНИЕ. ГЛОБАЛЬНЫЙ МИР В XXI ВЕКЕ» Искусство разрабатывать и воплощать проекты
Искусство разрабатывать и воплощать проекты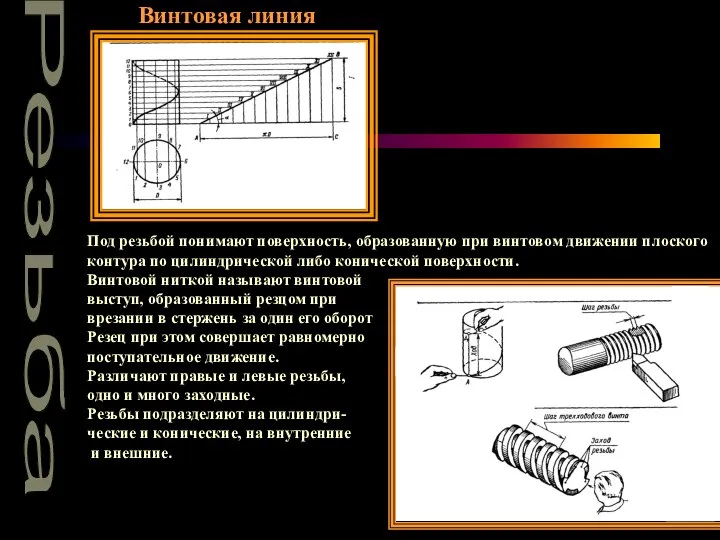 Винтовая линия
Винтовая линия Бамбук шаблон
Бамбук шаблон Инструкция по работе в сервисе PhotoPeach Автор: Бутусова В.Н.
Инструкция по работе в сервисе PhotoPeach Автор: Бутусова В.Н. Презентация на тему День Победы (9 мая 1945)
Презентация на тему День Победы (9 мая 1945) Реестр
Реестр Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты
Правила оформления чертежей ЕСКД. Форматы, масштабы, линии, шрифты 7
7 «Государственное и муниципальное управление»
«Государственное и муниципальное управление» Freelancer* или студия?
Freelancer* или студия? Отравляющие вещества
Отравляющие вещества бесплатные тесты и учебные курсы, онлайн-репетитор
бесплатные тесты и учебные курсы, онлайн-репетитор Популяризация культурного наследия калмыков средствами массовой культуры
Популяризация культурного наследия калмыков средствами массовой культуры Отчет по площадке Май 2012
Отчет по площадке Май 2012 Воспитательное пространство образовательной организации
Воспитательное пространство образовательной организации Современные средства поражения и их поражающие факторы
Современные средства поражения и их поражающие факторы Информационно-статистический обзор коллективных и индивидуальных обращений граждан за 2011 год
Информационно-статистический обзор коллективных и индивидуальных обращений граждан за 2011 год Презентация на тему "Зачем животным хвосты" - скачать презентации по Педагогике
Презентация на тему "Зачем животным хвосты" - скачать презентации по Педагогике Vzaimootnoshenie_podrostka_i_roditeley
Vzaimootnoshenie_podrostka_i_roditeley Административная школа менеджмента
Административная школа менеджмента Узники концлагерей
Узники концлагерей