Фигуры вращения

Содержание моей презентации:
Цилиндр
Конус и усечённый конус
Шар и сфера

Цилиндр
Определение.
Тело, которое образуется при вращении прямоугольника вокруг прямой, содержащей его сторону, называется цилиндром.

Круговой прямой цилиндр

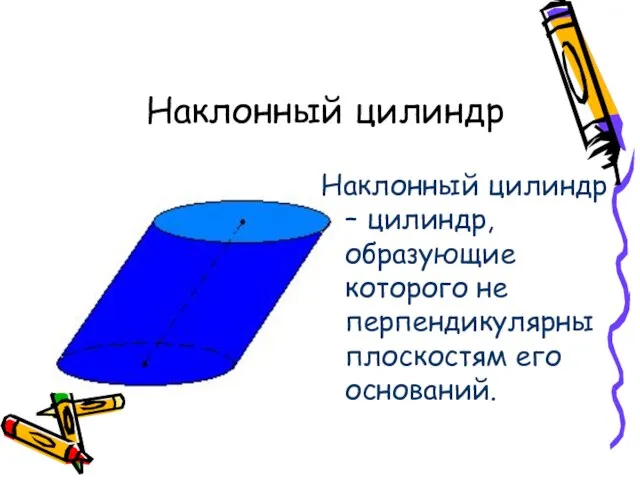
Наклонный цилиндр
Наклонный цилиндр – цилиндр, образующие которого не перпендикулярны плоскостям его оснований.

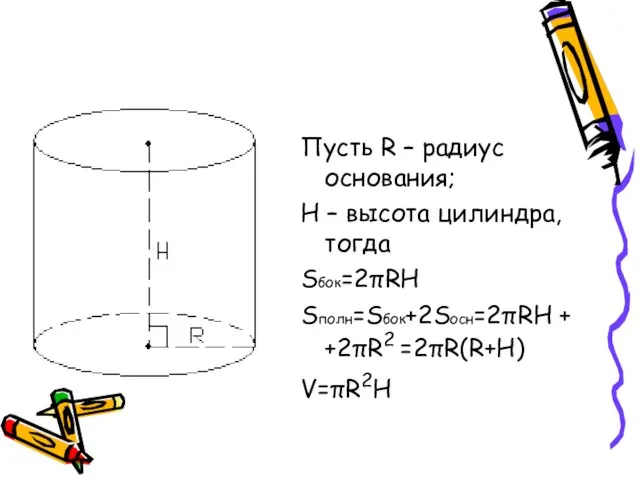
Пусть R – радиус основания;
H – высота цилиндра, тогда
Sбок=2πRH
Sполн=Sбок+2Sосн=2πRH + +2πR2 =2πR(R+H)
V=πR2H
Основные формулы

Конус
Определение:
Тело, которое образуется при вращении прямоугольного треугольника вокруг прямой, содержащий его катет, называется прямым круговым конусом.

Прямой круговой конус

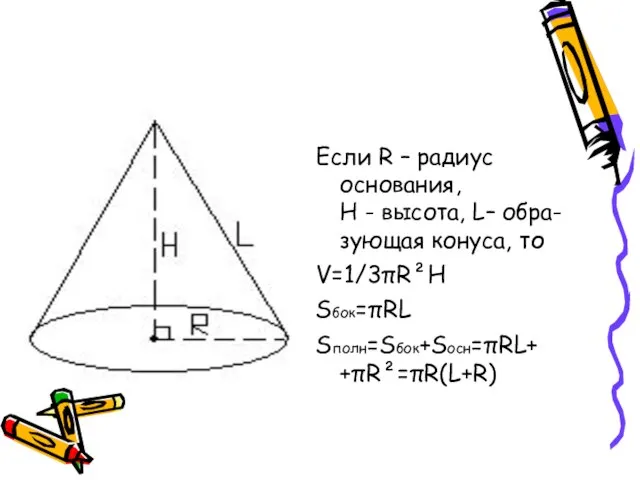
Если R – радиус основания, H - высота, L– обра- зующая конуса, то
V=1/3πR²H
Sбок=πRL
Sполн=Sбок+Sосн=πRL+ +πR²=πR(L+R)
Основные формулы

Усеченный конус
Часть конуса, ограниченная его основанием и сечением, параллельным плоскости основания, называется усеченным конусом.

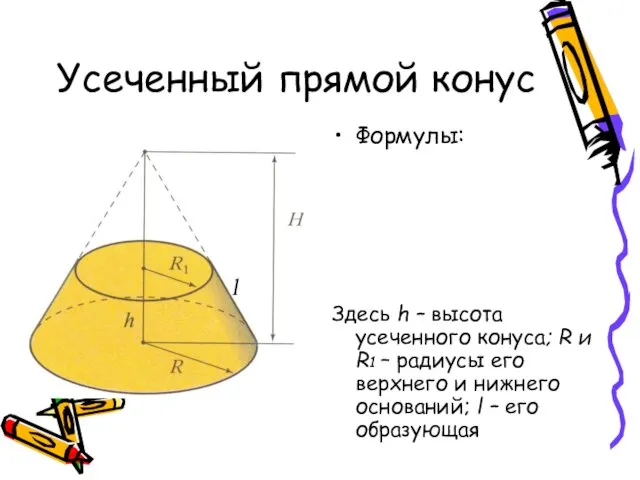
Усеченный прямой конус
Формулы:
Здесь h – высота усеченного конуса; R и R1 – радиусы его верхнего и нижнего оснований; l – его образующая

Шар и сфера
Определение.
Фигура, полученная в результате вращения полукруга вокруг диаметра, называется шаром. Поверхность, образуемая при этом полуокружностью, называется сферой.

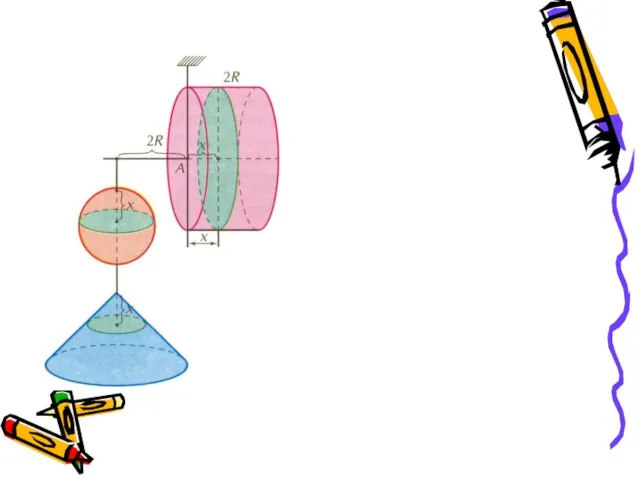
Шар – тело вращения
OS, ON, OC, OD – радиусы;
NS, CD – диаметры шара;
C и D, N и S – диаметрально противоположные точки

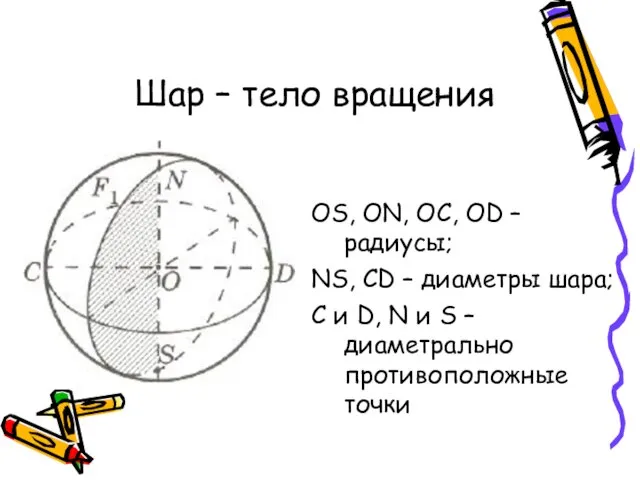
Как Архимед находил объем шара
Площади сечений:
Sц, Sш, Sк.
Sц=4πR²;
Sш=π[CE]², где [CE]²=[EO]²-[OC]²=R²- -(x-R)²=2Rx-x²;
Sк=π[CD]²= πx²

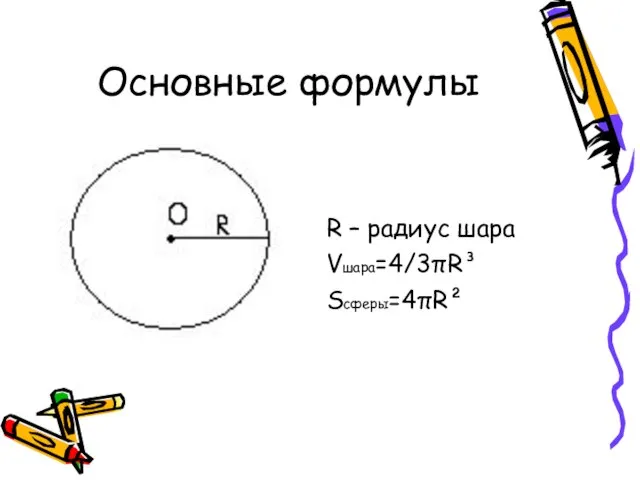
Основные формулы
R – радиус шара
Vшара=4/3πR³
Sсферы=4πR²

Уравнение сферы
Пусть A – центр(a; b; c)
MA – радиус, тогда
MA²=(x-a)²+(y-b)²+(z-c)²;
(x-a)²+(y-b)²+(z-c)²=R²