Финансово-математический аппарат динамических методов оценки экономической эффективности

Финансово-математический аппарат, который базируется на 4-х основных моментах:
I. Начисление процентов на сегодняшние платежи и определение конечной стоимости капитала эквивалентной начальному платежу
II. Определение в начале планового горизонта платежа эквивалентного заданному конечному платежу
III. Определение в начале планового горизонта платежа эквивалентного заданному ряду платежей
IV. Определение в конце планового горизонта платежа эквивалентного заданному ряду платежей

I. НАЧИСЛЕНИЕ ПРОЦЕНТОВ НА СЕГОДНЯШНИЕ ПЛАТЕЖИ И ОПРЕДЕЛЕНИЕ КОНЕЧНОЙ СТОИМОСТИ КАПИТАЛА Кn ЭКВИВАЛЕНТНОЙ НАЧАЛЬНОМУ ПЛАТЕЖУ К0
Начисление процентов на сегодняшние платежи заключается в определении величины Кn, которая будет получена на основе первоначального платежа К0, вложенного на n-периодов при заданной процентной ставке доходов на капитал. Рассмотрим динамику стоимости капитала во времени:
Для решения вопроса необходимо рассмотреть развитие капитала во времени.

II. ОПРЕДЕЛЕНИЕ В НАЧАЛЕ ПЛАНОВОГО ГОРИЗОНТА ПЛАТЕЖА К0 ЭКВИВАЛЕНТНОГО ЗАДАННОМУ КОНЕЧНОМУ ПЛАТЕЖУ Кn.
Определение первоначального платежа К0 по заданному конечному платежу Кn графически можно представить в виде:

Коэффициент дисконтирования позволяет определить в предыдущих периодах планового горизонта эквивалент платежа осуществляемого в последующих периодах. Эта процедура называется дисконтированием.

III. ОПРЕДЕЛЕНИЕ В НАЧАЛЕ ПЛАНОВОГО ГОРИЗОНТА ПЛАТЕЖА К0 ЭКВИВАЛЕНТНОГО ЗАДАННОМУ РЯДУ ПЛАТЕЖЕЙ q
Задачу определения первоначального платежа К0 эквивалентного заданному ряду платежей q, имеющих место в конце каждого промежуточного периода, графически можно представить следующим образом:

Ежегодные платежи могут быть приведены в нулевую точку с помощью ранее рассмотренного коэффициента дисконтирования.
Подобные расчеты с использованием коэффициента дисконтирования применимы при неравномерных рядах, где ежегодные платежи отличаются друг от друга. Однако такие расчеты являются громоздкими и требуют упрощения для равномерных платежных рядов, которые преобразуются на основе геометрической прогрессии в формулу:
КСД используется только для равномерных рядов, где ежегодные платежи одинаковы, для схемы постнумерандо, когда платеж осуществляется в конце временного периода.

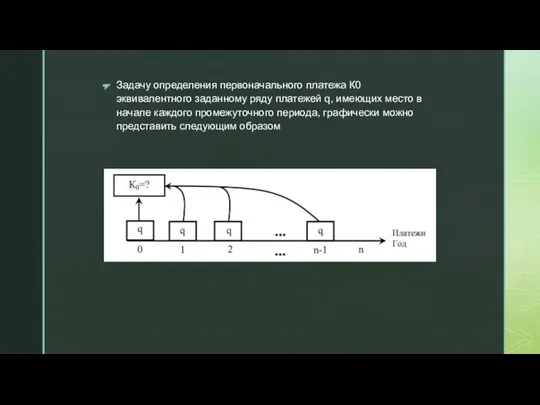
Задачу определения первоначального платежа К0 эквивалентного заданному ряду платежей q, имеющих место в начале каждого промежуточного периода, графически можно представить следующим образом

Ежегодные платежи могут быть приведены в нулевую точку с помощью ранее рассмотренного коэффициента дисконтирования.
Подобные расчеты с использованием коэффициента дисконтирования применимы при неравномерных рядах, где ежегодные платежи отличаются друг от друга.
Преобразовав уравнение:

IV. Определение в конце планового горизонта платежа эквивалентного заданному ряду платежей
Начисление процентов и определение конечной стоимости платежа Кn эквивалентного заданному ряду платежей q, имеющих место в конце соответствующих промежуточных периодов, осуществляется по схеме

Коэффициент конечной стоимости:
ККС применяется только относительноравномерных рядов.
Для неравномерных рядов используется КД (коэффициента дисконтирования).

Начисление процентов и определение конечной стоимости платежа Кn эквивалентной заданному ряду платежей q осуществляется также по схеме пренумерандо, если платежи имеют место в начале соответствующих промежуточных периодов:

Применение обозначенных инструментов в дальнейшем позволит грамотно оценивать эффективность конкретных инвестиционных и инновационных проектов, реализуемых на предприятии.
Коэффициент конечной стоимости: