Физика атома, атомного ядра

Оптико-механическая аналогия
Геометрическая
оптика
Волновая
оптика
Теоретическая
механика
Волновая
(квантовая)
механика

Оптико-механическая аналогия
Между этими двумя принципами имеется аналогия, если предположить, что
где v - фазовая скорость волны.
Геометрическая
оптика
Принцип наименьшего
времени Ферма
(Fermat P.)
Теоретическая
механика
Принцип наименьшего
действия Мопертюи (Maupertuis P.)

Гипотеза де-Бройля
Де-Бройль (de Broglie L.) предположил, что коэффи-циент пропорциональности в формуле, связываю-щей импульс и фазовую скорость, такой же, как и для фотона, т.е. равен hν :
или
где ν - линейная частота.
Это же соотношение можно записать в виде
(4.1)
где - волновое число, равное числу длин
волн, укладывающихся на отрезок 2π.

Далее, движение материальной частицы характери-зуется четырехмерным вектором энергии-импуль-са {iE/c, px, py, pz}, а плоская волна - совокупнос-тью четырех величин {iω/c, kx, ky, kz}, которые также образуют четырехвектор. Поэтому коэффи-циент пропорциональности между энергией и час-тотой, согласно гипотезе де-Бройля, также дол-жен быть таким же, как в оптике:
(4.2)
где ω - циклическая частота, связанная с линейной частотой соотношением ω = 2πν.
Формулы (4.1) и (4.2) иногда называют уравнениями де Бройля.

Волны де-Бройля
Итак, согласно гипотезе де-Бройля (1924г), микро-частицы обладают волновыми свойствами. Дли-на волны микрочастицы (электрона, протона, нейтрона, альфа-частицы и др.) называется дебройлевской длиной волны и определяет-ся формулой де Бройля:
(4.3)
где h – постоянная Планка, р – импульс частицы.

Плоская волна с амплитудой А, частотой ω и вол-новым вектором k может быть представлена в комплексной форме в виде функции
(4.4)
Фазовой скоростью волны называется скорость, с которой движутся точки волны с постоянной фазой. Если ось x направлена по вектору p, то условие постоянства фазы
Et - px = const. (4.5)
Чтобы вычислить фазовую скорость, надо про-дифференцировать это уравнение по времени.

Продифференцируем (4.5) по времени:
откуда
(4.6)
где v - скорость частицы, которая определяется групповой скоростью волн де-Бройля:
(4.7)

Из формулы (4.6) следует, что фазовая скорость волн де-Бройля всегда больше скорости света (т.к. скорость частицы v всегда меньше скорости све-та). Это, однако, не противоречит теории относи-тельности, т.к. фазовая скорость не характеризует ни скорость перемещения массы, ни скорость пе-ремещения энергии.
Сравнивая (4.6) и (4.7), приходим к важному и уни-версальному соотношению между фазовой ско-ростью волн де-Бройля и скоростью частицы:
vф⋅vг = с2 (4.8)

Гипотеза де-Бройля
и правило квантования Бора
Пользуясь понятием дебройлевской длины волны, можно дать наглядное истолкова-ние правилу квантования круговых орбит. Электрон обладает волновыми свойства-ми. Чтобы энергия волнового движения не распространялась в другие области (т.е. чтобы электрон при движении вокруг ядра не излучал энергию), волна должна быть стоячей.

На круговой орбите стоячая волна возни-кает, если на этой орбите уложится целое число длин волн де-Бройля: nλ=2πr. Отсюда, учитывая, что
λ = h/mv,
находим:
L = mvr = nh/2π = n,
т.е. правило квантования.
Таким образом, 1-ый постулат Бора – логическое следствие волновой природы электрона.

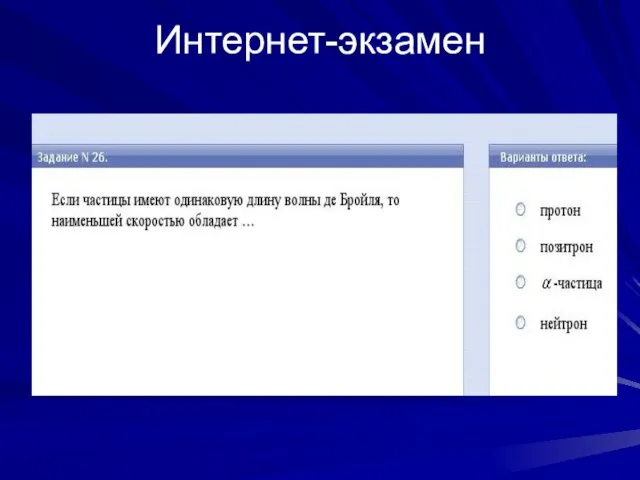
Интернет-экзамен
Длина волны де Бройля частицы уменьши-лась вдвое. Скорость этой частицы …
ВАРИАНТЫ ОТВЕТОВ:
1) не изменилась
2) уменьшилась в 4 раза
3) увеличилась в 4 раза
4) уменьшилась вдвое
5) увеличилась вдвое

Интернет-экзамен

Интернет-экзамен