Содержание
- 2. Исходные данные и порядок формирования вер.-стат. модели эксплуатации Эксплуатация авиационной техники (АТ) – это целенаправленная деятельность
- 3. Исходные данные и порядок формирования вер.-стат. модели эксплуатации Исходными данными для формирования вер.-стат. модели являются экспериментальные
- 4. Законы распределения непрерывных случайных величин, используемые при формировании вер.-стат. моделей В практике эксплуатации АТ встречаются следующие
- 5. Нормальное распределение Нормальному распределению приближенно соответствует распределение суммарной наработки восстанавливаемого изделия до капитального ремонта. Общий вид
- 6. Экспоненциальное распределение Экспоненциальное распределение встречается после окончания периода приработки (в период нормальной эксплуатации), когда поток отказов
- 7. Экспоненциальное распределение Плотность распределения вероятностей в случае экспоненциального распределения имеет вид: Экспоненциальный закон является однопараметрическим, параметр
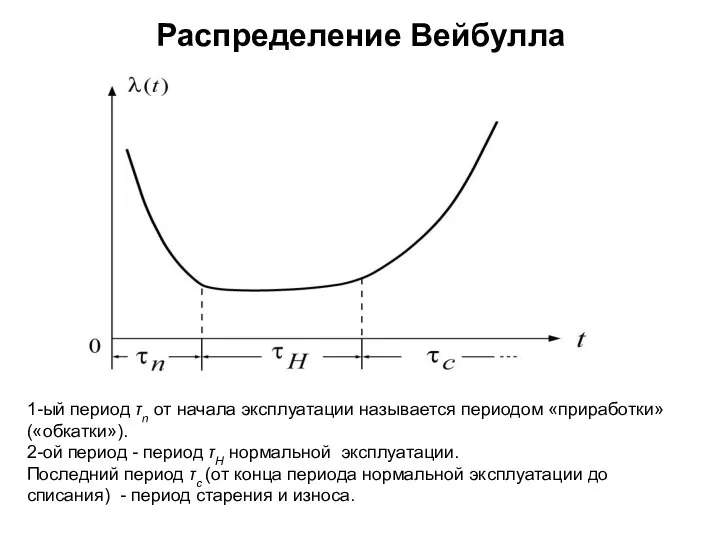
- 8. Распределение Вейбулла Распределение Вейбулла часто используется в теории надежности. Законом Вейбулла описывается наработка до отказа у
- 9. Распределение Вейбулла 1-ый период τn от начала эксплуатации называется периодом «приработки» («обкатки»). 2-ой период - период
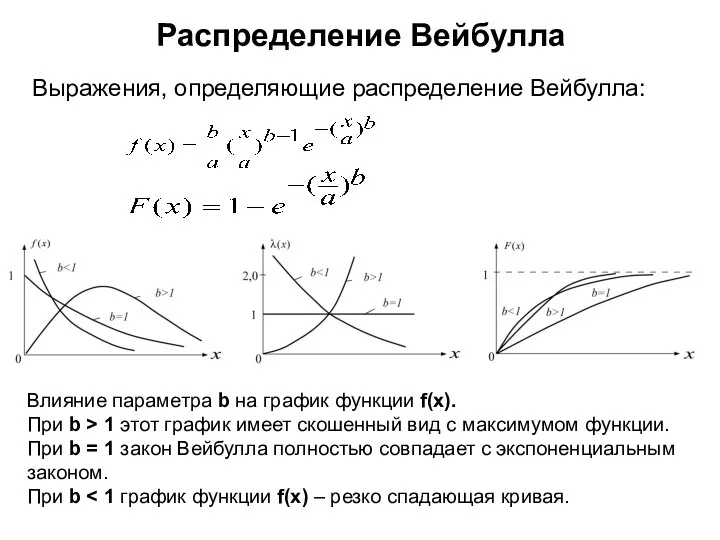
- 10. Распределение Вейбулла Выражения, определяющие распределение Вейбулла: Влияние параметра b на график функции f(x). При b >
- 11. Гамма-распределение Гамма-распределение может встречаться в следующих случаях : - этому распределению подчиняется иногда время восстановления; -
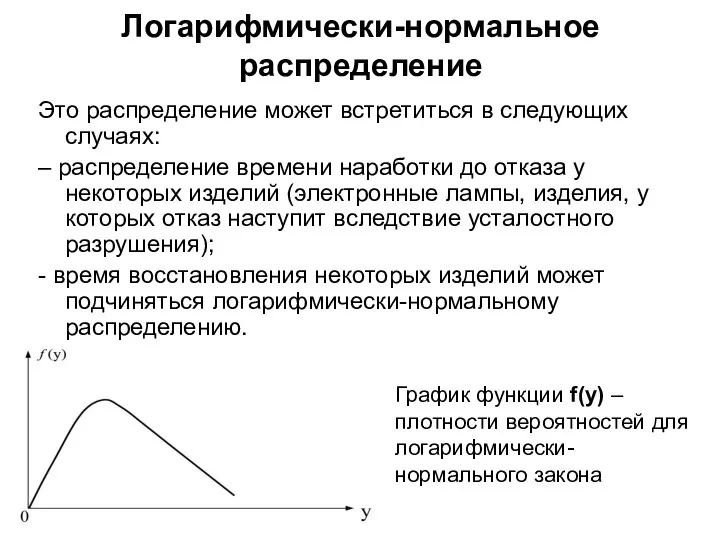
- 12. Логарифмически-нормальное распределение Это распределение может встретиться в следующих случаях: – распределение времени наработки до отказа у
- 14. Скачать презентацию








 Модерн
Модерн Художественные работы
Художественные работы www.marketing.rbc.ru
www.marketing.rbc.ru ИТ инфраструктура колледжа (для студентов)
ИТ инфраструктура колледжа (для студентов) Размеры и оборудование баскетбольной площадки
Размеры и оборудование баскетбольной площадки Рынок ценных бумаг
Рынок ценных бумаг Знаю, что горцам, Хоть нравы их строги,В облачном крае скалистых земельПесня нужна, словно лошадь В дороге,Песня н
Знаю, что горцам, Хоть нравы их строги,В облачном крае скалистых земельПесня нужна, словно лошадь В дороге,Песня н Каша - радость наша
Каша - радость наша Khudozhestvennaya_obrabotka_dereva
Khudozhestvennaya_obrabotka_dereva Введение стандартов ISO на системы менеджмента в практику российской компанииКейс в продолжение доклада «Международные ст
Введение стандартов ISO на системы менеджмента в практику российской компанииКейс в продолжение доклада «Международные ст Однофазные линейные электрические цепи синусоидального тока. Электродвижущие силы, напряжения и токи
Однофазные линейные электрические цепи синусоидального тока. Электродвижущие силы, напряжения и токи Рациональный потребительский бюджет
Рациональный потребительский бюджет Интегрированное производство шприцев III поколения с усовершенствованной иглой для внутримышечных инъекций
Интегрированное производство шприцев III поколения с усовершенствованной иглой для внутримышечных инъекций Социально-значимое проектирование в формировании метапредметных компетенций в условиях перехода к ФГОС ООО
Социально-значимое проектирование в формировании метапредметных компетенций в условиях перехода к ФГОС ООО Развитие творческого мышления на урокахинформатики.
Развитие творческого мышления на урокахинформатики. Presentation Title Here
Presentation Title Here 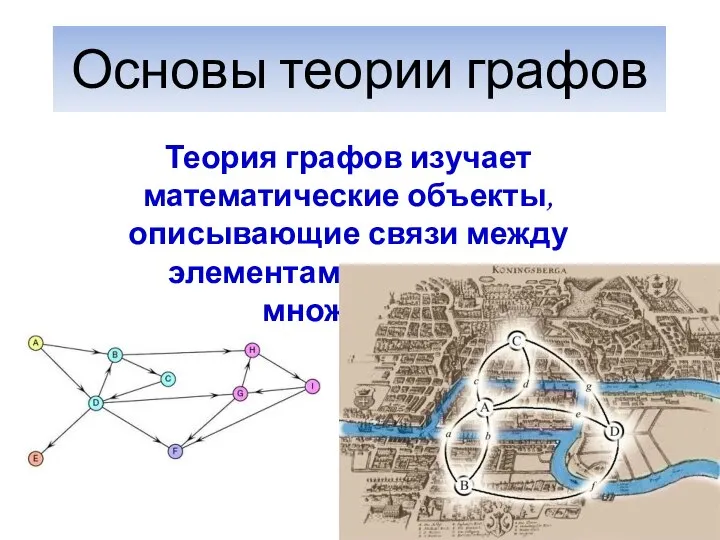 Основы теории графов
Основы теории графов source(3)
source(3) «1С:Подрядчик строительства 3.0. Управление строительным производством»
«1С:Подрядчик строительства 3.0. Управление строительным производством» Газгольдеры. Газгольдеры для нефтебаз
Газгольдеры. Газгольдеры для нефтебаз Особенности проведения государственной (итоговой) аттестации выпускников общеобразовательных учреждений в 2012 году
Особенности проведения государственной (итоговой) аттестации выпускников общеобразовательных учреждений в 2012 году Символические образы в романе И.А. Гончарова «Обломов»
Символические образы в романе И.А. Гончарова «Обломов» Деление
Деление  Венера в знаках Зодиака
Венера в знаках Зодиака Fairy Pairs. Площадки для рекламы
Fairy Pairs. Площадки для рекламы Автоматизация водоснабжения
Автоматизация водоснабжения Презентация на тему КВН по сказкам Пушкина
Презентация на тему КВН по сказкам Пушкина Разбор статьи 7 нестандартных решений в бизнесе
Разбор статьи 7 нестандартных решений в бизнесе