Г) 29; -28;27; -26;…
№2Выберите последовательность, которая НЕ
является арифметической прогрессией
А) 1;2;3;4… Б) -10; -9; -7;-4;0;5;….
В) -3; -8; -13; -18;…Г) 1,2; 2,7; 4,2…
№3 Найдите разность арифметической
прогрессии 15;30;45;…
А) 15 Б) -15 В) 2 Г) ½
№4 Найдите сумму первых восьми членов
арифметической прогрессии, если известно, что
её первый член равен -4, а разность равна 2
А) 12 Б) 10 В) 24 Г) 32
№5 Найдите пятый член арифметической
прогрессии, если ее первый член равен 7, а
разность равна -2
А) -3 Б) -1 В) 0,4375 Г) 112
Вариант 2
№1Выберите последовательность, которая
является арифметической прогрессией
А) 7;14;-7;-14;14;21… Б) -8;-5;-2;…
В) -40;-39;-38;38;39;40;-37;-36; ….
Г)-7;2;-6;3;-5;4;…
№2Выберите последовательность, которая НЕ
является арифметической прогрессией
А) 10;20;30;40… Б) 6;4;8/3;16/9;….
В)7,5;5,5;3,5;1,5;… Г) 3;6;9;12;…
№3 Найдите разность арифметической
прогрессии 4;8;12;16....
А) 2 Б) 1/2 В) -4 Г) 4
№4 Найдите сумму первых десяти членов
арифметической прогрессии, если известно, что
её первый член равен -7, а разность равна 3
А) 65 Б) 23 В) 80 Г) 20
№5 Найдите девятый член арифметической
прогрессии, если ее первый член равен 3, а
разность равна 0,5
А) 7,5 Б) 7 В) 768 Г) 0,01171875










 Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Информационное оснащение женских консультаций
Информационное оснащение женских консультаций Презентация на тему Сложение чисел с помощью координатной прямой
Презентация на тему Сложение чисел с помощью координатной прямой  Что такое натуральные ткани? каковы их свойства?
Что такое натуральные ткани? каковы их свойства? Неорганические кислоты
Неорганические кислоты Фторхинолоны клиническая фармакология иособенности действия
Фторхинолоны клиническая фармакология иособенности действия ИГРА С БУДУЩИМ
ИГРА С БУДУЩИМ Антонио Гауди - великий архитектор
Антонио Гауди - великий архитектор Сообщающиеся сосуды
Сообщающиеся сосуды Плавание тел
Плавание тел Любимые места отдыха
Любимые места отдыха Повседневная жизнь земледельцев и горожан в средние века
Повседневная жизнь земледельцев и горожан в средние века Сводный медиаплан рекламной кампании
Сводный медиаплан рекламной кампании Лагерь молодёжного актива
Лагерь молодёжного актива Повесть Н.С.Лескова «Очарованный странник»
Повесть Н.С.Лескова «Очарованный странник» Мельник М.В. Управление риском
Мельник М.В. Управление риском Ошибки вокруг нас
Ошибки вокруг нас Приблизительные размеры территорий
Приблизительные размеры территорий Chanel SS21. Alberta Ferretti SS21. Вдохновение
Chanel SS21. Alberta Ferretti SS21. Вдохновение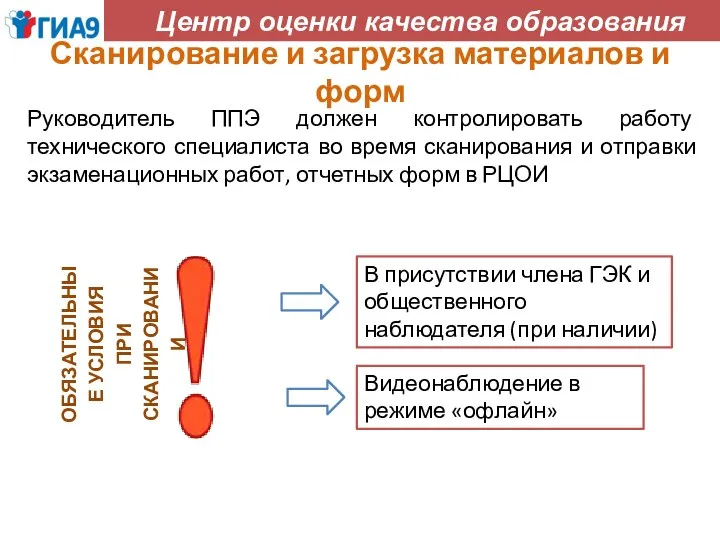 Обязательные условия при сканировании
Обязательные условия при сканировании chekhov
chekhov Презентация на тему Происхождение рас
Презентация на тему Происхождение рас  Обзор Информационно-аналитической системы «Семантический архив» 3.0
Обзор Информационно-аналитической системы «Семантический архив» 3.0 ГАЗЕТАК ПРАЗДНИКУ «ДЕНЬ МАТЕРИ»
ГАЗЕТАК ПРАЗДНИКУ «ДЕНЬ МАТЕРИ» Презентация на тему Памятник русскому солдату в Болгарии
Презентация на тему Памятник русскому солдату в Болгарии Как маркетинговая аналитика увеличивает продажи. Часть 1
Как маркетинговая аналитика увеличивает продажи. Часть 1 აუდიტი გამა
აუდიტი გამა Изделия из бересты
Изделия из бересты