Содержание
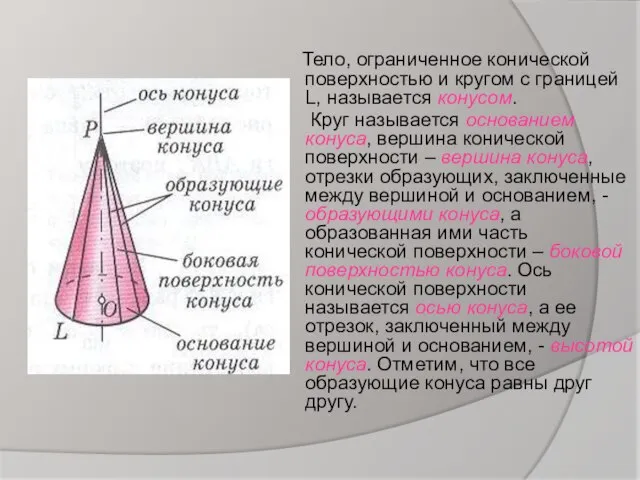
- 2. Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом. Круг называется основанием конуса, вершина
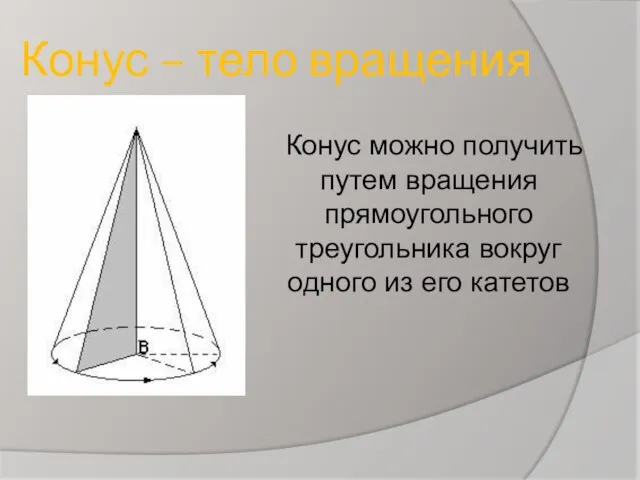
- 3. Конус – тело вращения Конус можно получить путем вращения прямоугольного треугольника вокруг одного из его катетов
- 4. Площадь боковой поверхности конуса Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
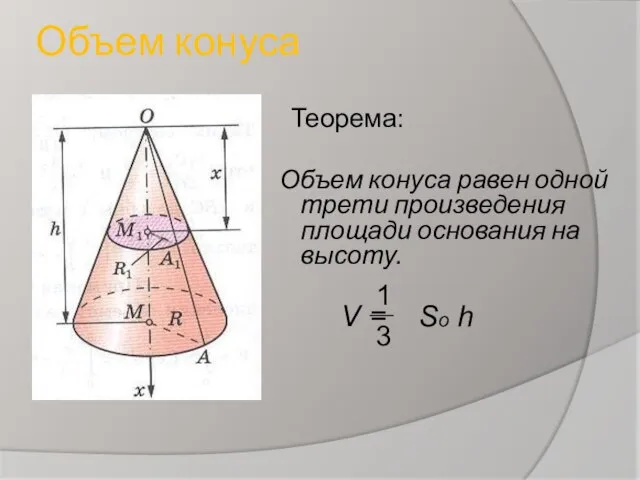
- 5. Объем конуса Теорема: Объем конуса равен одной трети произведения площади основания на высоту. V = So
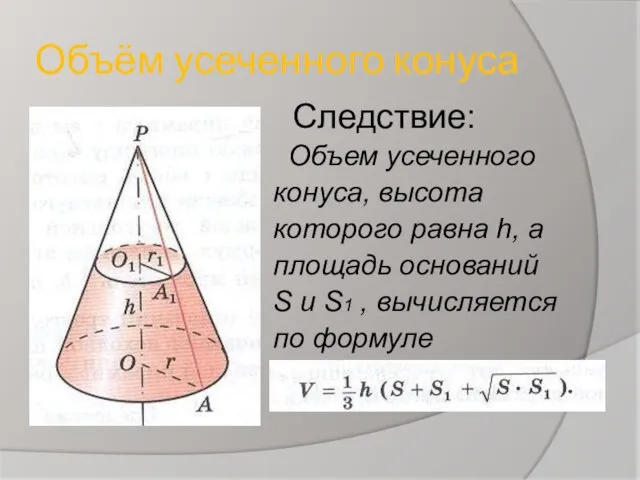
- 6. Объём усеченного конуса Следствие: Объем усеченного конуса, высота которого равна h, а площадь оснований S и
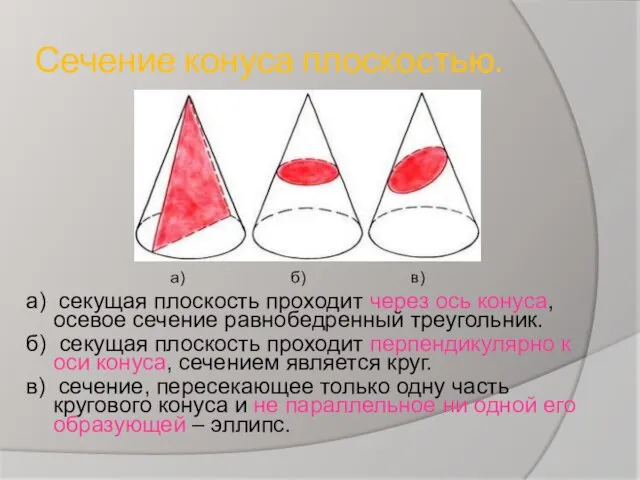
- 7. Сечение конуса плоскостью. а) секущая плоскость проходит через ось конуса, осевое сечение равнобедренный треугольник. б) секущая
- 9. Скачать презентацию

 Презентация на тему Формирование современной образовательной инфраструктуры: новые подходы, модели
Презентация на тему Формирование современной образовательной инфраструктуры: новые подходы, модели Алканы
Алканы ЦКП «Курчатовский центр синхротронного излучения и нанотехнологий (КЦСИиНТ)»
ЦКП «Курчатовский центр синхротронного излучения и нанотехнологий (КЦСИиНТ)» Глобальные экологические проблемы
Глобальные экологические проблемы Кастинг телеведущих
Кастинг телеведущих ЦЕНТР ОБРАЗОВАНИЯ №2045
ЦЕНТР ОБРАЗОВАНИЯ №2045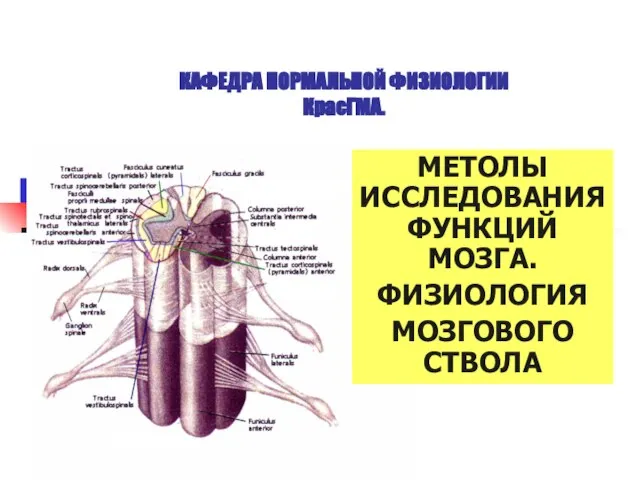 Презентация на тему Исследовние функций мозга. Физиология мозгового ствола
Презентация на тему Исследовние функций мозга. Физиология мозгового ствола  Выполнение вышивки двусторонней гладью
Выполнение вышивки двусторонней гладью Презентация на тему Числовые выражения 6-7 класс
Презентация на тему Числовые выражения 6-7 класс 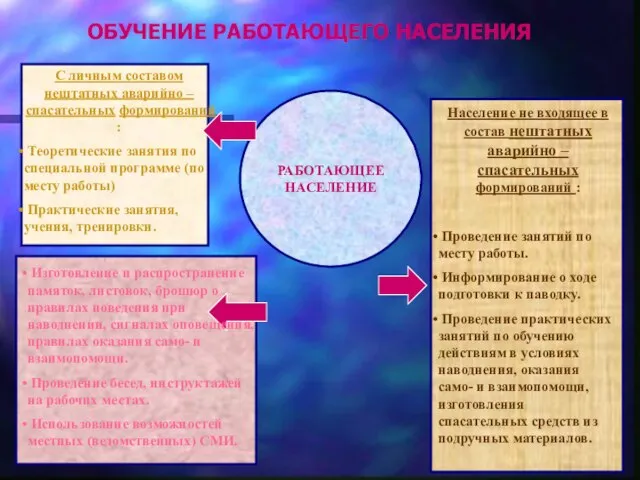 ОБУЧЕНИЕ РАБОТАЮЩЕГО НАСЕЛЕНИЯ
ОБУЧЕНИЕ РАБОТАЮЩЕГО НАСЕЛЕНИЯ Аренда. Определение, понятие и юридическая характеристика договора аренды
Аренда. Определение, понятие и юридическая характеристика договора аренды Урок русского языка в 5 классе
Урок русского языка в 5 классе МОУ«Основная общеобразовательная школа № 3» г. Оренбурга 2008-2009
МОУ«Основная общеобразовательная школа № 3» г. Оренбурга 2008-2009 Презентация проекта по теме: «Творческий портрет М.Танаевой»
Презентация проекта по теме: «Творческий портрет М.Танаевой» Мы за все в ответе…
Мы за все в ответе… Презентация на тему Атомная энергетика и ее экологические проблемы
Презентация на тему Атомная энергетика и ее экологические проблемы Основы информатики и программирования
Основы информатики и программирования Теория фирмы и теория транзакционных издержек
Теория фирмы и теория транзакционных издержек Портфолио
Портфолио Естественный отбор и его формы
Естественный отбор и его формы Физическая культура в наших семьях
Физическая культура в наших семьях Презентация на тему Дети блокадного Ленинграда
Презентация на тему Дети блокадного Ленинграда Совещание 29 марта 2012 года Исполнение действующего законодательства и нормативных актов при предоставлении платных образователь
Совещание 29 марта 2012 года Исполнение действующего законодательства и нормативных актов при предоставлении платных образователь Задачи на вычисление импульса тела.
Задачи на вычисление импульса тела. Мини волейбол в школе
Мини волейбол в школе Физкультурно-оздоровительная работа детского сада
Физкультурно-оздоровительная работа детского сада Слова, которые имеют общую часть и общее значение, называются родственными
Слова, которые имеют общую часть и общее значение, называются родственными ПЛОТНИКОВА ЕЛЕНА ВЛАДИМИРОВНА
ПЛОТНИКОВА ЕЛЕНА ВЛАДИМИРОВНА