Формулы сокращенного умножения

Цели:
Познакомиться с формулами сокращенного умножения:
квадрат суммы
квадрат разности
разность квадратов
Рассмотреть геометрический смысл формул сокращенного умножения.
Закрепить полученные знания в ходе выполнения заданий
из 56

Вы знаете, что при умножении многочлена на многочлен каждый член одного многочлена умножается на каждый член другого.
Но в некоторых случаях умножение многочленов можно выполнить короче.
из 56

Для этого нужно воспользоваться
Формулами
сокращённого
умножения
из 56

КВАДРАТ
СУММЫ
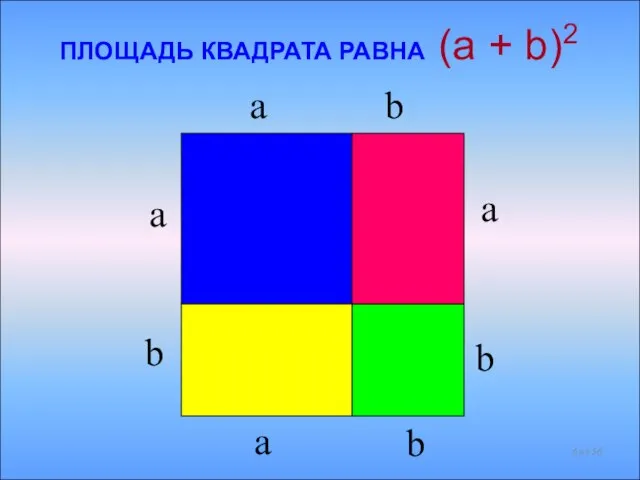
из 56

a b
a
b
a
b
a
b
ПЛОЩАДЬ КВАДРАТА РАВНА (a + b)2
из 56

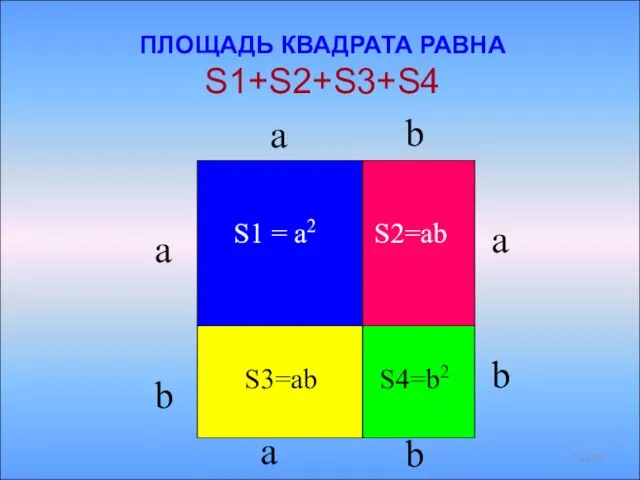
S1 = a2
S2=ab
S3=ab
S4=b2
ПЛОЩАДЬ КВАДРАТА РАВНА S1+S2+S3+S4
a
b
a
b
b
a
b
a
из 56

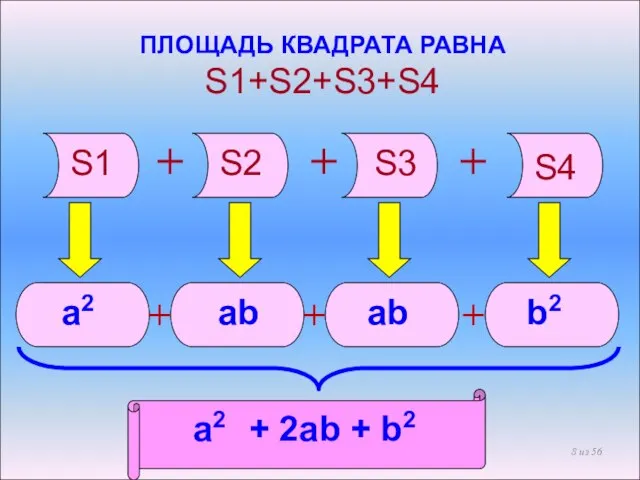
ПЛОЩАДЬ КВАДРАТА РАВНА S1+S2+S3+S4
S2
S3
S4
S1
+
+
+
а2
ab
ab
b2
а2 + 2ab + b2
+
+
+
из 56

Выразили одну и ту же площадь двумя способами
S = (a+b)2 S = a2 + 2ab + b2
из 56

(a+b)2 = a2 +2ab + b2
ПОЛУЧИЛИ
из 56

Полученное тождество
Формулой
квадрата
суммы
(a+b)2 = a2 +2ab + b2
называется из 56

Квадрат суммы двух выражений равен квадрату первого выражения, плюс удвоенное произведение первого на второе, плюс квадрат второго выражения.
(a+b)2 = a2 +2ab + b2
из 56

применения формулы квадрата суммы
Пример
Раскройте скобки в выражении
(3x + 4ky)2
из 56

применения формулы квадрата суммы
2
•
•
+
2
+
2
+
2
=
3х
4kу
3x
3x
4kу
4kу
Пример
из 56

применения формулы квадрата суммы
= 9x 2 +24xky + 16k2y2
+
2
=
3х
4kу
Пример
из 56

Возведем в квадрат сумму
7n + 4m
По формуле квадрата суммы получим:
(7n + 4m)2 =
= (7n)2 + 2  7n  4m + (4m)2 =
= 49n2 + 56nm + 16m2
из 56

Раскройте скобки в выражениях
1) (3 + 8р)2
2) ( 6х + 4)2
3) (4,2 + 0,5х)2
4) (0,3ху+k)2
из 56
= 64р2 + 48р + 9
= 36х2 + 48х + 16
= 0,25х2+4,2х+17,64
=0,09х2у2+0,6хуk+k2

КВАДРАТ
РАЗНОСТИ
из 56

Возведем в квадрат разность
a - b
(a – b) =
= (a – b)(a – b) = …
Закончите
преобразование
из 56
2

Проверьте результаты преобразований
(a – b) =
= a – 2ab + b
из 56
2
2
2

Полученное тождество
Формулой
квадрата
разности
(a – b)2 = a2 – 2ab + b2
называется
из 56

Квадрат разности двух выражений равен квадрату первого выражения, минус удвоенное произведение первого на второе, плюс квадрат второго выражения.
(a - b)2 = a2 - 2ab + b2
из 56

применения формулы квадрата разности
Раскройте скобки в выражении
(5pn – 2m)2
Пример
из 56

применения формулы квадрата разности
Пример
2
•
•
2
+
2
2
=
5pn
2m
5pn
5pn
2m
2m
из 56

применения формулы квадрата разности
Пример
= 25p2n2 - 20pnm + 4m2
2
=
5pn
2m
из 56

Возведем в квадрат разность
7х – 4у
По формуле квадрата разности получим:
(7х – 4у)2 =
= (7х)2 - 2  7х  4у + (4у)2 =
= 49х2 - 56ху + 16у2
из 56

Раскройте скобки в выражениях
1) (5х-3)2
2) (13-6р)2
3) (2,3-0,4х)2
4) (0,6ху-k)2
из 56
=25х2 – 30х + 9
=36р2–156р+169
=0,16х2–1,84х+5,29
=0,36х2у2–1,2хуk+k2

РАЗНОСТЬ
КВАДРАТОВ
из 56

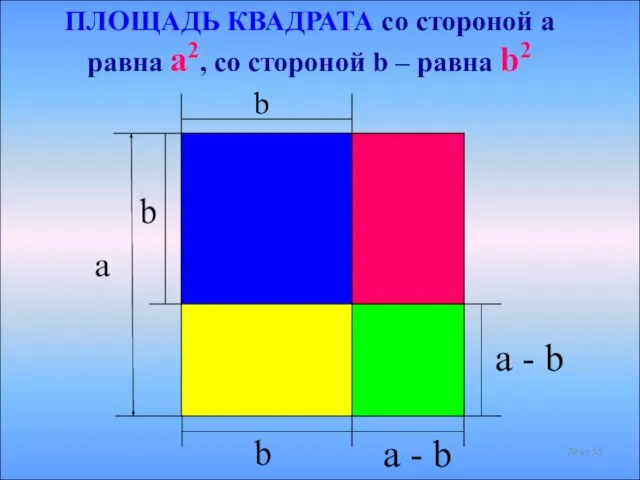
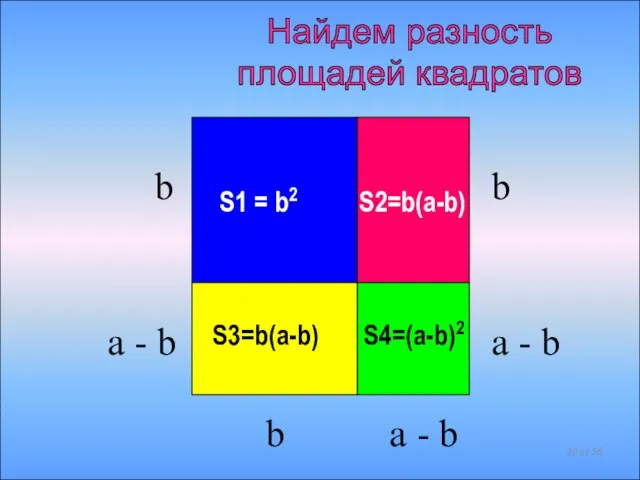
b
b
b
a - b
a - b
a
ПЛОЩАДЬ КВАДРАТА со стороной а равна а2, со стороной b – равна b2
из 56

S1 = b2
S2=b(a-b)
S3=b(a-b)
S4=(a-b)2
b
a - b
b
a - b
a - b
b
Найдем разность
площадей квадратов
из 56

S1 = b2
S2=b(a-b)
S3=b(a-b)
S4=(a-b)2
a - b
b
a - b
a - b
b
Найдем разность
площадей квадратов
из 56

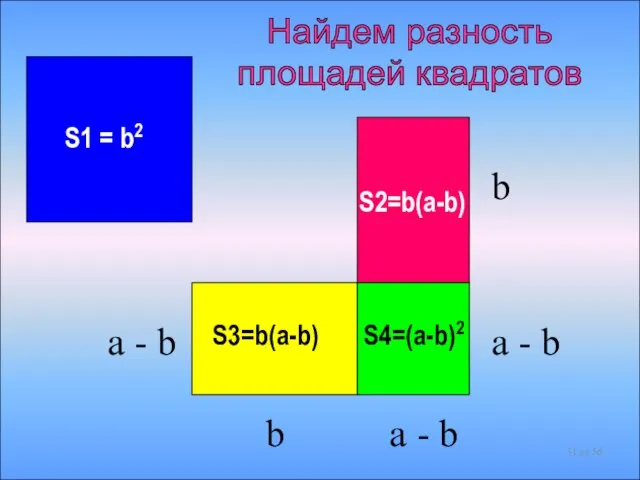
S2=b(a-b)
S3=b(a-b)
S4=(a-b)2
a - b
b
a - b
a - b
b
Разность
площадей квадратов
а - b
2
2
а - b
из 56

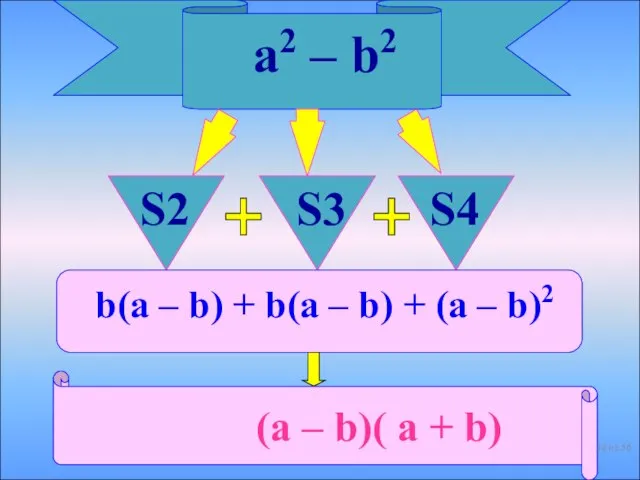
a2 – b2 = S2 + S3 + S4
S2 = b(a – b)
S3 = b(a – b)
S4 = (a – b)2
из 56

a2 – b2
S2
S3
S4
+
+
(a – b)( a + b)
b(a – b) + b(a – b) + (a – b)2
из 56

a2 – b2 = (a – b)(a + b)
ПОЛУЧИЛИ
из 56

Полученное тождество
Формулой
разности
квадратов
a2 – b2 = (a – b)(a + b)
называется
из 56

Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a2 – b2 = (a – b)(a + b)
из 56

применения формулы разности квадратов
Пример
Разложите на множители выражение
25x2 - 4y2 из 56

применения формулы разности квадратов
+
2
=
5х
2у
5x
5x
2у
2у
2
Пример
из 56

= (5x – 2у)(5х + 2у)
2
=
5х
2у
2
Пример
применения формулы разности квадратов
из 56

Разложите на множители выражение 49n2 - 4m2
По формуле разности квадратов получим:
49n2 - 4m2 =
= (7n)2 - (2m)2 =
= (7n – 2m)(7n + 2m)
из 56

Разложите на множители выражения
1) 9-16р2
2) 36х2-64
из 56
=(3 – 4p)(3 + 4p)
=(6x – 8)(6x + 8)

Попробуйте разложить на множители следующее выражение
16х8 – 9
из 56
Подсказка :
16х8 = (4х4)2

16х8 – 9=
= (4х4 – 3)(4х4 + 3)
Проверьте свои результаты
из 56

Поменяем местами правую и левую части в формуле разности квадратов.
получим:
(a – b)(a + b) = a2 – b2
из 56

Это тождество позволяет сокращенно выполнять умножение разности любых двух выражений на их сумму.
(a – b)(a + b) = a2 – b2
из 56

Выполните умножение выражений
из 56
(k–c)(k+c)
(4f+3)(4f–3)
(5d–7b)(5d+7b)
= k2 – c2
= 25d2– 49b2
= 16f 2– 9

Самое главное:
Формула квадрата суммы:
(a+b)2 = a2 +2ab + b2
Формула квадрата разности:
(a - b)2 = a2 - 2ab + b2
Формула разности квадратов:
a2 – b2 = (a – b)(a + b)
из 56

Закрепление материала
№ 33.1
№ 33.4
№ 33.14
№ 33.18 (а, б)
№ 33.20
№ 33.23
из 56

Ответим на вопросы:
1) Для чего нужны формулы сокращённого умножения?
2) Сформулируйте формулу квадрата суммы.
3) Запишите формулу квадрата суммы.
4) Сформулируйте формулу квадрата разности.
5) Запишите формулу квадрата разности.
6) Сформулируйте формулу разности квадратов.
7) Запишите формулу разности квадратов.
из 56