Формы мышления. Алгебра высказываний

Цель:
Рассмотреть основные понятия логики предикатов.

Логика – это наука о формах и способах мышления.
Логика изучает внутреннюю структуру процесса мышления, который реализуется в таких естественно сложившихся формах как понятие, суждение, умозаключение и доказательство.

Понятие.
Понятие – это форма мышления, отражающая наиболее существенные свойства предмета, отличающие его от других предметов.
В структуре каждого понятия нужно различать две стороны: содержание и объем.
Содержание понятия составляет совокупность существенных признаков предмета.
Объем понятия определяется совокупностью предметов, на которую оно распространяется, и может быть представлено в форме множества объектов, состоящего из элементов множеств.

Алгебра множеств, одна из основополагающих современных математических теорий.
Между множествами может могут быть различные виды отношений:
равнозначность, когда объемы понятий полностью совпадают
пересечение, когда объемы понятий частично совпадают
подчинение, когда объем одного понятия полностью входит в объем другого.

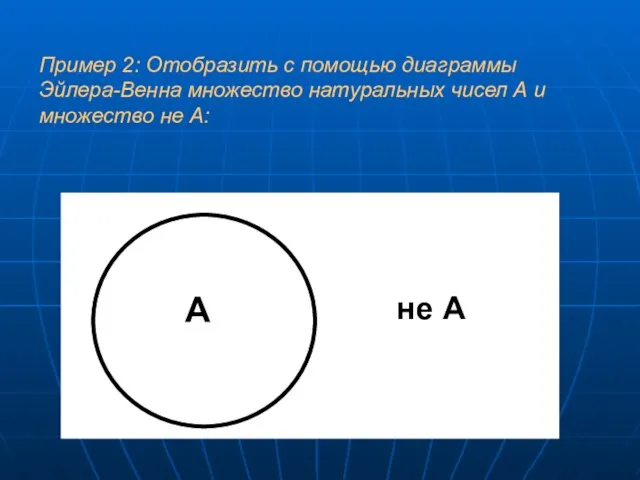
Для наглядной иллюстрации объемов понятий используются диаграммы Эйлера-Венна. Если имеются какие-либо понятия А, В, С, то объем каждого понятия (множество) можно представить в виде круга, а отношения между ними в виде пересекающихся кругов.
Пример 1: Отобразить с помощью диаграммы Эйлера-Венна соотношение между объемами понятий натуральные числа и четные числа.
Натуральные числа – это множество целых положительных чисел А, а четные – это множество отрицательных и положительных чисел B. Там, где они пересекаются получается множество натуральных четных чисел С:

А
не А
Пример 2: Отобразить с помощью диаграммы Эйлера-Венна множество натуральных чисел А и множество не А:

Высказывание – это предложение в отношении которого можно однозначно сказать истинно оно или ложно. Высказывания бывают общими, частными или единичными.

Общее высказывание начинается со слов: все, всякий, каждый, ни один.
Все кошки умеют летать
Всякий ребенок ходит в школу
Ни один ребенок не старше своей мамы
Каждая рыба умеет плавать

Частное высказывание начинается со слов: некоторые, большинство и т.п.
Некоторые птицы умеют разговаривать
Большинство людей любят мороженное

Во всех других случаях высказывание является единичным.

Высказывание может быть простым или составным.
Простое высказывание, если никакая его часть сама не является высказыванием.
Составное – это высказывание, состоящее из простых высказываний.

Высказывания имеют определенную логическую форму.
Понятие о предмете мысли называется субъектом и обозначается буквой S, а понятие о свойствах и отношениях предмета называется предикатом и обозначается буквой Р.

Оба эти понятия – субъект и предикат называются терминами суждения.
Отношения между субъектом и предикатом выражаются связкой «есть», «не есть», «является», «состоит» и т.д.
Таким образом, каждое высказывание состоит из трех элементов – субъекта, предиката и связки.
Состав суждения можно выразить общей формулой «S есть Р» или «S не есть Р».

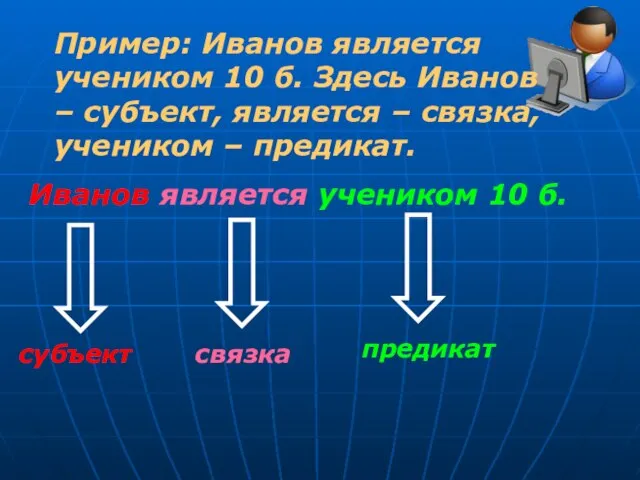
Пример: Иванов является учеником 10 б. Здесь Иванов – субъект, является – связка, учеником – предикат.
Иванов является учеником 10 б.
субъект
связка
предикат

Умозаключение.
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (вывод).
Умозаключения бывают дедуктивные, индуктивные и по аналогии.

В дедуктивных умозаключениях рассуждения ведутся от общего к частному.
Например, из двух высказываний: «Ртуть является металлом» и «Все металлы электропроводны» можно сделать вывод «Ртуть электропроводна».

В индуктивных умозаключениях рассуждения ведутся от частного к общему.
Например, установив, что отдельные металлы – железо, медь, цинк и так далее – обладают свойством электропроводности можно сделать вывод, что все металлы электропроводны.

Умозаключение по аналогии представляет собой движение мысли от общности одних свойств и отношений у сравниваемых предметов или процессов.
Например, химический состав Солнца и Земли сходен по многим показателям, поэтому, когда на Солнце нашли еще неизвестный элемент гелий, предположили, что данный элемент есть и на Земле.

Доказательство.
Доказательство – есть мыслительный процесс, направленный на подтверждение или опровержение какого либо положения посредством других несомненных, ранее обоснованных доводов.

Спасибо
за внимание!

Автор презентации:
Ширяева Ольга Мухадинновна,
Муниципальное Общеобразовательное Учреждение
«Средняя общеобразовательная школа №2»,
учитель информатики,
1 квалификационной категории.
http://www.shiryaeva.86sch2-nyagan.edusite.ru