Fractals and Chaos Theory

Chaos Theory about disorder
NOT denying of determinism
NOT denying of ordered systems
NOT announcement about useless of complicated systems
Chaos is main point of order

What is the chaos theory?
Learning about complicated nonlinear dynamic systems
Nonlinear – recursion and algorithms
Dynamic – variable and noncyclic

Wrong interpretations
Society drew attention to the chaos theory because of such movies as Jurassic Park. And because of such things people are increasing the fear of chaos theory.
Because of it appeared a lot of wrong interpretations of chaos theory

Chaos Theory about disorder
Truth that small changes could give huge consequences.
Concept: impossible to find exact prediction of condition, but it gives general condition of system
Task is in modeling the system based on behavior of similar systems.

Usage of Chaos Theory
Useful to have a look to things happening in the world different from traditional view
Instead of X-Y graph -> phase-spatial diagrams
Instead of exact position of point -> general condition of system

Usage of Chaos Theory
Simulation of biological systems (most chaotic systems in the world)
Systems of dynamic equations were used for simulating everything from population growth and epidemics to arrhythmic heart beating
Every system could be simulated: stock exchange, even drops falling from the pipe
Fractal archivation claims in future coefficient of compression 600:1
Movie industry couldn’t have realistic landscapes (clouds, rocks, shadows) without technology of fractal graphics

Brownian motion and it’s adaptation
Brownian motion – for example accidental and chaotic motion of dust particles, weighted in water.
Output: frequency diagram
Could be transformed in music
Could be used for landscape creating

Motion of billiard ball
The slightest mistake in angle of first kick will follow to huge disposition after few collisions.
Impossible to predict after 6-7 hits
Only way is to show angle and length to each hit

Motion of billiard ball
Every single loop or dispersion area presents ball behavior
Area of picture, where are results of one experiment is called attraction area.
This self-similarity will last forever, if enlarge picture for long, we’ll still have same forms. => this will be FRACTAL

Fusion of determined fractals
Fractals are predictable.
Fractals are made with aim to predict systems in nature (for example migration of birds)

Tree simulation using Brownian motion and fractal called Pythagor Tree
Order of leaves and branches is complicated and random, BUT can be emulated by short program of 12 rows.
Firstly, we need to generate Pythagor Tree.

Tree simulation using Brownian motion and fractal called Pythagor Tree
On this stage Brownian motion is not used.
Now, every section is the centre of symmetry
Instead of lines are rectangles.
But it still looks like artificial

Tree simulation using Brownian motion and fractal called Pythagor Tree
Now Brownian motion is used to make randomization
Numbers are rounded-up to 2 rank instead of 39

Tree simulation using Brownian motion and fractal called Pythagor Tree
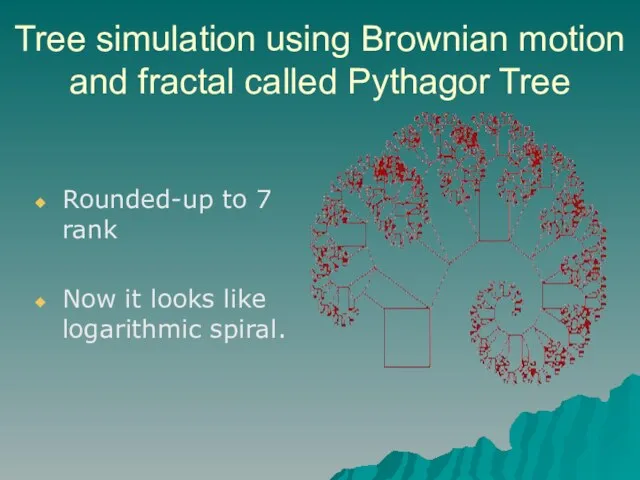
Rounded-up to 7 rank
Now it looks like logarithmic spiral.

Tree simulation using Brownian motion and fractal called Pythagor Tree
To avoid spiral we use Brownian motion twice to the left and only once to the right
Now numbers are rounded-up to 24 rank

Fractals and world around
Branching, leaves on trees, veins in hand, curving river, stock exchange – all these things are fractals.
Programmers and IT specialists go crazy with fractals. Because, in spite of its beauty and complexity, they can be generated with easy formulas.
Discovery of fractals was discovery of new art aesthetics, science and math, and also revolution in humans world perception.

What are fractals in reality?
Fractal – geometric figure definite part of which is repeating changing its size => principle of self-similarity.
There are a lot of types of fractals
Not just complicated figures generated by computers.
Almost everything which seems to be casual could be fractal, even cloud or little molecule of oxygen.

How chaos is chaotic?
Fractals – part of chaos theory.
Chaotic behaviour, so they seem disorderly and casual.
A lot of aspects of self-similarity inside fractal.
Aim of studying fractals and chaos – to predict regularity in systems, which might be absolutely chaotic.
All world around is fractal-like

Geometry of 21st century
Pioneer, father of fractals was Franco-American professor Benoit B. Mandelbrot.
1960 “Fractal geometry of nature”
Purpose was to analyze not smooth and broken forms.
Mandelbrot used word “fractal”, that meant factionalism of these forms
Now Mandelbrot, Clifford A. Pickover, James Gleick, H.O. Peitgen are trying to enlarge area of fractal geometry, so it can be used practical all over the world, from prediction of costs on stock exchange to new discoveries in theoretical physics.

Practical usage of fractals
Computer systems (Fractal archivation, picture compressing without pixelization)
Liquid mechanics
Modulating of turbulent stream
Modulating of tongues of flame
Porous material has fractal structure
Telecommunications (antennas have fractal form)
Surface physics (for description of surface curvature)
Medicine
Biosensor interaction
Heart beating
Biology (description of population model)

Fractal dimension: hidden dimensions
Mandelbrot called not intact dimensions – fractal dimensions (for example 2.76)
Euclid geometry claims that space is straight and flat.
Object which has 3 dimensions correctly is impossible
Examples: Great Britain coastline, human body

Deterministic fractals
First opened fractals.
Self-similarity because of method of generation
Classic fractals, geometric fractals, linear fractals
Creation starts from initiator – basic picture
Process of iteration – adding basic picture to every result

Sierpinskij lattice
Triangles made of interconnection of middle points of large triangle cut from main triangle, generating triangle with large amount of holes.
Initiator – large triangle.
Generator – process of cutting triangles similar to given triangle.
Fractal dimension is 1.584962501

Sierpinskij sponge
Plane fractal cell without square, but with unlimited ties
Would be used as building constructions

Sierpinskij fractal
Don’t mix up this fractal with Sierpinskij lattice.
Initiator and generator are the same.
Fractal dimension is 2.0

Koch Curve
One of the most typical fractals.
Invented by german mathematic Helge fon Koch
Initiator – straight line. Generator – equilateral triangle.
Mandelbrot was making experiments with Koch Curve and had as a result Koch Islands, Koch Crosses, Koch Crystals, and also Koch Curve in 3D
Fractal dimension is 1.261859507

Mandelbrot fractal
Variant of Koch Curve
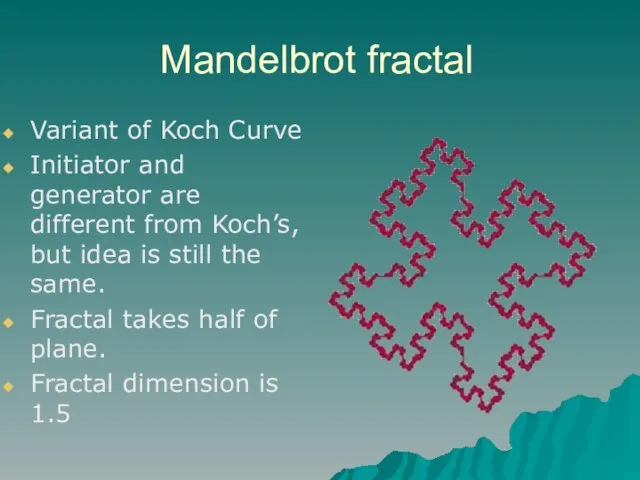
Initiator and generator are different from Koch’s, but idea is still the same.
Fractal takes half of plane.
Fractal dimension is 1.5

Snow Crystal and Star
This objects are classical fractals.
Initiator and generator is one figure

Minkovskij sausage
Inventor is German Minkovskij.
Initiator and generator are quite sophisticated, are made of row of straight corners and segments with different length.
Initiator has 8 parts.
Fractal dimension is 1.5

Labyrinth
Sometimes called H-tree.
Initiator and generator has shape of letter H
To see it easier the H form is not painted in the picture.
Because of changing thickness, dimension on the tip is 2.0, but elements between tips it is changing from 1.333 to 1.6667

Darer pentagon
Pentagon as initiator
Isosceles triangle as generator
Hexagon is a variant of this fractal (David Star)
Fractal dimension is 1.86171

Dragon curve
Invented by Italian mathematic Giuseppe Piano.
Looks like Minkovskij sausage, because has the same generator and easier initiator.
Mandelbrot called it River of Double Dragon.
Fractal dimension is 1.5236

Hilbert curve
Looks like labyrinth, but letter “U” is used and width is not changing.
Fractal dimension is 2.0
Endless iteration could take all plane.

Box
Very simple fractal
Made by adding squares to the top of other squares.
Initiator and generator and squares.
Fractal dimension is 1.892789261

Sophisticated fractals
Most fractals which you can meet in a real life are not deterministic.
Not linear and not compiled from periodic geometrical forms.
Practically even enlarged part of sophisticated fractal is different from initial fractal. They looks the same but not almost identical.

Sophisticated fractals
Are generated by non linear algebraic equations.
Zn+1=ZnІ + C
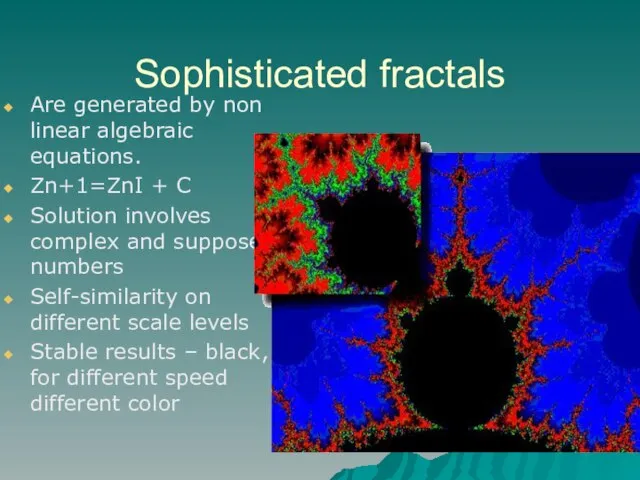
Solution involves complex and supposed numbers
Self-similarity on different scale levels
Stable results – black, for different speed different color

Mandelbrot multitude
Most widespread sophisticated fractal
Zn+1=Zna+C
Z and C – complex numbers
a – any positive number.

Mandelbrot multitude
Z=Z*tg(Z+C).
Because of Tangent function it looks like Apple.
If we switch Cosine it will look like Air Bubbles.
So there are different properties for Mandelbrot multitude.