Фрактал – это голографическая матрица, каждая часть которой отражает Целое. Фракталы могут быть геометрическими, алгебраическими
Содержание
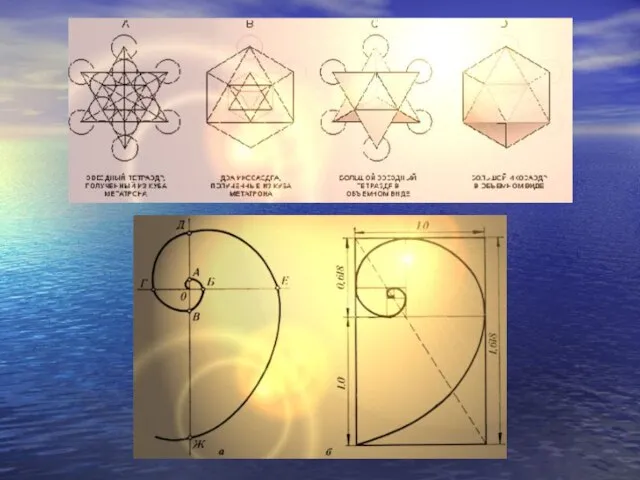
- 2. Золотое сечение Геометрические тела, образующие Вселенную в соответствии с философией Платона Тетраэдр, Куб, Октаэдр, Додекаэдр, Икосаэдр
- 4. Тетраэдр Эта фигура состоит из четырех правильных треугольников. Если эазвернуть их на плоскости, они образуют равносторонний
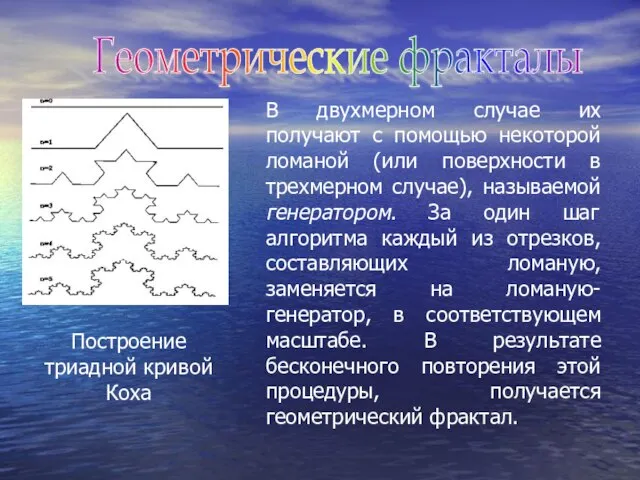
- 5. Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход
- 6. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором.
- 9. Алгебраический фрактал Брокколи
- 10. Капуста Брокколи
- 13. Свойства фракталов Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала
- 14. Алгебраические фракталы получают с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Интерпретируя нелинейный
- 17. ПРЕЗЕНТАЦИЯ разработана и подготовлена творческой группой "ГЕЛИОС" Автор-составитель: Николай Панчишин e-mail: [email protected] м.т. 709-31-27
- 23. Скачать презентацию


















 Стартовая готовность системы образования Челябинской области к внедрению бережливых технологий
Стартовая готовность системы образования Челябинской области к внедрению бережливых технологий Преподавание истории в старших профильных классах как блок-модуль
Преподавание истории в старших профильных классах как блок-модуль f0bc26d9d99bea8f
f0bc26d9d99bea8f Применение теории игр в политике и экономике
Применение теории игр в политике и экономике Отель Амшенский двор
Отель Амшенский двор Типы и возможности ведения переговоров по странам и континентам
Типы и возможности ведения переговоров по странам и континентам Гжель
Гжель Применение игровых технологий для контроля уровня развития двигательных качеств, умений и знаний на уроках гимнастике
Применение игровых технологий для контроля уровня развития двигательных качеств, умений и знаний на уроках гимнастике Автоматизированные рабочие места
Автоматизированные рабочие места Особливості вступной кампаніи та затвердження
Особливості вступной кампаніи та затвердження  Пневматические схемы тепловозов ТЭМ18ДМ, 2М62, 2ТЭ10М
Пневматические схемы тепловозов ТЭМ18ДМ, 2М62, 2ТЭ10М Административные правоотношения
Административные правоотношения Папка проведение ВВ
Папка проведение ВВ Изделия для ландшафтного дизайна
Изделия для ландшафтного дизайна Органоиды клетки
Органоиды клетки Blagotvoritelny_fond_pomoschi_tyazhelobolnym_detyam
Blagotvoritelny_fond_pomoschi_tyazhelobolnym_detyam ОТЧЕ НАШ…
ОТЧЕ НАШ… Многогранники в природе
Многогранники в природе Тауэр в Лондоне
Тауэр в Лондоне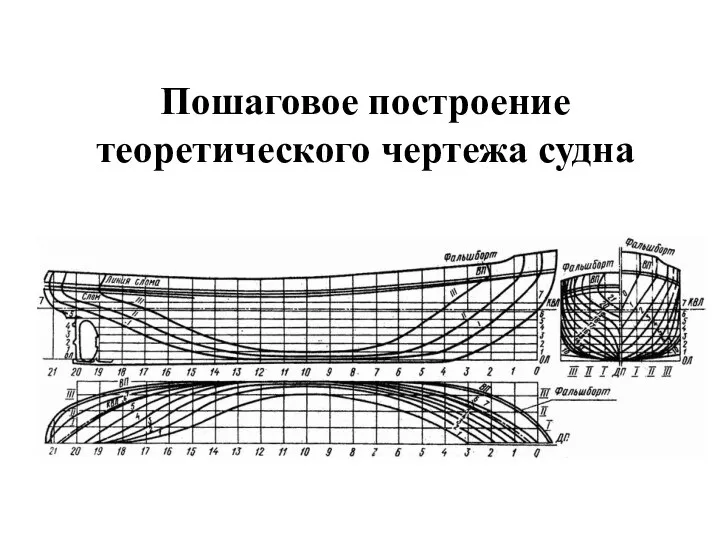 Poshagovoe_postroenie_TCh_sudna (2)
Poshagovoe_postroenie_TCh_sudna (2) Всеукраинский фестиваль инновационных проектов
Всеукраинский фестиваль инновационных проектов Отчет по проделанной работе
Отчет по проделанной работе Расстановка фигур
Расстановка фигур ТЕСТ
ТЕСТ Главные принципы силовой тренировки
Главные принципы силовой тренировки Африканский стиль
Африканский стиль Преза на собру профоргов
Преза на собру профоргов ПЕРЕВОЗКА ДЕНЕГ И ЦЕННОСТЕЙ
ПЕРЕВОЗКА ДЕНЕГ И ЦЕННОСТЕЙ