Содержание
- 2. Рекомендуемая литература Р. Кроновер. Фракталы и хаос в динамических системах. Основы теории: Пер. с англ. Постмаркет,
- 3. Новая философия математики Фрактал — это слово, изобретенное Бенуа Мандельбротом для того, чтобы объединить под одним
- 4. Бенуа Мандельброт
- 5. Б. Мандельброт «Фрактальная геометрия природы» Почему геометрию так часто называют «холодной» и «сухой»? Одна из причин
- 6. Новая геометрия С момента выхода книги Б. Мандельброта «Фрактальная геометрия природы» началось бурное развитие фрактальной геометрии.
- 7. Фракталы в интернете
- 8. Фрактальные картинки
- 9. Береговая линия Норвегии При изучении географии вы, конечно, помните, что каждая из стран имеет свою площадь
- 10. Измерение длины береговой линии Измеренная длина береговой линии как функция длины шага Тот же график в
- 11. А что же все-таки делать с длиной береговой линии? Отказаться ее измерять, потому что она неизмерима?
- 12. Данные собранные Ричардсоном Длина береговых линий как функция выбранного шага δ (км).
- 13. Фрактальная размерность Как объяснить то, что все результаты измерений в дважды логарифмическом масштабе укладываются на прямую?
- 14. Парадокс Шварца Рассмотри равнобедренный прямоугольный треугольник ABC с катетами равными 1. Понятно, что длина кратчайшего пути
- 15. Самоподобие Нередко то, что мы наблюдаем в природе, интригует нас бесконечным повторением одного и то же
- 16. Теорема Пифагора Вот доказательство теоремы Пифагора, предложенное одиннадцатилетним Эйнштейном, и блистательно иллюстрирующее идею самоподобия. Высота, проведенная
- 17. Самоподобие «простых» объектов Разделим отрезок прямой на N равных частей. Тогда каждую часть можно считать копией
- 18. Кривая Коха Кривая, придуманная Гельгом фон Кохом в 1904 году, является фракталом размерности d ≈ 1,2618.
- 19. Свойства кривой Коха Если взять копию K, уменьшенную в три раза (r=3), то все множество K
- 20. Треугольник Серпинского Еще один пример простого самоподобного фрактала — треугольник Серпинского, придуманный польским математиком Вацлавом Серпинским
- 21. Свойства треугольника Серпинского Из построения видно, что весь ковер представляет собой объединение N=3 существенно непересекающихся уменьшенных
- 22. Упражнения 1 Определите размерность подобия фракталов, которые строятся, как указано на рисунках. Вычислите длины и площади.
- 23. L-системы Понятие L-систем, тесно связанное с самоподобными фракталами, появилось в 1968 году благодаря Аристриду Линденмайеру. Изначально
- 24. Команды и интерпретаторы
- 25. Графическая интерпретация Размер шага и величина приращения по углу θ задаются заранее и остаются неизменными для
- 26. Примеры L-систем Снежинка Коха axiom=F++F++F newF=F-F++F-F Θ=π/3 Цветок axiom=F[+F+F][-F-F][++F][--F] newF=FF[++F][+F][F][-F][--F] Θ=π/16 Куст axiom=F newF=-F+F+[+F-F-]-[-F+F+F] Θ=π/8 Остров
- 27. Упражнения 2 Чему равно слово на выходе следующей L-системы после двух итераций: axiom=F; newF=FF-[F]+[F]; Θ=π/4. Изобразите
- 28. Множество Кантора Классическое множество Кантора, или пыль Кантора, названо по имени Георга Кантора, который описал его
- 29. Свойства канторова множества Канторово множество есть самоподобный фрактал размерности d = ln(2)/ln(3) ≈ 0,6309, так как
- 30. Мощность канторова множества Теорема. Мощность множества Кантора С равна мощности континуума [0,1]. Два множества обладают равной
- 31. Упражнения 3 Можно ли утверждать, что каждая точка канторовой пыли является концом какого-то из отрезков, возникающих
- 32. Кривая Пеано Снежинку Коха и другие непрерывные кривые на плоскости, полученные с помощью L-систем, объединяет то,
- 33. Построение кривой Пеано Пусть S — единичный квадрат. Первый шаг построения состоит в том, чтобы разбить
- 34. Теорема. Последовательность непрерывных отображений Pn:[0,1]→S сходится к непрерывному сюръективному отображению P:[0,1]→S, которое называется кривой Пеано. В
- 35. Кривые, заполняющие плоскость
- 36. Упражнения 4 Найдите L-систему, реализующую кривую Пеано. Изобразите, используя компьютерную программу для визуализации L-систем. Найдите образы
- 37. Системы итерированных функций Системы итерированных функций (СИФ) — одно из наиболее замечательных и глубоких достижений в
- 38. План исследования СИФ Для того чтобы дать математически строгое описание СИФ нам понадобятся некоторые базовые понятия
- 39. Метрика Метрикой (расстоянием) на множестве X называется вещественная функция удовлетворяющая следующим аксиомам: d(x, у) ≥ 0
- 40. Теорема о сжимающих отображения Пусть (X,d) — метрическое пространство. Преобразование T : X → X называется
- 41. Метрика Хаусдорфа Одним из основных математических аспектов теории фракталов является вопрос о сходимости некоторой последовательности множеств
- 42. Определение СИФ Пусть (X,d) — полное метрическое пространство. Для чтобы построить систему итерированных функций введем в
- 43. Аттрактор СИФ Теорема. Преобразование T:K→K, определенное соотношением (*), является сжатием на полном метрическом пространстве K. Следовательно,
- 44. Пример Рассмотрим три аффинных преобразования на R2. Несложно проверить, что аттрактором для данной СИФ является треугольник
- 45. Примеры аффинных СИФ
- 46. Примеры аффинных СИФ
- 47. Сжатие изображений Рассмотрим задачу, обратную к нахождению аттрактора СИФ. Пусть в нашем распоряжении имеется некоторое изображение
- 48. Рассмотрим гипотетический пример. Пусть нам требуется передать изображение ковра Серпинского размером 512 х 512. Не применяя
- 49. Теорема коллажа Теорема. Обозначим E0 — исходное изображение; T — сжатие на пространстве непустых компактов, определяемое
- 50. Упражнения 5 Постройте СИФ, аттрактор которой есть в точности квадрат. Используя теорему коллажа, оцените расстояние Хаусдорфа
- 51. Комплексная динамика Вероятно, нельзя привести пример такого компьютерного эксперимента, который впечатлением от результатов превосходил бы то
- 52. Множества Жюлиа Рассмотрим полином одного комплексного переменного Множество Жюлиа функции f, обозначаемое J(f), определяется как Таким
- 53. Множества Жюлиа квадратичных полиномов В первую очередь и в основном, мы будем изучать множества Жюлиа квадратичных
- 54. Упражнения 6 Покажите, что множество Жюлиа произвольного квадратичного полинома g(z)=a2z2+a1z+a0 подобно множеству Жюлиа полинома f(w)=w2+c, где
- 55. Примеры множеств Жюлиа
- 56. Множество Мандельброта Мы уже убедились в том, что множества Жюлиа функции f(z)=z2+c обладают большим разнообразием. Действительно,
- 57. Множество Мандельброта (см. рисунок) M для полинома fс(z)=z2+c определяется как множество всех значений параметра c, для
- 58. Упражнения 7 Покажите, что множество Мандельброта симметрично относительно вещественной оси. Для этого покажите, что отображения топологически
- 59. Проблема Кэли В 1879 году сэр Артур Кэли поставил задачу итерирования комплексных функций, которая позднее стимулировала
- 60. Для f(x)=х3-1 единственный вещественный ноль функции равен 1, и итерации Ньютона принимают вид: Кэли предложил исследовать
- 61. Как и в случае вещественных итераций, если начальная точка z0 находится достаточно близко к корню wk
- 62. Теорема. Границы всех областей притяжения A(wk) совпадают. Теорема говорит нам о том, что ответ на вопрос
- 64. Скачать презентацию
Слайд 2Рекомендуемая литература
Р. Кроновер. Фракталы и хаос в динамических системах. Основы теории: Пер.
Рекомендуемая литература
Р. Кроновер. Фракталы и хаос в динамических системах. Основы теории: Пер.

М. Шредер. Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая: Пер. с англ. НИЦ «Регулярная и хаотическая динамика», Ижевск, 2001.
Е. Федер. Фракталы: Пер. с англ. Мир, М., 1991.
Б. Мандельброт. Фрактальная геометрия природы: Пер. с англ. Институт компьютерных исследований, М., 2002.
M. F. Barnsley. Superfractals. Cambridge University Press, Cambridge, 2006.
Слайд 3Новая философия математики
Фрактал — это слово, изобретенное Бенуа Мандельбротом для того, чтобы
Новая философия математики
Фрактал — это слово, изобретенное Бенуа Мандельбротом для того, чтобы

И тут, как отмечает Мандельброт, Природа сыграла с математиками шутку. Возможно, математикам XIX в. недоставало воображения — Природа же никогда таким недостатком не страдала. Как оказалось, окружающим нас и хорошо знакомым нам объектам всегда были присущи те самые патологические структуры, которые математики изобрели, чтобы избавиться от уз натурализма XIX в.
Слайд 4Бенуа Мандельброт
Бенуа Мандельброт

Слайд 5Б. Мандельброт
«Фрактальная геометрия природы»
Почему геометрию так часто называют «холодной» и
Б. Мандельброт
«Фрактальная геометрия природы»
Почему геометрию так часто называют «холодной» и

В более общем виде я заявляю, что многие формы Природы настолько неправильны и фрагментированы, что в сравнении с евклидовыми фигурами Природа демонстрирует не просто более высокую степень, но совершенно иной уровень сложности. Количество различных масштабов длины в естественных формах можно считать бесконечным для каких угодно практических задач.
Существование таких феноменов бросает нам вызов и побуждает заняться подробным изучением тех из форм, которые Евклид отложил в сторону из-за их «бесформенности» — исследовать, так сказать, морфологию «аморфного». Математики же пренебрегли этим вызовом и предпочли бежать от природы путем изобретения всевозможных теорий, которые никак не объясняют того, что мы видим или ощущаем.
Рискнув ответить на вызов, я задумал и разработал новую геометрию Природы, а также нашел для нее применение во многих разнообразных областях. Новая геометрия способна описать многие из неправильных и фрагментированных форм в окружающем нас мире и породить вполне законченные теории, определив семейство фигур, которые я называю фракталами.
Слайд 6Новая геометрия
С момента выхода книги Б. Мандельброта «Фрактальная геометрия природы» началось бурное
Новая геометрия
С момента выхода книги Б. Мандельброта «Фрактальная геометрия природы» началось бурное

Всем этим человечество обязано математику Бенуа Мандельброту. То, что новую науку со столь широкими приложениями создал один человек, выглядит невероятным. В наше время все значительные достижения науки и технологий являются плодами работы коллективов. Время одиночек–энциклопедистов прошло, специализация достигла такой степени, что одному человеку не под силу охватить даже основные идеи из разных областей. Для этого надо быть гением. Но многие так и считают: открыв фракталы, Б. Мандельброт совершил переворот в физике, утверждают авторы книги «От Ньютона до Мандельброта» (Штауффер Д., Стэнли Х.Е.).
Слайд 7Фракталы в интернете
Фракталы в интернете
Слайд 8Фрактальные картинки
Фрактальные картинки
Слайд 9Береговая линия Норвегии
При изучении географии вы, конечно, помните, что каждая из стран
Береговая линия Норвегии
При изучении географии вы, конечно, помните, что каждая из стран

Мы можем измерить длину береговой линии только приблизительно. По мере того как мы уменьшаем масштаб, нам приходится измерять все больше маленьких мысов и бухт — длина береговой линии увеличивается, и объективного предела уменьшению масштаба (и, тем самым, увеличению длины береговой линии) просто не существует; мы вынуждены признать, что эта линия имеет бесконечную длину.
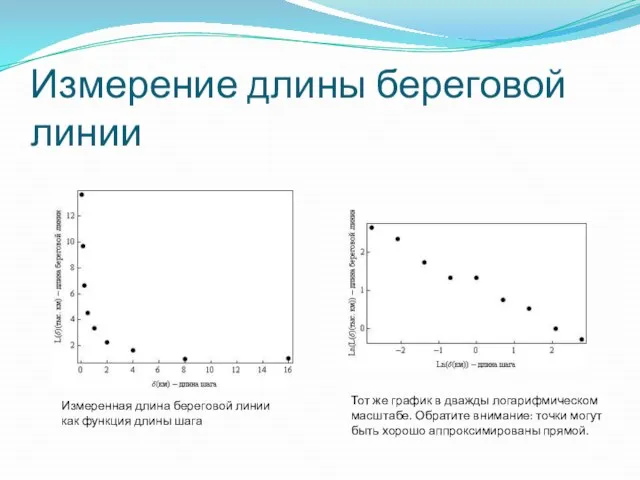
Слайд 10Измерение длины береговой линии
Измеренная длина береговой линии как функция длины шага
Тот
Измерение длины береговой линии
Измеренная длина береговой линии как функция длины шага
Тот
Слайд 11А что же все-таки делать с длиной береговой линии? Отказаться ее измерять,
А что же все-таки делать с длиной береговой линии? Отказаться ее измерять,

Нет, это не выход. Просто, приводя длину береговой линии, следует всегда указывать, по картам какого масштаба она измерялась, каким способом. Без указания масштаба карт всякие данные о длине береговой линии теряют смысл. К сожалению, даже в источниках, претендующих на сугубую солидность, можно встретить страшные нелепости. Например, известный сайт ЦРУ «The World Factbook». Здесь для каждой страны и океана приведены данные по береговой линии, но способ измерения не указан. В результате береговая линия Канады оказывается больше 200 тыс. км, Северного Ледовитого океана — 45,4 тыс. км, Атлантического — 111,9 тыс. км (данные приведены с точностью до километра). Береговая линия двух из трех океанов, омывающих Канаду, в сумме меньше береговой линии одной только Канады. Для Норвегии приведена цифра 21 925 км и дано примечание: «Материк 3419 км, большие острова 2413 км, длинные фьорды, многочисленные маленькие острова и мелкие изгибы (в буквальном переводе зазубрины) береговой линии 16 093 км». В сумме получается как раз указанная общая длина береговой линии. Но вот почему берега фьордов — не часть береговой линии материка, почему длина зазубрин приплюсована к длине береговой линии материка, какие острова считать большими — обо всем этом приходится только догадываться. Совершенно бесспорные данные в этой таблице приведены только для Андорры, Австрии, Ботсваны, Венгрии, Свазиленда и подобных им стран, выхода к морю не имеющих, — написано: «0 км».
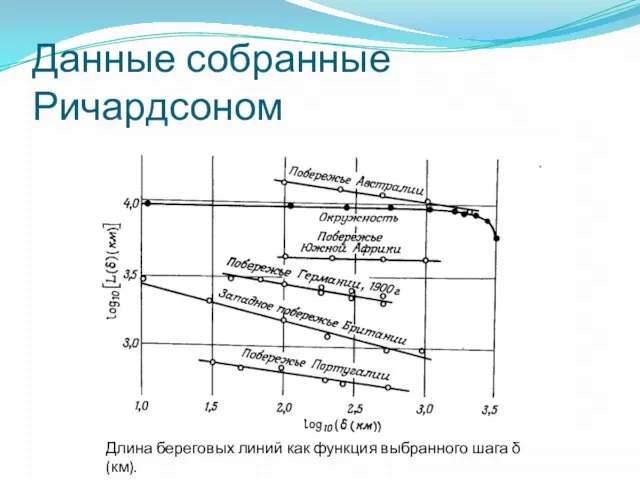
Слайд 12Данные собранные Ричардсоном
Длина береговых линий как функция выбранного шага δ (км).
Данные собранные Ричардсоном
Длина береговых линий как функция выбранного шага δ (км).
Слайд 13Фрактальная размерность
Как объяснить то, что все результаты измерений в дважды логарифмическом масштабе
Фрактальная размерность
Как объяснить то, что все результаты измерений в дважды логарифмическом масштабе

Имеем
где a и b — некоторые константы. Потенцируя, получим
С одной стороны, константа b есть тангенс угла наклона прямой, причем, как следует из графиков, она не положительна. С другой стороны она имеет важный физический смысл — чем она больше по модулю, тем быстрее растет длина побережья с уменьшением длины шага, и, следовательно, более изрезанным выглядит побережье. В дальнейшем мы увидим, что константа b тесно связана с одной из важнейших характеристик фрактальных кривых — фрактальной размерностью.
Слайд 14Парадокс Шварца
Рассмотри равнобедренный прямоугольный треугольник ABC с катетами равными 1. Понятно, что
Парадокс Шварца
Рассмотри равнобедренный прямоугольный треугольник ABC с катетами равными 1. Понятно, что

Слайд 15Самоподобие
Нередко то, что мы наблюдаем в природе, интригует нас бесконечным повторением одного
Самоподобие
Нередко то, что мы наблюдаем в природе, интригует нас бесконечным повторением одного

Многие законы природы не зависят (или почти не зависят) от масштаба. То, что скейлинг (изменение масштаба) обычно имеет предел (постоянную Планка — когда объекты становятся слишком малыми, или скорость света — когда объекты движутся слишком быстро), не умаляет полезности «размышлений в терминах самоподобия» — так это не создает сколь-нибудь серьезных препятствий для применения этого понятия в реальном мире. Так, в турбулентных потоках крупные вихри порождают меньшие, те, в свою очередь, — еще меньшие и так почти до бесконечности.
Слайд 16Теорема Пифагора
Вот доказательство теоремы Пифагора, предложенное одиннадцатилетним Эйнштейном, и блистательно иллюстрирующее идею
Теорема Пифагора
Вот доказательство теоремы Пифагора, предложенное одиннадцатилетним Эйнштейном, и блистательно иллюстрирующее идею

Высота, проведенная из прямого угла, делит большой треугольник на два меньших, подобных друг другу и большому треугольнику. Учитывая, что площади подобных фигур относятся как квадраты соответствующих линейных размеров, получим соотношение для площадей
где k — некоторый отличный от нуля множитель, один и тот же во всех трех соотношениях. Учитывая, что
получим
Слайд 17Самоподобие «простых» объектов
Разделим отрезок прямой на N равных частей. Тогда каждую часть
Самоподобие «простых» объектов
Разделим отрезок прямой на N равных частей. Тогда каждую часть

Рассмотренные множества обладают целой размерностью. Зададимся вопросом, возможно ли такое построение, при котором показатель d не является целым, то есть такое, что при разбиении исходного множества на N непересекающихся подмножеств, полученных масштабированием оригинала с коэффициентом r значение d не будет выражаться целым числом. Ответ, как мы убедимся — решительное да! Такое множество называют самоподобным фракталом. Величину d называют фрактальной (дробной) размерностью или размерностью подобия.
Слайд 18Кривая Коха
Кривая, придуманная Гельгом фон Кохом в 1904 году, является фракталом размерности
Кривая Коха
Кривая, придуманная Гельгом фон Кохом в 1904 году, является фракталом размерности

Пусть K0 — начальный отрезок. Уберем среднюю треть и добавим два новых отрезка такой же длины, как показано на рисунке. Назовем полученное множество К1. Повторим данную процедуру многократно, на каждом шаге заменяя среднюю треть двумя новыми отрезками. Обозначим через Kn фигуру, полу- получившуюся после n-го шага. Интуитивно ясно, что последовательность кривых {Kn} сходится к некоторой предельной кривой K. Мы проведем строгое математическое исследование сходимости таких последовательностей кривых и других позже. Пока что предположим, что кривая K существует, и рассмотрим некоторые ее свойства.
Слайд 19Свойства кривой Коха
Если взять копию K, уменьшенную в три раза (r=3), то
Свойства кривой Коха
Если взять копию K, уменьшенную в три раза (r=3), то

Еще одно важное свойство кривой Коха — ее бесконечная длина. Пусть исходный отрезок K0 имеет единичную длину. Тогда длина кривой K1 равна 4/3. Длина кривой K2 равна 16/9. Продолжая таким образом имеем, что кривая Kn после n-го шага имеет длину 4n/3n. Следовательно, длина предельной кривой K равна бесконечности:
Тот же факт можно доказать с использованием идеи самоподобия. Очевидно, что кривая K состоит из четырех кусков каждый из которых в три раза меньше самой кривой. Следовательно, если бы кривая K имела конечную длину, скажем L>0, то должно было бы выполняться соотношение
откуда следует, что L=∞.
Слайд 20Треугольник Серпинского
Еще один пример простого самоподобного фрактала — треугольник Серпинского, придуманный польским
Треугольник Серпинского
Еще один пример простого самоподобного фрактала — треугольник Серпинского, придуманный польским

Пусть начальное множество S0 — равносторонний треугольник вместе с областью, которую он замыкает. Разобьем S0 на четыре меньшие треугольные области, соединив отрезками середины сторон исходного треугольника. Удалим внутренность маленькой центральной треугольной области. Назовем оставшееся множество S1. Затем повторим процесс для каждого из трех оставшихся маленьких треугольников и получим следующее приближение S2. Продолжая таким образом, получим последовательность вложенных множеств Sn, чье пересечение и образует ковер S.
Слайд 21Свойства треугольника Серпинского
Из построения видно, что весь ковер представляет собой объединение N=3
Свойства треугольника Серпинского
Из построения видно, что весь ковер представляет собой объединение N=3

Очевидно, что суммарная площадь частей, выкинутых при построении, в точности равна площади исходного треугольника. На первом шаге мы выбросили 1/4 часть площади. На следующем шаге мы выбросили три треугольника, причем площадь каждого равна 1/16 площади исходного. Рассуждая таким образом, мы убеждаемся, что полная доля выкинутой площади составила:
Следовательно, мы можем утверждать, что оставшееся множество S имеет нулевую площадь.
Слайд 22Упражнения 1
Определите размерность подобия фракталов, которые строятся, как указано на рисунках. Вычислите
Упражнения 1
Определите размерность подобия фракталов, которые строятся, как указано на рисунках. Вычислите

Постройте самоподобное множество размерности 1, отличное от отрезка.
(а)
(б)
(в)
(г)
(д)
(е)
(ж)
Слайд 23L-системы
Понятие L-систем, тесно связанное с самоподобными фракталами, появилось в 1968 году благодаря
L-системы
Понятие L-систем, тесно связанное с самоподобными фракталами, появилось в 1968 году благодаря

Для графической реализации L-систем в качестве подсистемы вывода используется так называемая тертл-графика (turtle — черепаха). При этом точка (черепашка) движется по экрану дискретными шагами, как правило, прочерчивая свой след, но при необходимости может перемещаться без рисования. В нашем распоряжении имеются три параметра (x,y,α), где (х,у) — координаты черепашки, α — направление, в котором она смотрит. Черепашка обучена интерпретировать и выполнять последовательность команд, задаваемых кодовым словом, буквы которого читаются слева направо. Кодовое слово представляет собой результат работы L-системы и может включать следующие команды и интерпретаторы:
Слайд 24Команды и интерпретаторы
Команды и интерпретаторы

Слайд 25Графическая интерпретация
Размер шага и величина приращения по углу θ задаются заранее и
Графическая интерпретация
Размер шага и величина приращения по углу θ задаются заранее и

Формально, L-система состоит из алфавита, слова инициализации, называемого аксиомой или инициатором, и набора порождающих правил, указывающих, как следует преобразовывать слово при переходе от уровня к уровню (от итерации к итерации). К примеру, можно заменять букву F при помощи порождающего правила newf = F-F++F-F, что соответствует L-системе для кривой Коха. Остальные символы не обновляются, а просто остаются на тех местах, где они встретились. Обновление букв в данном слове предполагается одновременным, то есть все буквы слова одного уровня обновляются раньше любой буквы следующего уровня.
L-система, соответствующая кривой Коха, задается следующим образом:
θ = π/3;
аксиома: axiom=F;
порождающее правило: newF = F+F--F+F.
Графическое представление аксиомы F — отрезок. На первом шаге каждая буква F в слове—инициаторе заменяется на F+F--F+F. Графическое представление — в точности первый шаг построения кривой Коха. Повторяя этот процесс, на втором шаге получим:
F+F--F+F+F+F--F+F--F+F--F+F+F+F--F+F.
Несложно заметить, что графическая реализация есть второй шаг построения кривой Коха и т.д.
Следующая программа предназначена для графической реализации L-систем.
Слайд 26Примеры L-систем
Снежинка Коха
axiom=F++F++F
newF=F-F++F-F
Θ=π/3
Цветок
axiom=F[+F+F][-F-F][++F][--F]
newF=FF[++F][+F][F][-F][--F]
Θ=π/16
Куст
axiom=F
newF=-F+F+[+F-F-]-[-F+F+F]
Θ=π/8
Остров
axiom=F+F+F+F
newF=F+F-F-FFF+F+F-F
Θ=π/2
Снежинка
axiom=[F]+[F]+[F]+[F]+[F]+[F]
newF=F[++F][-FF]FF[+F][-F]FF
Θ=π/3
Сорняк
axiom=F
newF=F[+F]F[-F]F
Θ=π/7
Примеры L-систем
Снежинка Коха
axiom=F++F++F
newF=F-F++F-F
Θ=π/3
Цветок
axiom=F[+F+F][-F-F][++F][--F]
newF=FF[++F][+F][F][-F][--F]
Θ=π/16
Куст
axiom=F
newF=-F+F+[+F-F-]-[-F+F+F]
Θ=π/8
Остров
axiom=F+F+F+F
newF=F+F-F-FFF+F+F-F
Θ=π/2
Снежинка
axiom=[F]+[F]+[F]+[F]+[F]+[F]
newF=F[++F][-FF]FF[+F][-F]FF
Θ=π/3
Сорняк
axiom=F
newF=F[+F]F[-F]F
Θ=π/7
![Примеры L-систем Снежинка Коха axiom=F++F++F newF=F-F++F-F Θ=π/3 Цветок axiom=F[+F+F][-F-F][++F][--F] newF=FF[++F][+F][F][-F][--F] Θ=π/16 Куст](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/428006/slide-25.jpg)
Слайд 27Упражнения 2
Чему равно слово на выходе следующей L-системы после двух итераций:
axiom=F;
newF=FF-[F]+[F];
Θ=π/4.
Изобразите
Упражнения 2
Чему равно слово на выходе следующей L-системы после двух итераций:
axiom=F;
newF=FF-[F]+[F];
Θ=π/4.
Изобразите

Напишите псевдокод для L-систем, реализующих правила на рисунках (а) и (б) (положить axiom = F).
Постройте L-системы для фракталов из упражнения 1 пункты (a) – (д). Отобразите результат работы L-систем в графике.
Придумайте и реализуйте на компьютере три новые L-системы, результатом работы которых были бы ваши собственные варианты следующих фигур: снежинка, остров (с границей без разрывов), куст или сорняк.
(а)
(б)
Слайд 28Множество Кантора
Классическое множество Кантора, или пыль Кантора, названо по имени Георга Кантора,
Множество Кантора
Классическое множество Кантора, или пыль Кантора, названо по имени Георга Кантора,

Построение классической пыли Кантора начинается с выбрасывания средней трети (не включая концы) единичного отрезка. То есть исходное множество есть отрезок [0,1], и первый шаг состоит в удалении открытого интервала [1/3,2/3]. На следующем и всех остальных шагах мы выкидываем среднюю треть (не включая концы) всех отрезков текущего уровня. Таким образом, мы получаем убывающую последовательность множеств:
Предельное множество C, которое представляет собой пересечение множеств {Cn}, называется классическим канторовым множеством.
Слайд 29Свойства канторова множества
Канторово множество есть самоподобный фрактал размерности d = ln(2)/ln(3) ≈
Свойства канторова множества
Канторово множество есть самоподобный фрактал размерности d = ln(2)/ln(3) ≈

Канторово множество не содержит интервалов положительной длины. Это очевидно из построения.
Сумма длин интервалов, удаленных при построении множества C, в точности равна 1. Доказательство аналогично тому, что было проведено при вычислении площади треугольника Серпинского.
Классическое канторово множество представляет собой пример компактного, совершенного и вполне разрывного множества. Более того, можно утверждать, что топологически классическое множество Кантора определяется как компактное, совершенное и вполне разрывное множество. Это означает, что любое компактное, совершенное и вполне разрывное множество гомеоморфно канторову множеству.
Слайд 30Мощность канторова множества
Теорема. Мощность множества Кантора С равна мощности континуума [0,1].
Два
Мощность канторова множества
Теорема. Мощность множества Кантора С равна мощности континуума [0,1].
Два
![Мощность канторова множества Теорема. Мощность множества Кантора С равна мощности континуума [0,1].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/428006/slide-29.jpg)
Таким образом, нам необходимо установить взаимно однозначное соответствие между точками из С и точками отрезка [0,1]. Для этого нам потребуется рассмотреть двоичное (по основанию 2), а также троичное (по основанию 3) представления точек отрезка [0,1].
Для того чтобы избежать двусмысленности в случае, когда точка имеет два двоичных или троичных представления, мы будем всегда выбирать то представление, которое заканчивается всеми нулями в двоичном или в троичном представлениях.
Заметим, что точка попадает в множество Кантора С тогда и только тогда, когда в ее троичном представлении отсутствуют единицы, то есть когда в нем присутствуют только нули и двойки. Тогда искомое соответствие точек из С с точками отрезка [0,1] осуществляется заменой всех двоек в троичном представлении x на единицы. Полученное таким образом двоичное представление определяет некоторое вещественное число y. Например, если x=0,220200020… (в троичной системе), то полагаем y=0,110100010… (в двоичной системе). Описанная процедура определяет взаимно однозначное соответствие между точками x из C и y из [0,1].
Слайд 31Упражнения 3
Можно ли утверждать, что каждая точка канторовой пыли является концом какого-то
Упражнения 3
Можно ли утверждать, что каждая точка канторовой пыли является концом какого-то

Является ли треугольник Серпинского множеством Кантора? Обосновать ответ.
Определите фрактальную размерность (размерность подобия) модифицированного множества Кантора, в котором на каждом шаге выбрасывается центральная пятая часть каждого интервала.
Определите размерность фрактала, состоящего из таких точек отрезка [0,1], в десятиричном представлении которых x=0,x0x1x2… отсутствуют цифры 3 и 7.
Определите размерность фрактала на плоскости, состоящего из точек единичного квадрата (х, у), причем в системе счисления с основанием 5 в записи числа x=0,x0x1x2… отсутствуют цифры 2 и 4, а в записи числа y=0,y0y1y2… отсутствуют цифры 0, 1 и 3. Изобразить полученное множество.
Слайд 32Кривая Пеано
Снежинку Коха и другие непрерывные кривые на плоскости, полученные с помощью
Кривая Пеано
Снежинку Коха и другие непрерывные кривые на плоскости, полученные с помощью

Слайд 33Построение кривой Пеано
Пусть S — единичный квадрат. Первый шаг построения состоит в
Построение кривой Пеано
Пусть S — единичный квадрат. Первый шаг построения состоит в

Далее, каждый из этих девяти квадратов разбивается на девять равных подквадратов, которые нумеруются аналогично тому, как это было сделано на первой итерации. Получаем кривую P2:[0,1]→S, которая проходит через девять подквадратов таким образом, что ее начальная и конечная точки ложатся на кривую предыдущего уровня. Это позволяет нам занумеровать подквадраты числами от 0 до 8 внутри каждого квадрата (рис. (б)).
Повторим описанную процедуру бесконечно, каждый раз разбивая квадраты на девять подквадратов, строя кривую через все подквадраты так, чтобы ее концы ложились на линию предыдущего уровня, и занумеровывая их.
(а)
(б)
Слайд 34Теорема. Последовательность непрерывных отображений Pn:[0,1]→S сходится к непрерывному сюръективному отображению P:[0,1]→S, которое
Теорема. Последовательность непрерывных отображений Pn:[0,1]→S сходится к непрерывному сюръективному отображению P:[0,1]→S, которое
![Теорема. Последовательность непрерывных отображений Pn:[0,1]→S сходится к непрерывному сюръективному отображению P:[0,1]→S, которое](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/428006/slide-33.jpg)
В процессе построения отображений Pn мы разбивали единичный квадрат S на все более мелкие квадраты и нумеровали их. Таким образом, каждой точке A из S соответствует некоторая (возможно не единственная) бесконечная последовательность цифр от 0 до 8: A↔x1x2x3…
Из построения очевидно, что если x=0,x1x2x3… — девятичное представление точки x из единичного отрезка, то P1(x) принадлежит подквадрату первого уровня с номером x1, P2(x) принадлежит подквадрату второго уровня с номером x2 и т.д. Таким образом, Pn(x) сходится к точке пересечения вложенных подквадратов с номерами x1x2x3… Это доказывает сюръективность отображения Пеано.
Чтобы доказать непрерывность отображения P, достаточно заметить, что сходимость Pn→P равномерная, следовательно, по теореме о равномерной сходимости из стандартного курса математического анализа, предельное отображение также непрерывно.
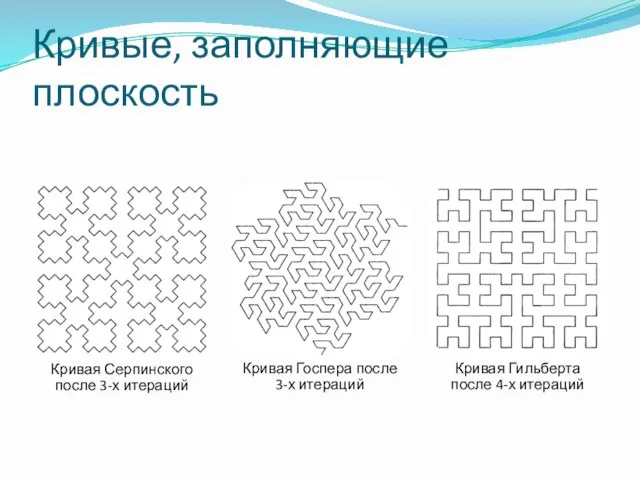
Слайд 35Кривые, заполняющие плоскость
Кривые, заполняющие плоскость
Слайд 36Упражнения 4
Найдите L-систему, реализующую кривую Пеано. Изобразите, используя компьютерную программу для визуализации
Упражнения 4
Найдите L-систему, реализующую кривую Пеано. Изобразите, используя компьютерную программу для визуализации

Найдите образы точек x=0,4444…, y=0,2222… (в девятиричной системе) при отображении Пеано.
Найдите четыре представления Пеано для точек (1/3,7/9) и (2/3,7/9).
Определите все точки единичного квадрата, представление Пеано которых единственно. Какие точки имеют два различных представления? Какие точки имеют четыре различных представления?
Найдите геометрическое место точек единичного квадрата, в представлении Пеано которых отсутствует цифра 5. Является ли это множество фракталом? Если да, то какова его размерность?
Найдите L-системы, реализующие кривые Гильберта, Госпера и Серпинского. Изобразите, используя программу для визуализации L-систем.
Слайд 37Системы итерированных функций
Системы итерированных функций (СИФ) — одно из наиболее замечательных и
Системы итерированных функций
Системы итерированных функций (СИФ) — одно из наиболее замечательных и

Следует иметь в виду с самого начала, что результат применения СИФ, называемый аттрактором, не всегда является фракталом. Это может быть любой компакт, включая интервал или квадрат. Тем не менее, изучение СИФ важно для фрактальной теории, так как с их помощью можно получить удивительное множество фракталов.
Слайд 38План исследования СИФ
Для того чтобы дать математически строгое описание СИФ нам понадобятся
План исследования СИФ
Для того чтобы дать математически строгое описание СИФ нам понадобятся

Определение метрики и метрического пространства.
Формулировка теоремы о сжимающих отображениях.
Определение метрики Хаусдорфа на множестве непустых компактов.
Определение СИФ.
Определение аттрактора СИФ.
Примеры аттракторов.
Упражнения.
Слайд 39Метрика
Метрикой (расстоянием) на множестве X называется вещественная функция
удовлетворяющая следующим аксиомам:
d(x,
Метрика
Метрикой (расстоянием) на множестве X называется вещественная функция
удовлетворяющая следующим аксиомам:
d(x,

d(x, у) = 0 тогда и только тогда, когда х = у.
d(x, у) = d(y, x).
d(x, z) ≤ d(x, y) + d(y, z) для всех х, у, z из X.
Метрическим пространством называется пара (X,d).
Метрическое пространство (X,d) называется полным, если любая последовательность Коши из X сходится к некоторой точке из X.
Слайд 40Теорема о сжимающих отображения
Пусть (X,d) — метрическое пространство. Преобразование T : X
Теорема о сжимающих отображения
Пусть (X,d) — метрическое пространство. Преобразование T : X

для любых x, y из X. Число s называется коэффициентом сжатия.
Теорема. Пусть (X,d) — полное метрическое пространство и T : X → X — сжимающее отображение. Тогда T имеет в точности одну неподвижную точку, то есть существует такая точка x* из X, что T(x*) = x*. Кроме того, для любой начальной точки x
Иными словами, орбита любой точки x0=x, x1=T(x0), x2=T(x1), x3=T(x2) … сходится к x*.
Слайд 41Метрика Хаусдорфа
Одним из основных математических аспектов теории фракталов является вопрос о сходимости
Метрика Хаусдорфа
Одним из основных математических аспектов теории фракталов является вопрос о сходимости

Метрика Хаусдорфа определяется на множестве K всех непустых компактных подмножеств полного метрического пространства (X,d) (как правило, в качестве X выступает евклидово пространство Rn). Таким образом, «точки» из K суть компактные множества из X.
Пусть E — непустой компакт из (X,d) и ε ≥ 0. Тогда ε-оболочкой множества E называется множество
Расстоянием по Хаусдорфу между двумя непустыми компактами E и F будем называть следующую величину:
Известно, что множество K, снабженное метрикой dH, является полным метрическим пространством.
Слайд 42Определение СИФ
Пусть (X,d) — полное метрическое пространство. Для чтобы построить систему итерированных
Определение СИФ
Пусть (X,d) — полное метрическое пространство. Для чтобы построить систему итерированных

Эти m отображений используются для построения одного сжимающего отображения на пространстве K всех непустых компактов из X
Это преобразование ставит в соответствие «точкам» из K, также «точки» из K, причем под точками здесь понимаются компактные множества.
Таким образом, системой итерированных функций называют совокупность введенных выше отображений Tj вместе с индуцированным ими отображением T, действующим на K.
Слайд 43Аттрактор СИФ
Теорема. Преобразование T:K→K, определенное соотношением (*), является сжатием на полном метрическом
Аттрактор СИФ
Теорема. Преобразование T:K→K, определенное соотношением (*), является сжатием на полном метрическом

Следовательно, по теореме о сжимающих отображениях T обладает единственной неподвижной точкой E* из K, т.е T(E*)=E*. Это непустое компактное множество E*, мы будем называть аттрактором СИФ. Аттрактор часто (но не всегда!) оказывается фрактальным множеством.
Теорема о сжимающих отображениях позволяет с высокой точностью получать изображение аттрактора на экране компьютера. Начиная с произвольного (возможно одноточечного) множества E0 , мы находим орбиту этого множества при действии трансформации T, т.е. E0 , E1=T(E0), E2=T(E1), … . Из теоремы о сжимающих отображениях следует, что орбита сходится к аттрактору E*. Таким образом, мы можем построить множество En сколь угодно близкое к E*.
Слайд 44Пример
Рассмотрим три аффинных преобразования на R2.
Несложно проверить, что аттрактором для данной СИФ
Пример
Рассмотрим три аффинных преобразования на R2.
Несложно проверить, что аттрактором для данной СИФ

Следующая программа позволяет строить аттракторы СИФ, состоящих из аффинных преобразований.
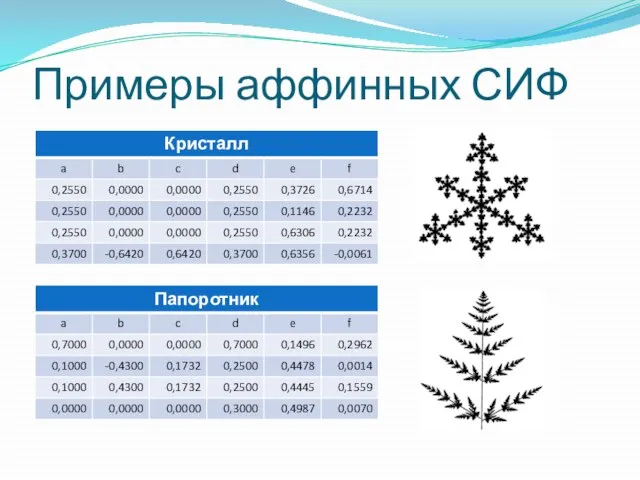
Слайд 45Примеры аффинных СИФ
Примеры аффинных СИФ
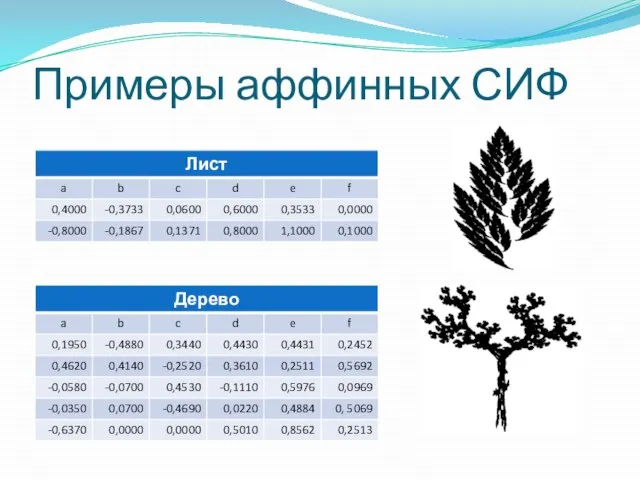
Слайд 46Примеры аффинных СИФ
Примеры аффинных СИФ
Слайд 47Сжатие изображений
Рассмотрим задачу, обратную к нахождению аттрактора СИФ. Пусть в нашем распоряжении
Сжатие изображений
Рассмотрим задачу, обратную к нахождению аттрактора СИФ. Пусть в нашем распоряжении

Один привлекательный способ сжатия изображения заключается в том, чтобы разбить исходное изображение на компоненты и считать их аттракторами некоторых СИФ. Так как каждое аффинное преобразование определяется всего лишь шестью коэффициентами, то полное изображение, в принципе, может быть закодировано достаточно малым числом аффинных коэффициентов. Тогда по кабелю можно передавать коэффициенты, а изображение (совокупность аттракторов) восстанавливать по ним, выполняя алгоритм СИФ.
Слайд 48Рассмотрим гипотетический пример. Пусть нам требуется передать изображение ковра Серпинского размером 512
Рассмотрим гипотетический пример. Пусть нам требуется передать изображение ковра Серпинского размером 512

Оставляя на время в стороне вопрос об отыскании аффинных отображений для аттрактора, соответствующего исходному изображению, обратимся к главному математическому аспекту проблемы. Следующая теорема, называемая теоремой коллажа, позволяет оценить расстояние между исходным и восстановленным изображениями без непосредственного восстановления, что существенно сокращает объем вычислений, необходимых для оценки качества восстановления.
Восстановление изображений
Слайд 49Теорема коллажа
Теорема. Обозначим E0 — исходное изображение; T — сжатие на пространстве
Теорема коллажа
Теорема. Обозначим E0 — исходное изображение; T — сжатие на пространстве

Многократно применяя неравенство треугольника, получим
Слайд 50Упражнения 5
Постройте СИФ, аттрактор которой есть в точности квадрат.
Используя теорему коллажа,
Упражнения 5
Постройте СИФ, аттрактор которой есть в точности квадрат.
Используя теорему коллажа,
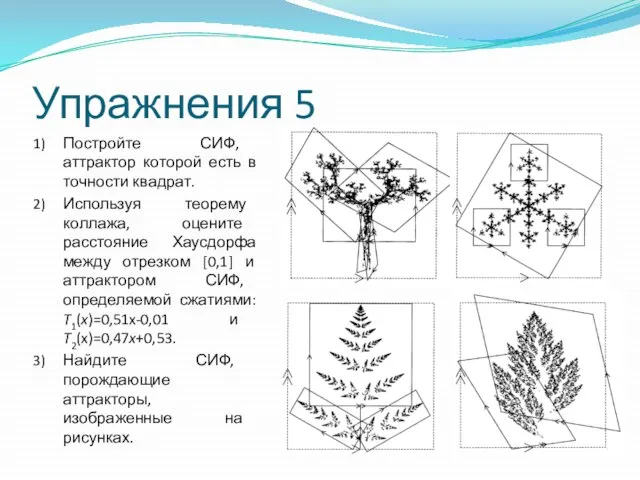
Найдите СИФ, порождающие аттракторы, изображенные на рисунках.
Слайд 51Комплексная динамика
Вероятно, нельзя привести пример такого компьютерного эксперимента, который впечатлением от результатов
Комплексная динамика
Вероятно, нельзя привести пример такого компьютерного эксперимента, который впечатлением от результатов

Множество Жюлиа названо в честь французского математика Гастона Жюлиа (1893-1978), который одновременно с Пьером Фату (1878-1929) в 1917-1919гг. написал основополагающие статьи по итерированию функций комплексного переменного. Еще раз мы видим впечатляющий пример математических исследований, которые далеко опередили свое время в том смысле, что потребовалось более пятидесяти лет, прежде чем компьютерная графика достигла уровня, позволяющего наблюдать эти математические объекты.
Слайд 52Множества Жюлиа
Рассмотрим полином одного комплексного переменного
Множество Жюлиа функции f, обозначаемое J(f), определяется
Множества Жюлиа
Рассмотрим полином одного комплексного переменного
Множество Жюлиа функции f, обозначаемое J(f), определяется

Таким образом, множество Жюлиа функции f есть граница множества точек z, стремящихся к бесконечности при итерировании f(z).
Наряду с множеством Жюлиа часто рассматривают и заполняющее множество Жюлиа, состоящее из точек, орбиты которых ограничены, в отличие от границы этого множества, которое и является настоящим множеством Жюлиа. Заполняющие множества более привлекательны визуально и именно по этой причине наиболее часто реализуются программно.
Слайд 53Множества Жюлиа квадратичных полиномов
В первую очередь и в основном, мы будем изучать
Множества Жюлиа квадратичных полиномов
В первую очередь и в основном, мы будем изучать

где c — комплексная константа. Такой подход не является ограниченным, как это может показаться, так как рассмотрение произвольного квадратичного полинома может быть сведено к указанному выше частному случаю простой заменой переменных (см. упр. 7).
Простейшее множество Жюлиа соответствует случаю f(z)=z2. Несложно заметить, что f n(z)→∞ тогда и только тогда, когда |z| > 1. Границей этого множества, то есть множеством Жюлиа, является единичная окружность {z : |z| = 1}, которая фракталом не является, хотя в общем случае множество Жюлиа есть фрактал.
Следующая программа позволяет строить множества Жюлиа.
Слайд 54Упражнения 6
Покажите, что множество Жюлиа произвольного квадратичного полинома g(z)=a2z2+a1z+a0 подобно множеству Жюлиа
Упражнения 6
Покажите, что множество Жюлиа произвольного квадратичного полинома g(z)=a2z2+a1z+a0 подобно множеству Жюлиа

где T(z)=a2z+a1.
Используя программу, постройте множества Жюлиа следующих квадратичных полиномов: f(z)=z2-1, f(z)=z2-0.2+0.75i, f(z)=z2-0.1244+0.7560i, f(z)=z2-0.1194+0.6289i. Сравните результаты с множествами Жюлиа, изображенными на рисунках.
Слайд 55Примеры множеств Жюлиа
Примеры множеств Жюлиа

Слайд 56Множество Мандельброта
Мы уже убедились в том, что множества Жюлиа функции f(z)=z2+c обладают
Множество Мандельброта
Мы уже убедились в том, что множества Жюлиа функции f(z)=z2+c обладают

f(z)=z2-1.2i
f(z)=z2+0.5
f(z)=z2+0.31+0.04i
Слайд 57Множество Мандельброта (см. рисунок) M для полинома fс(z)=z2+c определяется как множество всех
Множество Мандельброта (см. рисунок) M для полинома fс(z)=z2+c определяется как множество всех
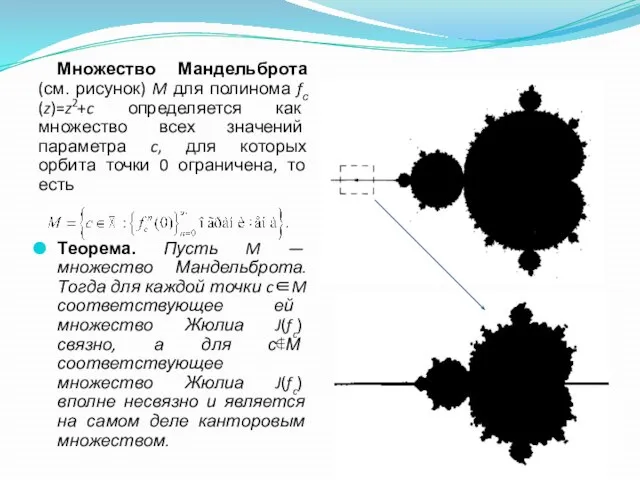
Теорема. Пусть M — множество Мандельброта. Тогда для каждой точки c∈M соответствующее ей множество Жюлиа J(fc) связно, а для с∉М соответствующее множество Жюлиа J(fc) вполне несвязно и является на самом деле канторовым множеством.
Слайд 58Упражнения 7
Покажите, что множество Мандельброта симметрично относительно вещественной оси. Для этого покажите,
Упражнения 7
Покажите, что множество Мандельброта симметрично относительно вещественной оси. Для этого покажите,

топологически сопряжены. Затем исследуйте орбиты точки 0 при этих двух отображениях.
Используя программу, постройте изображения множеств Жюлиа и Мандельброта для функций f(z)=zn+c при различных n. Проверьте выполнение условий предыдущей теоремы при n≠2.
Слайд 59Проблема Кэли
В 1879 году сэр Артур Кэли поставил задачу итерирования комплексных
Проблема Кэли
В 1879 году сэр Артур Кэли поставил задачу итерирования комплексных

Метод Ньютона для нахождения вещественного корня f(x) заключается в следующем. Выберем начальное приближение x0, вычислим точки
и найдем предел limn→∞ xn. Предполагается, что f, f’, и f’’ существуют и непрерывны в окрестности нуля функции, скажем, при x=c, то есть f(c)=0, причем f’(c)≠0. Заметим, что точка c является сверхпритягивающей неподвижной точкой для функции
то есть g(c)=c и g’(c)=0. Таким образом, если x0 находится достаточно близко к c, то limn→∞xn=c.
Слайд 60Для f(x)=х3-1 единственный вещественный ноль функции равен 1, и итерации Ньютона принимают
Для f(x)=х3-1 единственный вещественный ноль функции равен 1, и итерации Ньютона принимают

Кэли предложил исследовать поведение этих итераций для комплексных zn:
Имеются три кубических корня из 1:
Областью притяжения для корня wk назовем множество
Кэли поставил задачу описания областей A(w1), A(w2) и A(w3).
Слайд 61Как и в случае вещественных итераций, если начальная точка z0 находится достаточно
Как и в случае вещественных итераций, если начальная точка z0 находится достаточно

Перед исследованием проблемы Кэли для кубических корней рассмотрим соответствующую задачу для квадратных корней. В этом случае f(z)=z2-1 и ньютоновские итерации имеют вид:
Если z0 лежит в правой полуплоскости, то zn→1 при n→∞, а если z0 лежит в левой полуплоскости, то zn→-1 при n→∞ (см. упр. 8). Таким образом, за исключением начальных точек z0, которые равноудалены от двух корней, zn сходится к корню, ближайшему к zn . Если z0 лежит на мнимой оси, то в этом случае итерации не сходятся (см. упр. 8).
По аналогии со случаем z2-1 можно предположить, что в случае z3-1 итерированные значения zn сходятся к кубическому корню, ближайшему к z0, если такой ближайший корень существует. Таким образом, ответ на вопрос Кэли предположительно выглядит так, как показано на рисунке. Как ни странно, это предположение оказывается неверным в силу следующей теоремы.
A(w2)
A(w3)
A(w1)
Слайд 62Теорема. Границы всех областей притяжения A(wk) совпадают.
Теорема говорит нам о том,
Теорема. Границы всех областей притяжения A(wk) совпадают.
Теорема говорит нам о том,

Иными словами, мы получили ответ на следующий вопрос: как закрасить плоскость тремя красками, чтобы на границе каждой цветной области существовали точки двух других цветов, которые были бы расположены произвольно близко?
 Материалы для автоворонки
Материалы для автоворонки Презентация на тему Плоские черви
Презентация на тему Плоские черви  Фотоискусство
Фотоискусство lektsia_6
lektsia_6 Методы развития внимания у детей дошкольного возраста
Методы развития внимания у детей дошкольного возраста  Буддизм
Буддизм Аэрозоль
Аэрозоль Энергосбережение при грануляции металлургического шлака
Энергосбережение при грануляции металлургического шлака История династии Романовых
История династии Романовых Аксиологические основы профессиональной подготовки студентов международного профиля
Аксиологические основы профессиональной подготовки студентов международного профиля Подарок юной рукодельнице
Подарок юной рукодельнице Белорусский костюм (1)
Белорусский костюм (1) Врачебный диагноз
Врачебный диагноз Wide Range of UPVC Windows & Doors
Wide Range of UPVC Windows & Doors Агляд-конкурс мастацкай самадзейнай творчасці сярод груп першага курса Я - беларус. Я - зерне, код народа
Агляд-конкурс мастацкай самадзейнай творчасці сярод груп першага курса Я - беларус. Я - зерне, код народа Информационное сообщениеВ.Н. Федулин
Информационное сообщениеВ.Н. Федулин Front Page
Front Page МАДОУ детский сад «Надежда» г.Кирово-Чепецк Кировская область Коррекционно-педагогическая работа с использованием ло
МАДОУ детский сад «Надежда» г.Кирово-Чепецк Кировская область Коррекционно-педагогическая работа с использованием ло «5 факторов эффективного поискового продвижения
«5 факторов эффективного поискового продвижения маркетинговые коммуникации
маркетинговые коммуникации  Олимпиады школьников по направлению «Информационная безопасность»
Олимпиады школьников по направлению «Информационная безопасность» От Сиднея вдоль Большого Водораздельного хребта
От Сиднея вдоль Большого Водораздельного хребта Презентация на тему Водоросли
Презентация на тему Водоросли  7 февраля 2006 г. Пресс-конференция «Вырваться из Сумрака!»
7 февраля 2006 г. Пресс-конференция «Вырваться из Сумрака!» Кластерный анализ. Метод к – средних
Кластерный анализ. Метод к – средних СЕМЕЙНЫЙ КЛУБ «МАМИНЫ ГЛАЗА»
СЕМЕЙНЫЙ КЛУБ «МАМИНЫ ГЛАЗА» Обзор зарплат по должностям дилерских авто центров
Обзор зарплат по должностям дилерских авто центров Преступление. Разновидности преступлений
Преступление. Разновидности преступлений