Содержание
- 2. Линейная функция Обратная пропорциональность Задачи ГИА Квадратичная функция Свойства функций Построение графика кусочной функции и её
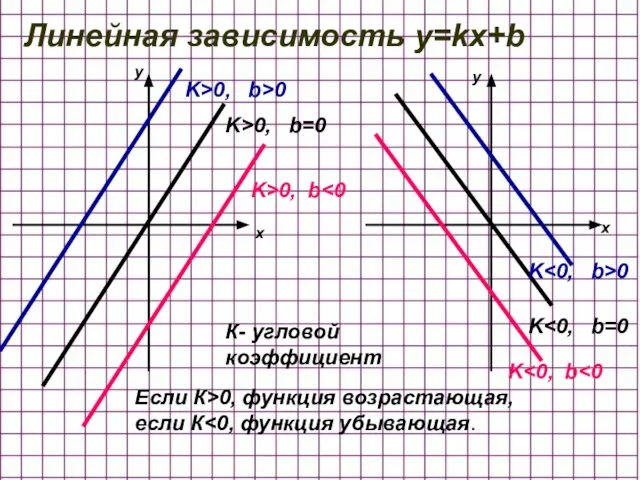
- 3. Линейная зависимость y=kx+b K>0, b>0 K>0, b=0 K>0, b K K K 0 x x К-
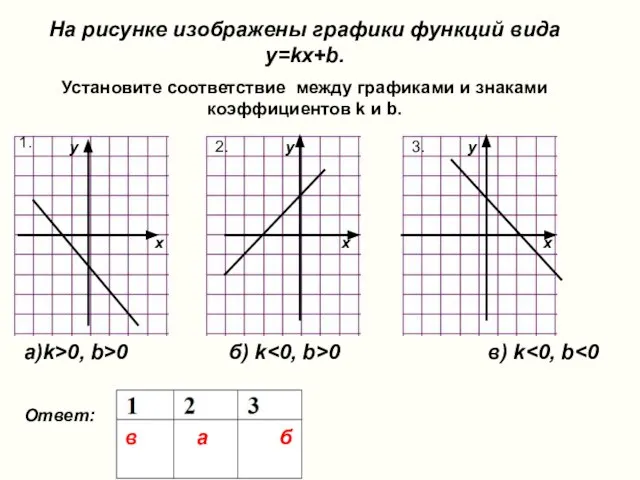
- 4. На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками и знаками коэффициентов k и
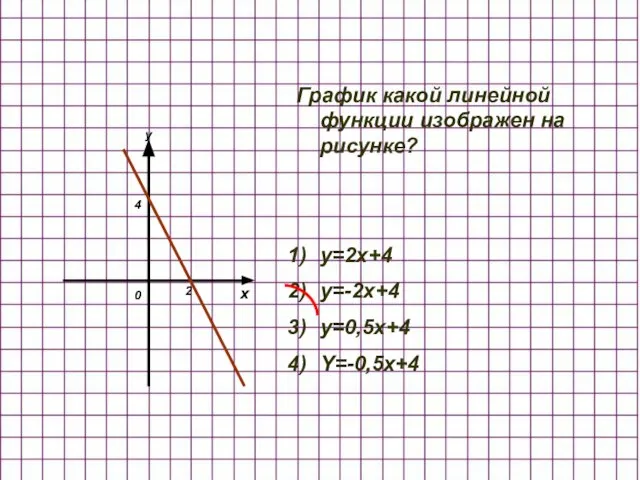
- 5. x y 2 4 График какой линейной функции изображен на рисунке? y=2x+4 y=-2x+4 y=0,5x+4 Y=-0,5x+4 0
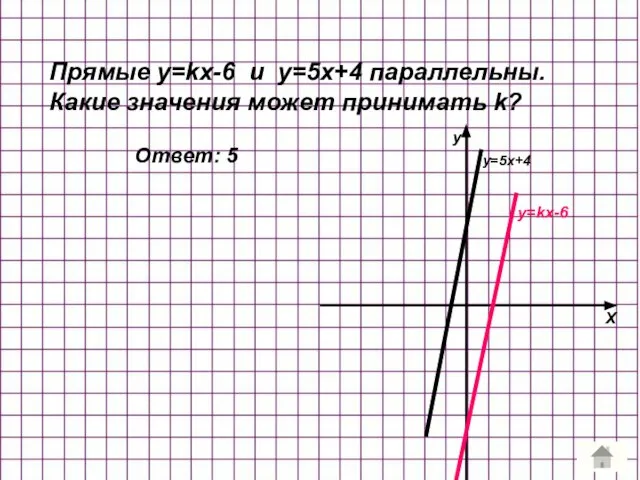
- 6. Прямые y=kx-6 и у=5x+4 параллельны. Какие значения может принимать k? Ответ: 5 X y y=kx-6 у=5x+4
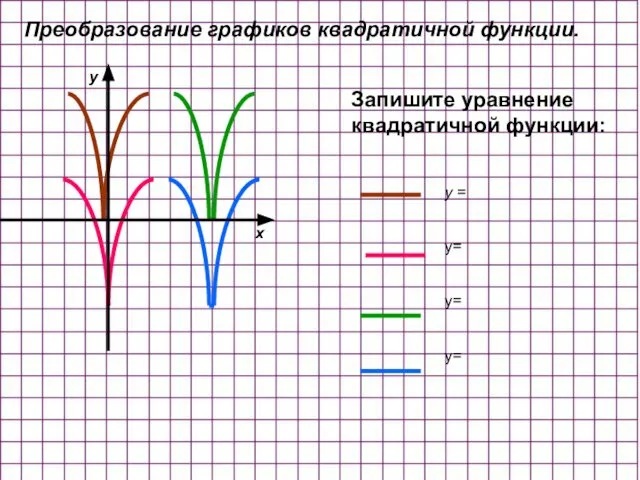
- 7. Запишите уравнение квадратичной функции: y = y= y= y= Преобразование графиков квадратичной функции. x y
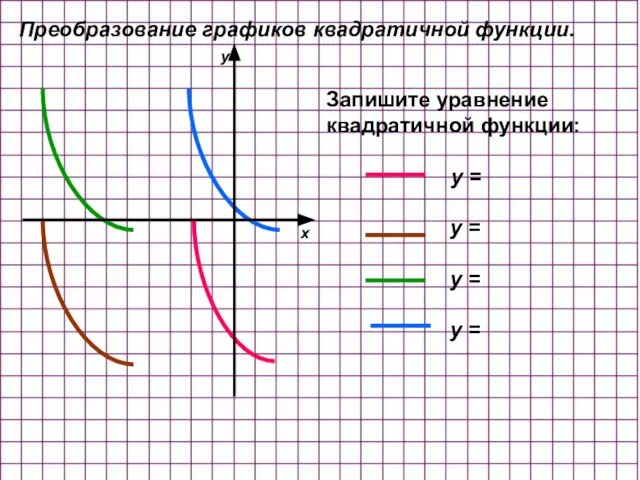
- 8. Запишите уравнение квадратичной функции: y = y = y = y = Преобразование графиков квадратичной функции.
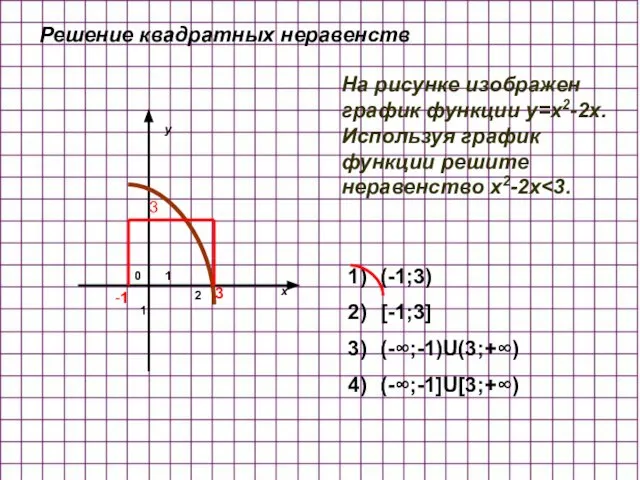
- 9. 0 1 1 2 х y На рисунке изображен график функции y=x2-2x. Используя график функции решите
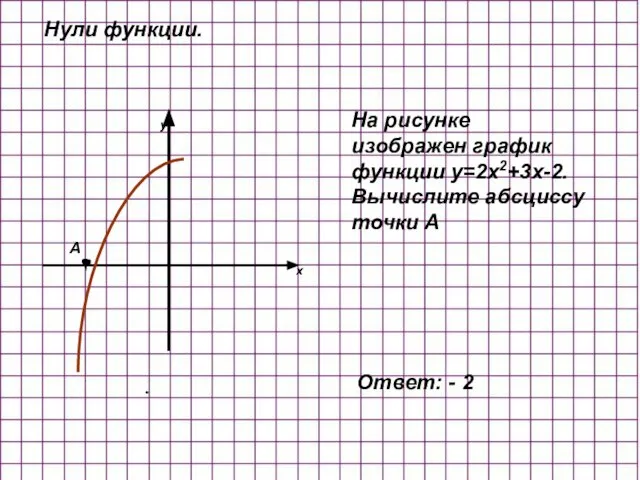
- 10. Нули функции. x y A На рисунке изображен график функции y=2x2+3x-2. Вычислите абсциссу точки А Ответ:
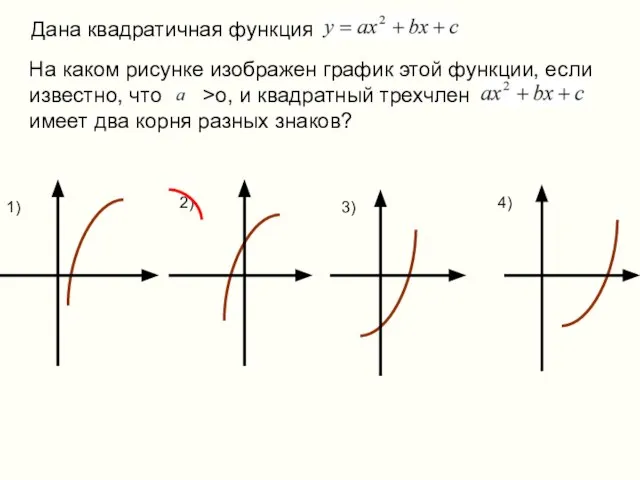
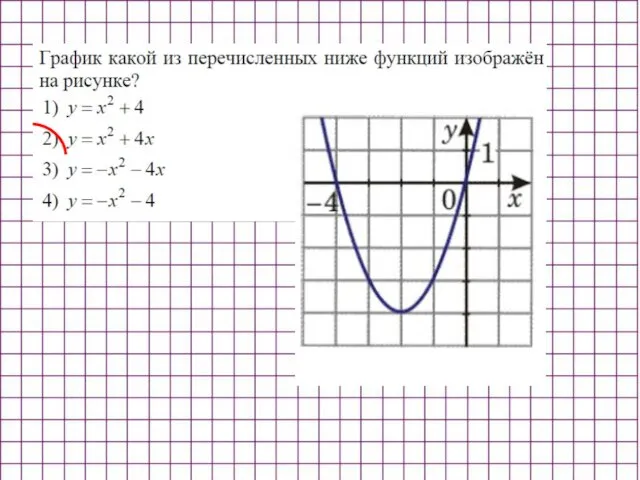
- 11. На каком рисунке изображен график этой функции, если известно, что >o, и квадратный трехчлен имеет два
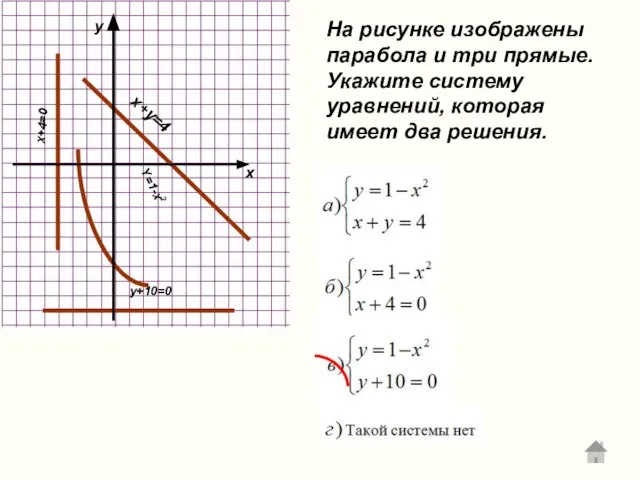
- 13. Y=1-x2 x+4=0 x+y=4 y+10=0 На рисунке изображены парабола и три прямые. Укажите систему уравнений, которая имеет
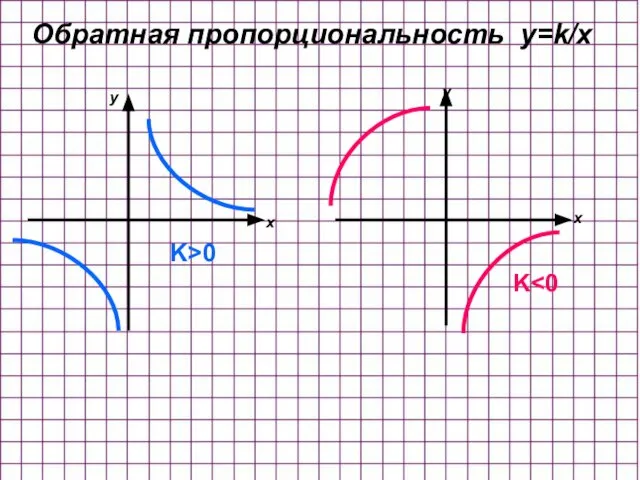
- 14. Обратная пропорциональность y=k/x K>0 K x x y y
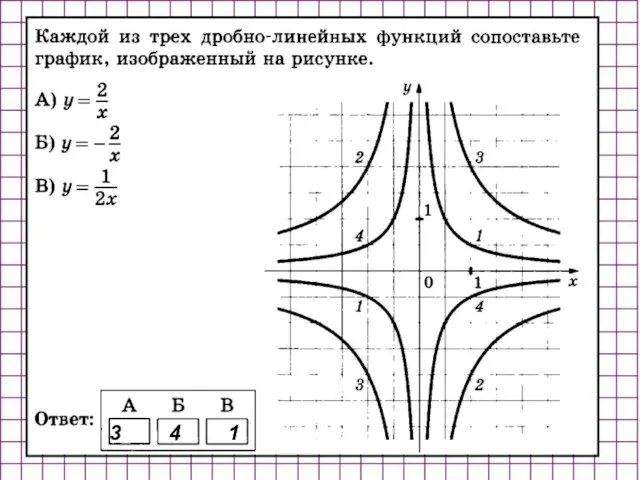
- 15. 3 4 1
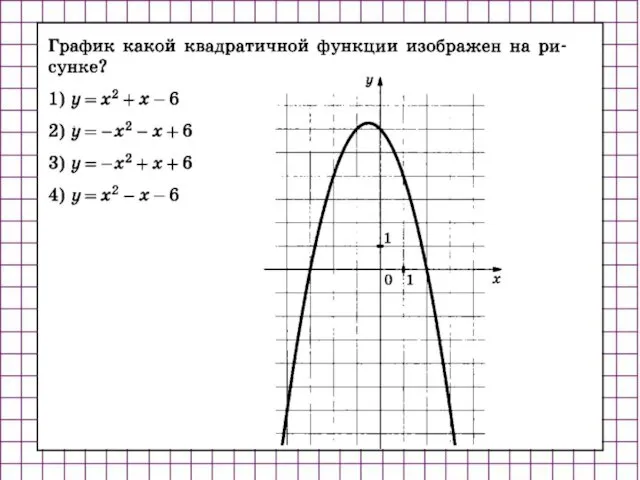
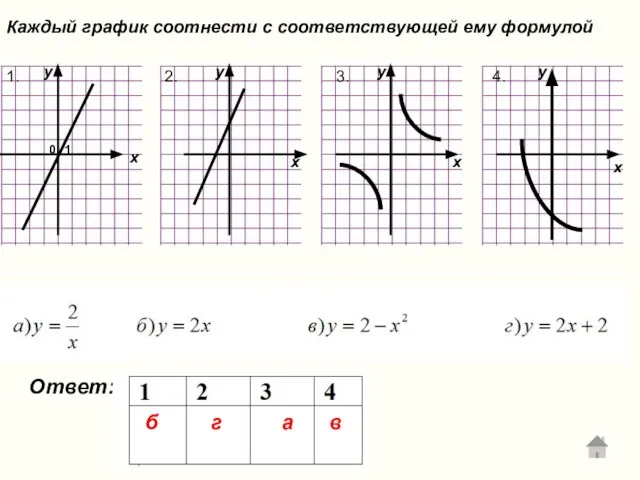
- 16. Каждый график соотнести с соответствующей ему формулой Ответ: 1. 2. 3. 4. б г а в
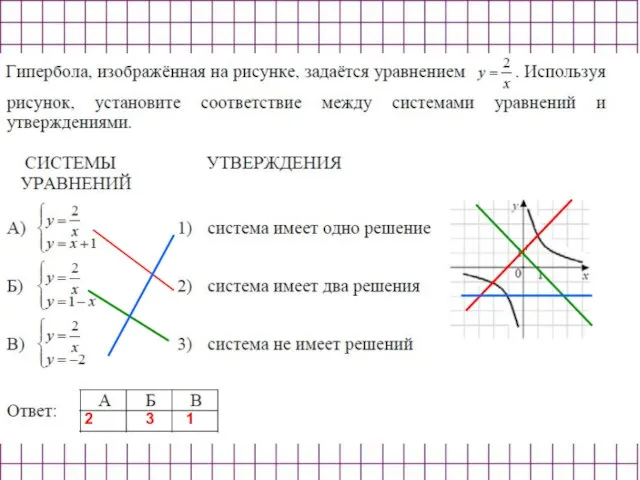
- 18. 2 3 1
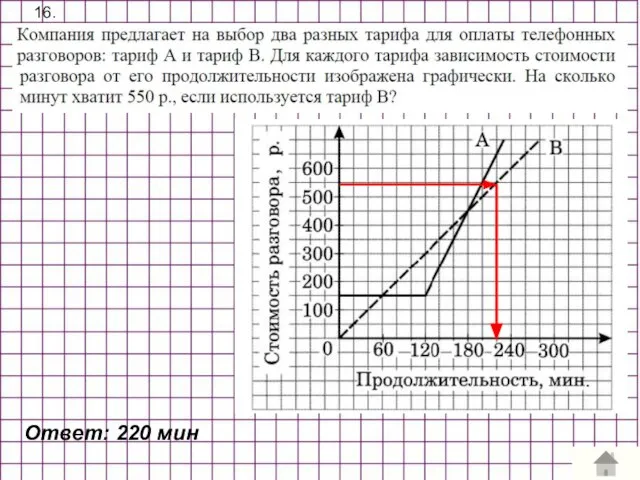
- 19. 16. Ответ: 220 мин
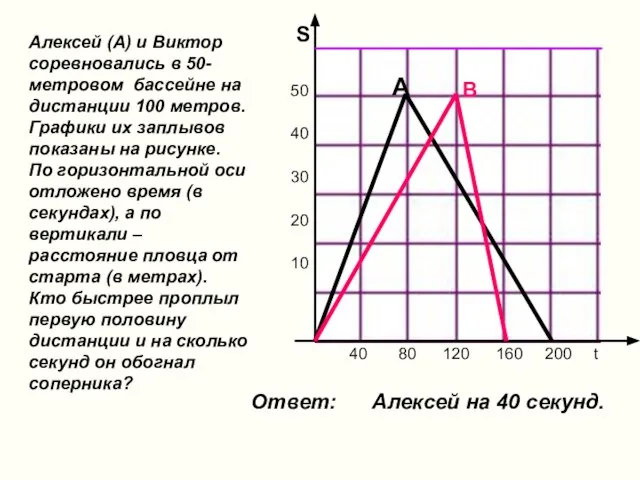
- 20. Алексей (А) и Виктор соревновались в 50-метровом бассейне на дистанции 100 метров. Графики их заплывов показаны
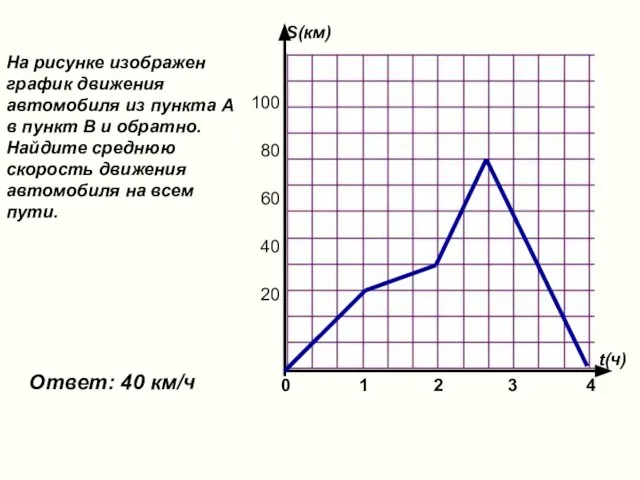
- 21. 0 1 2 3 4 t(ч) S(км) 100 80 60 40 20 На рисунке изображен график
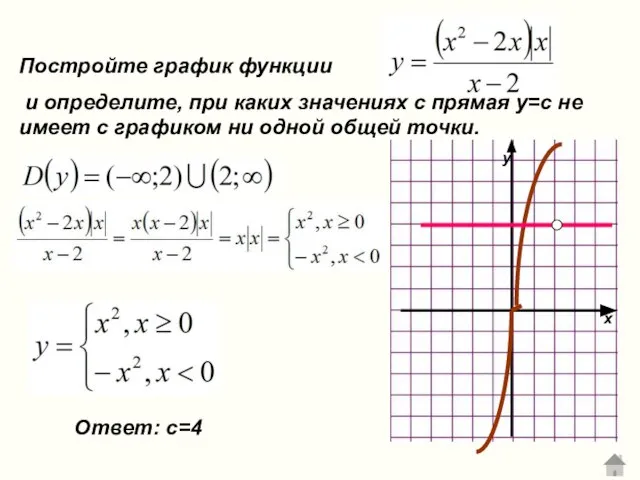
- 22. Постройте график функции и определите, при каких значениях с прямая у=с не имеет с графиком ни
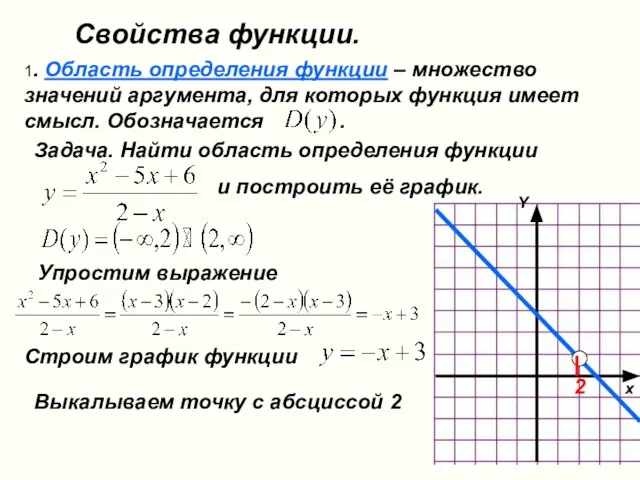
- 23. Свойства функции. 1. Область определения функции – множество значений аргумента, для которых функция имеет смысл. Обозначается
- 24. 2. Область значений, ограниченность. Область значений – множество значений функции, обозначается Функция ограничена снизу, если для
- 25. Функция задана графиком, на области определения [-3;7], найдите её наименьшее и наибольшее значения, укажите x y
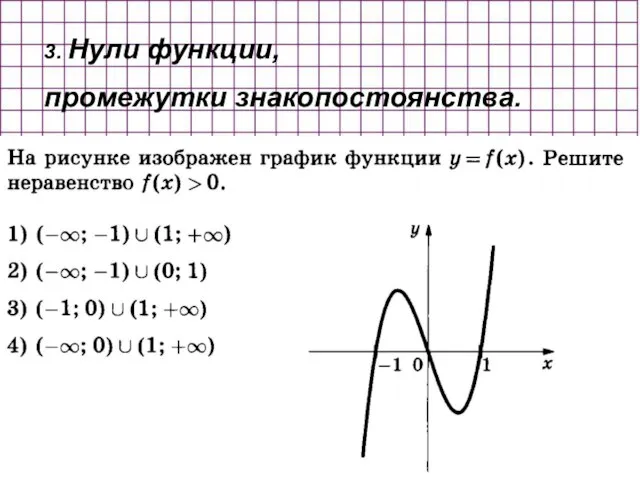
- 26. 3. Нули функции, промежутки знакопостоянства.
- 27. 4. Монотонность функции. Функция называется возрастающей на множестве Х, если большему значению аргумента соответствует большее значение
- 28. Задача. По графику функции, область определения которой [-6,7], укажите промежутки монотонности функции. Х -3 1 3
- 29. 5. Четность и нечетность функций. Функция называется четной, если для любого верно равенство Функция называется нечетной,
- 30. Задача. Дан фрагмент графика нечетной функции которая определена на [-7;7] достройте график и заполните пропуски. x
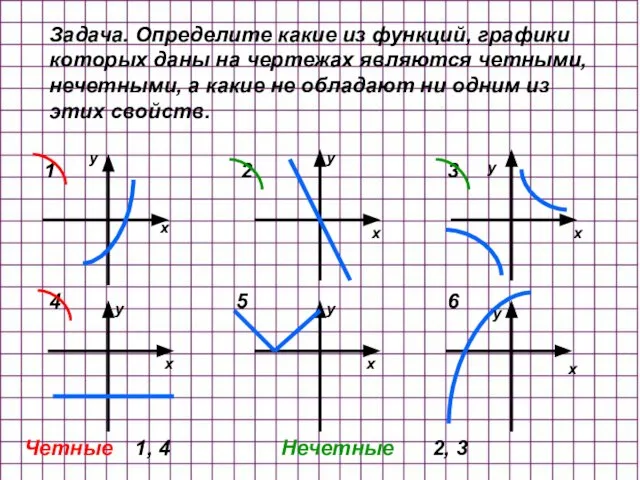
- 31. Задача. Определите какие из функций, графики которых даны на чертежах являются четными, нечетными, а какие не
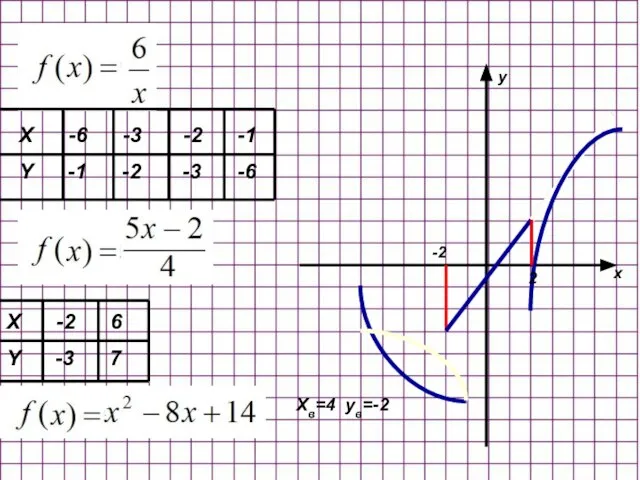
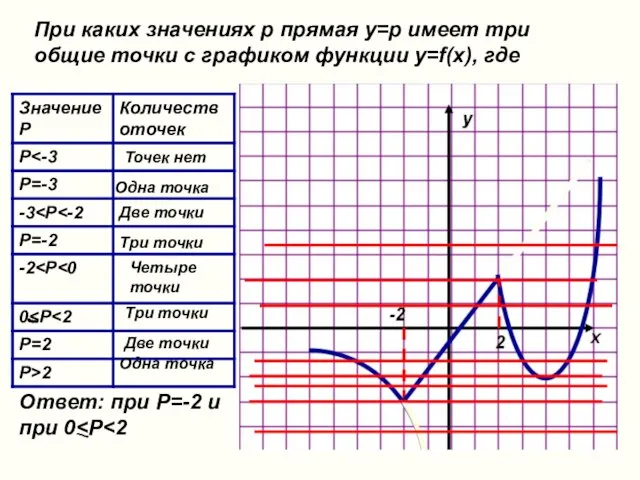
- 32. При каких значениях p прямая y=p имеет три общие точки с графиком функции y=f(x), где Построение
- 33. X -6 -3 -2 -1 Y -1 -2 -3 -6 -2 X -2 6 Y -3
- 34. При каких значениях p прямая y=p имеет три общие точки с графиком функции y=f(x), где Точек
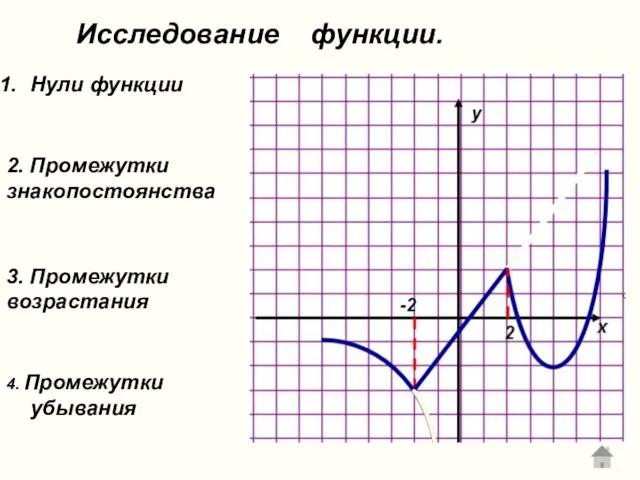
- 35. Исследование функции. Нули функции 3. Промежутки возрастания 4. Промежутки убывания 2. Промежутки знакопостоянства
- 36. Тест по теме функции и графики №1
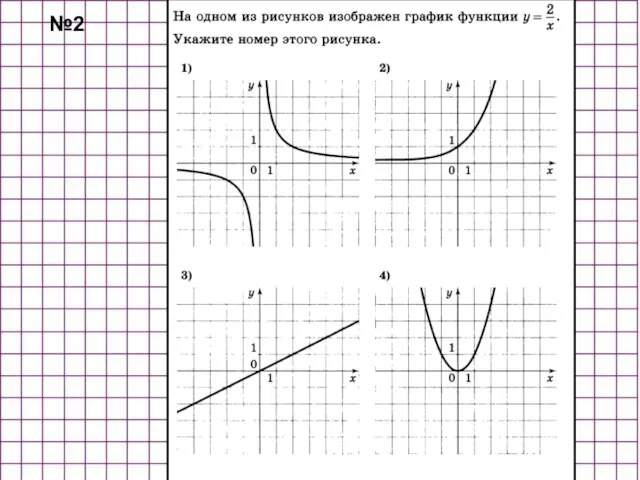
- 37. №2
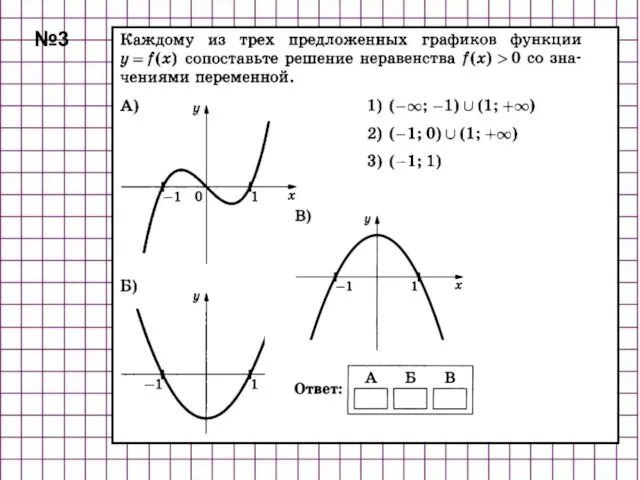
- 38. №3
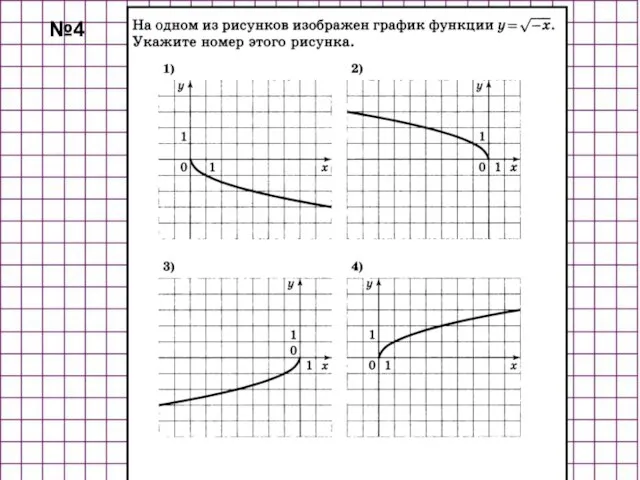
- 39. №4
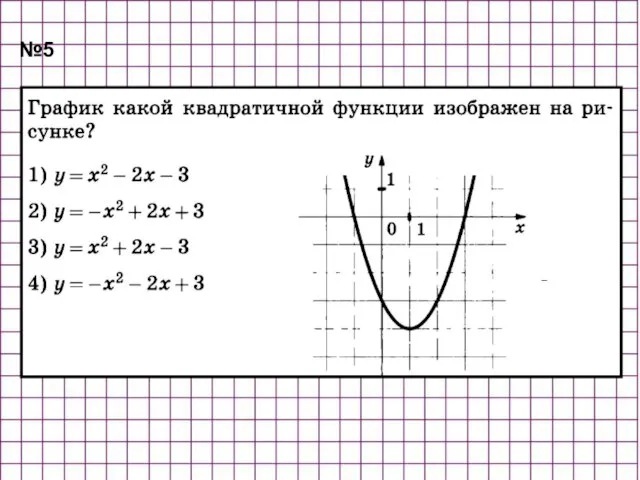
- 40. №5
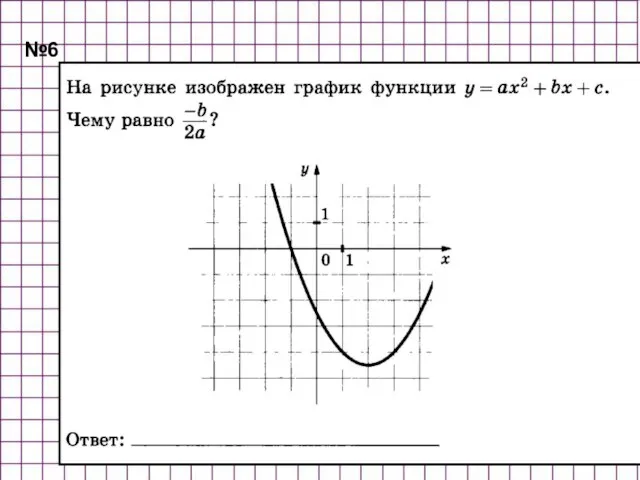
- 41. №6
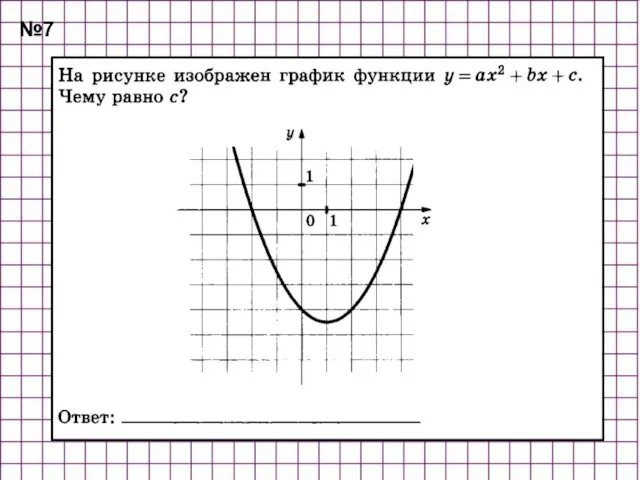
- 42. №7
- 44. Скачать презентацию


![Функция задана графиком, на области определения [-3;7], найдите её наименьшее и наибольшее](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/397907/slide-24.jpg)

![Задача. По графику функции, область определения которой [-6,7], укажите промежутки монотонности функции.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/397907/slide-27.jpg)

![Задача. Дан фрагмент графика нечетной функции которая определена на [-7;7] достройте график](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/397907/slide-29.jpg)


 Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной
Висит за окошком Кулёк ледяной, Он полон капели И пахнет весной Средства регулирования движением поездов
Средства регулирования движением поездов Афины при Перикле
Афины при Перикле Электронная таблица EXCEL
Электронная таблица EXCEL Архетипы
Архетипы УНИДРУА: международный институт по унификации частного права
УНИДРУА: международный институт по унификации частного права Органы чувств
Органы чувств  «Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения»
«Этимологический анализ прозвищ жителей деревень Завражье, Мешково и поселка Судоверфь Судоверфского сельского поселения» Новогодние открытки
Новогодние открытки Робототехника. Проект
Робототехника. Проект Балансирующий рынок
Балансирующий рынок Теорема Пифагора
Теорема Пифагора Культура XX века
Культура XX века Деревня Юрьевец
Деревня Юрьевец Wine. The benefits of wine with moderate consumption
Wine. The benefits of wine with moderate consumption Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов
Биопсихосоциодуховный подход к профилактике профессионального выгорания психологов Воздействие высокоскоростных магистралей на окружающую среду
Воздействие высокоскоростных магистралей на окружающую среду Презентация экскурсии в животноводческий комплекс «ИП Каюмов»
Презентация экскурсии в животноводческий комплекс «ИП Каюмов» 07_0___163
07_0___163 каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в
каждую неделю около 600 000 слушателей включаются на частоту 100,5 FM каждый день Радио BEST FM слушают около 300 000 человек каждые 15 минут на в «Белые» в Гражданской войне
«Белые» в Гражданской войне Внедрение здоровьесберегающих технологий
Внедрение здоровьесберегающих технологий Русское искусство 2 пол.19 века
Русское искусство 2 пол.19 века Всегда ли правы мы- родители?
Всегда ли правы мы- родители? Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова
Итоги работы отрасли в 2010 году и задачи на 2011 год Глава департамента Елена Борисовна Чеснокова Семейные традиции семьи Митрофановых
Семейные традиции семьи Митрофановых HADI – это экспериментальный научный метод исследования, переложенный на бизнес
HADI – это экспериментальный научный метод исследования, переложенный на бизнес ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс
ПРОЕКТ КНИЖКА-САМОДЕЛКА «Волшебница Зима» 4 класс