Функции нескольких переменных

Литература
Основная литература:
Л. Д. Кудрявцев. Курс математического анализа, т. 1, 2 Г. Н. Берман. Сборник задач по курсу математического анализа.
Н. С. Пискунов. Дифференциальное и интегральное исчисления, т. 1, 2.

Дополнительная литература:
Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах, ч. 1, 2.

Учебно-методические разработки:
Л. Я. Дубинина, Л. С. Никулина, И. В. Пивоварова. Курс лекций по высшей математике, ч. 1, 2.-Владивосток, изд. ВГУЭиС, 2001.
Сборник задач по высшей математике. Сост. И. В. Пивоварова, Л. Я. Дубинина, Л. С. Никулина. -Владивосток, изд. ВГУЭиС, 2002.

Содержание
Функции нескольких переменных
Дифференциальные уравнения 1-го, 2-го и более высокого порядков
Кратные интегралы
Числовые ряды
Степенные ряды
Ряды Фурье

Функции нескольких переменных
Лекция 1

Определение функции двух переменных
Определение. Если каждой паре (x,y) значений двух независимых друг от друга переменных величин x и y из некоторого множества D соответствует единственное значение величины z, а каждому z соответствует хотя бы одна пара (x,y), то мы говорим, что z есть функция двух независимых переменных x и y, определенная в D.

Обозначения
При этом пишут:
Если паре соответствует число , то пишут
Или называется частным значением функции при

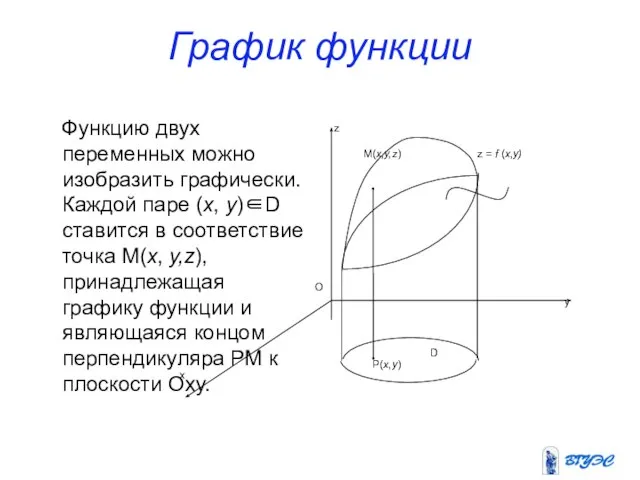
График функции 2-х переменных
Геометрическое место точек, координаты которых удовлетворяют уравнению z= =f(x,y), называется графиком функции двух переменных.

График функции
Функцию двух переменных можно изобразить графически. Каждой паре (x, y)∈D ставится в соответствие точка M(x, y,z), принадлежащая графику функции и являющаяся концом перпендикуляра PM к плоскости Oxy.

Предел функции 2-х переменных
Окрестностью радиуса R точки
называется совокупность всех точек, лежащих внутри круга радиуса R с центром в точке , кроме самой точки.

Предел функции 2-х переменных
Таким образом, окрестностью точки является множество точек,
УДОВЛЕТВОРЯЮЩИХ НЕРАВЕНСТВУ
.
о
х
у

Определение предела функции 2-х переменных
Число А называется пределом функции z=f(x,y) при , если для любого числа найдется такое число R>0, что для всех точек М(х,у), лежащих в окрестности радиуса R точки , выполняется условие
При этом пишут: или

Непрерывность
Функция z=f(x,y) называется непрерывной в точке , если выполнены условия:
1)функция определена в точке ,
2)если существует ,
3)если

Непрерывность
Другое определение: Функция z=f(x,y)
называется непрерывной в точке , если в этой точке бесконечно малому приращению аргументов соответствует бесконечно малое приращение функции, т. е.
где .

Внутренние и граничные точки
Линию, ограничивающую некоторую область D в плоскости Oxy, мы будем называть границей этой области.
Точки области, не лежащие на границе области, мы будем называть внутренними точками области, если они принадлежат области вместе со своей окрестностью.
Теорема. Если функция f (x, y)
μ .

Открытая и замкнутая области
Область, состоящую из одних внутренних точек, мы будем называть открытой или незамкнутой.
Если же к области относятся еще и точки границы, то область называют замкнутой.

Ограниченная область
Область называют ограниченной, если существует такое постоянное C>0, что расстояние любой точки M области от начала координат O меньше C, т.е. .

Наибольшее и наименьшее значения функции
Теорема Вейерштрасса. Непрерывная функция в замкнутой ограниченной области D достигает по крайней мере один раз наибольшего значения M и наименьшего значения m.

Частные приращения функции 2-х переменных
Разность = f (x+Δx, y) – f (x, y) называется частным приращением функции f (x, y) по переменной x.
Разность = f (x, y+Δy) – f (x, y) называется частным приращением функции f (x, y) по переменной y.

Частные производные
Определение. Если существует
= ,
то он называется частной производной (первого порядка) функции z = f (x, y) по переменной x и обозначается

Продолжение
Аналогично определяется частная производная по переменной y:
=
Эту производную обозначают

Производные высших порядков
Частной производной n-го порядка функции нескольких переменных называется частная производная первого порядка от частной производной (n-1)-го порядка той же функции. Например, для функции 2-х переменных имеем: