Функция

Определение функции.
Функция –
одно из важнейших
математических понятий
Функцией называют такую зависимость переменной у от переменной х,
при которой
каждому значению переменной х соответствует единственное значение переменной у

Функция
у
Переменную
x
называют
независимой переменной ,
или
аргументом
Переменную
у
называют
зависимой переменной
Говорят также, что
переменная у
является функцией от переменной х

D(y) и E(y) функции
Все значения
независимой переменной
х
образуют
область
определения функции – D(y)
Все значения ,
которые принимает
зависимая переменная
у
образуют
область значений
функции – E(y)

Найти D(y) и E(y) функции:
y = 3x-5
y = -2x/3
y = 3/2x
y = √1-2x
y = 11sin x
y = lg (4x-1)
x Є R
x Є R
y Є R
y Є R
x Є (-∞;0)U(0; ∞)
x Є (-∞;0,5]
x Є R
x Є (0,25; ∞)
y Є [0; ∞)
y Є [-11; 11]
y Є R
уЄ (-∞;0)U(0; ∞)

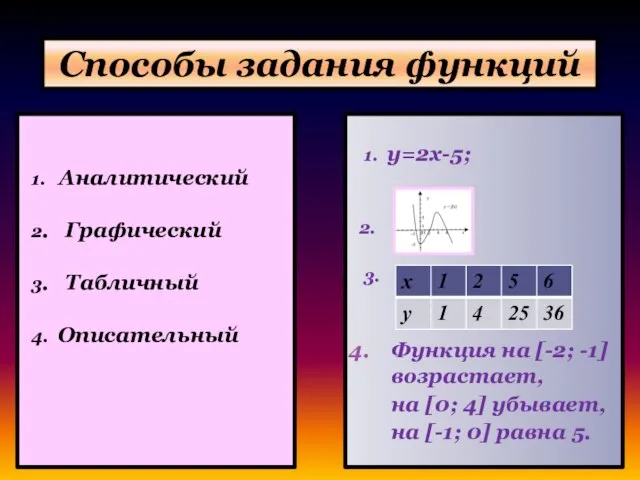
Способы задания функций
1. Аналитический
2. Графический
3. Табличный
4. Описательный
1. y=2x-5;
2.
3.
Функция на [-2; -1] возрастает,
на [0; 4] убывает,
на [-1; 0] равна 5.

График функции
Графиком функции
называют множество всех точек координатной плоскости,
абсциссы которых равны значениям аргумента,
а ординаты- соответствующим значениям функции.

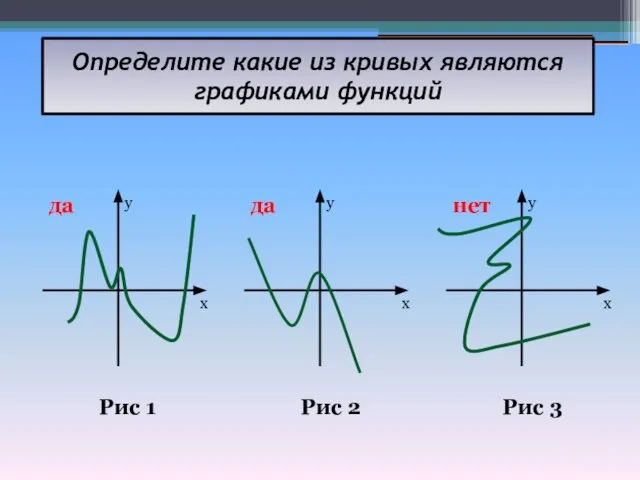
Определите какие из кривых являются графиками функций
Рис 1
Рис 2
Рис 3
y
x
y
x
y
x
да
да
нет

Свойства функций
1. Чётность:
Свойство графика
Функция называется чётной если:
D(y) симметрична относительно 0,
для любого х из D(y) выполняется условие f(x)= f(-x)
График чётной функции
симметричен относительно
оси ординат.

Свойства функций
Нечётность
Свойство графика
Функция называется
нечётной если
D(y) симметрична относительно 0,
для любого х из D(y) выполняется условие
f(-x)= -f(x)
График нечётной функции
симметричен относительно начала координат.

Свойства функций
Монотонность
Свойство графика
Функция возрастает
[или убывает] на промежутке I, если для любого х Є I выполняется условие :
при х1>х2 f(х1)>f(х2)
[при х1>х2 f(х1)

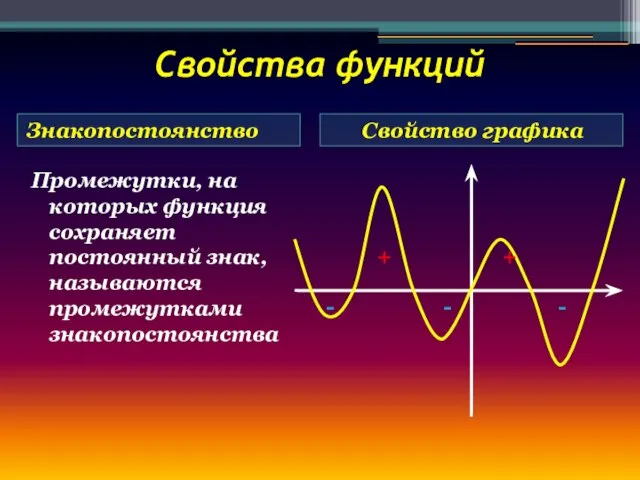
Свойства функций
Знакопостоянство
Свойство графика
Промежутки, на которых функция сохраняет постоянный знак, называются промежутками знакопостоянства
+ +
-
-
-

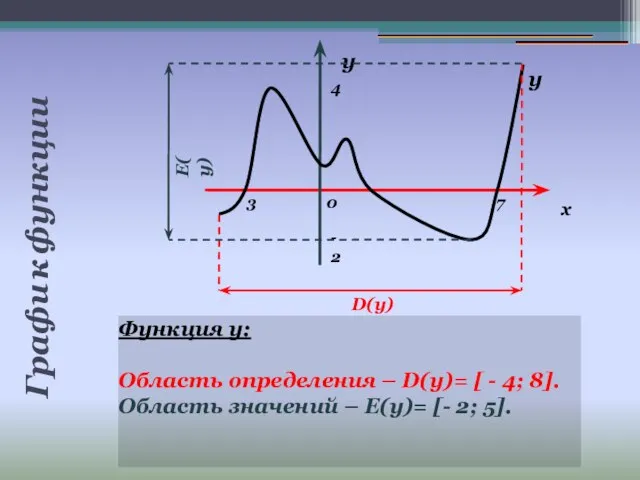
Графи к функции
Функция у:
Область определения – D(y)= [ - 4; 8].
Область значений – E(y)= [- 2; 5].
х
у
-2
4
0
3
7
y
D(y)
E(y)

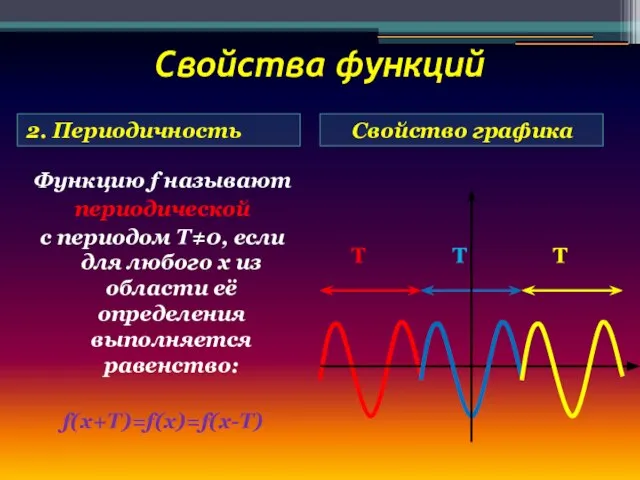
Свойства функций
2. Периодичность
Свойство графика
Функцию f называют
периодической
с периодом Т≠0, если для любого х из области её определения выполняется равенство:
f(x+T)=f(x)=f(x-T)
Т
Т
Т

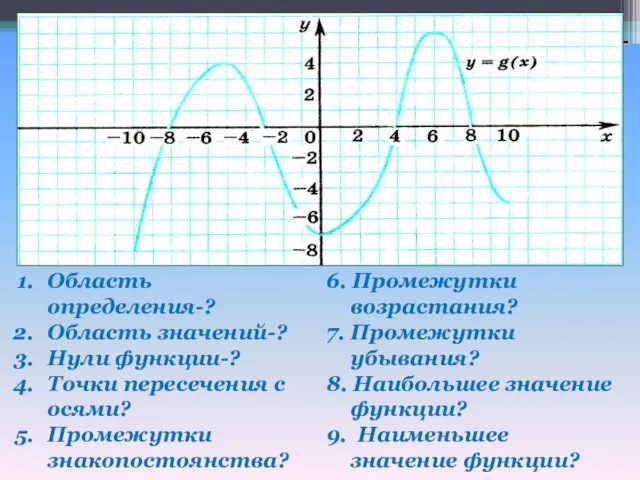
Область определения-?
Область значений-?
Нули функции-?
Точки пересечения с осями?
Промежутки знакопостоянства?
6. Промежутки возрастания?
7. Промежутки убывания?
8. Наибольшее значение функции?
9. Наименьшее значение функции?