Функция у=кх2, ее свойства и график

Математику уже затем учить надо, что она ум в порядок приводит.
М.В.Ломоносов

Девиз урока:
«Дорогу осилит идущий, а математику- мыслящий»

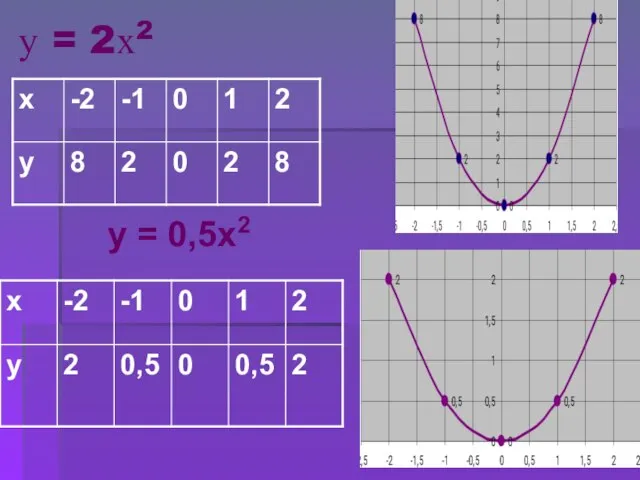
у = 2х2
у = 0,5х2

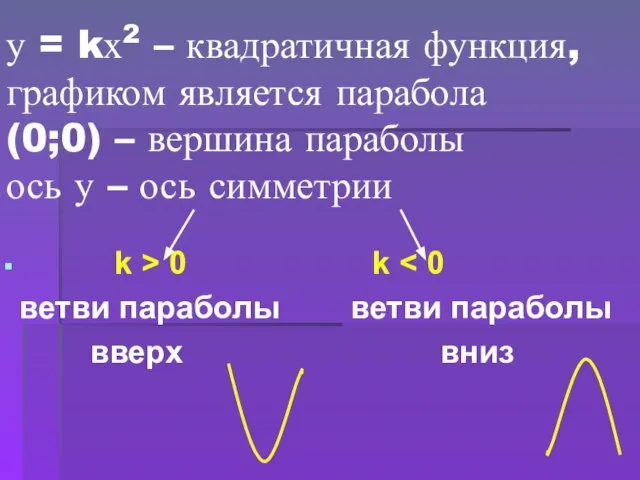
у = kх2 – квадратичная функция, графиком является парабола
(0;0) – вершина параболы
ось у – ось симметрии
k > 0 k < 0
ветви параболы ветви параболы
вверх вниз

График функции у = -f(x) симметричен графику функции у = f(x) относительно оси абсцисс.

Свойства функции у=кх2
при к > 0

1.D(f) = (-∞;+∞)
2. у = 0 при х = 0
у > 0 при х є (-∞; 0) U (0;+∞), 3.непрерывна
4.унаим = 0, унаиб = не сущ.
5. убывает при х є (-∞;0],
возрастает при хє [0; +∞)
6.ограничена снизу,
не ограничена сверху
7.Е(f) = [0; +∞)
8.выпукла вниз.

Свойства функции у = kх2
при k < 0
1. D(f) = (-∞; +∞)
2. у = 0 при х = 0 , У < 0 при х є (-∞; 0) U (0; +∞),
3. Непрерывна
4. Унаим = не сущ., унаиб = 0 (при х=0)
5. возрастает при х є (-∞; 0],
убывает при х є [0; +∞)
6.Ограничена сверху, не ограничена снизу
7. Е(f) = (-∞; 0]
8. выпукла вверх.

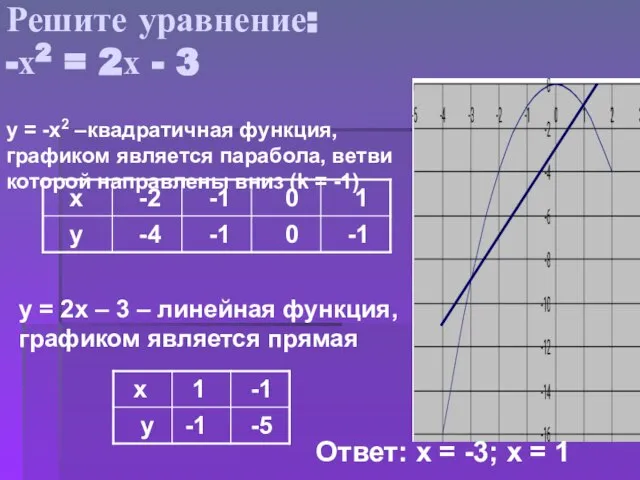
Решите уравнение:
-х2 = 2х - 3
у = -х2 –квадратичная функция, графиком является парабола, ветви которой направлены вниз (k = -1)
у = 2х – 3 – линейная функция, графиком является прямая
Ответ: х = -3; х = 1

Вариант 1.
При каком значении аргумента х значение функции у= 0,5х2 равно 2 ?
1)-1 и 1 2) 2 3) -2 и 2
4) -0,5 и 0,5
Графику функции у = -50 х2 принадлежит точка с координатами
1)(-4;-800) 2) (-4; 800) 3) (-4; 200) 4) (-4; -200)
Прямая у =5х-1 пересекает параболу у =2х2
1)в одной точке 2) в двух точках
3)в трех точках 4) не пересекает

Вариант -2.
1. При каком значении аргумента х значение функции у= - 0,25 х2 равно -4 ?
1)-1 и 1 2) 4 3) - 0,25 и 0,25 4) -4 и 4
2. Графику функции у =80 х2 принадлежит точка с координатами
1)(-5;-200) 2) (-5; 2000) 3) (-5; -2000) 4) (-5; -200)
Прямая у =2х+7 пересекает параболу у =3х2
1)в одной точке 2) в двух точках
3)в трех точках 4) не пересекает

Ответы
В-1 3,1,4
В -2 4,2,2

Спасибо за урок

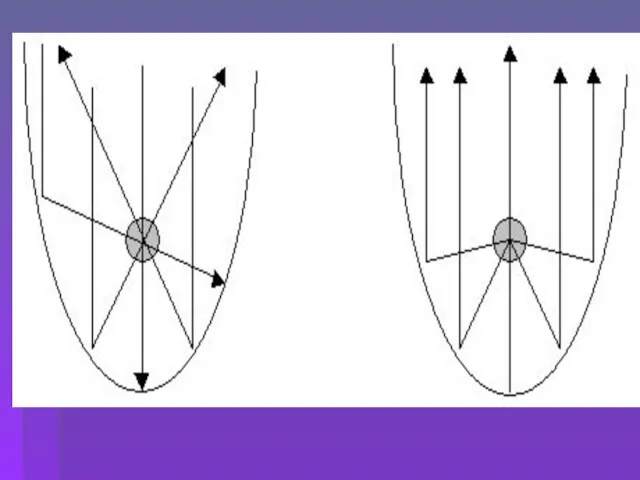
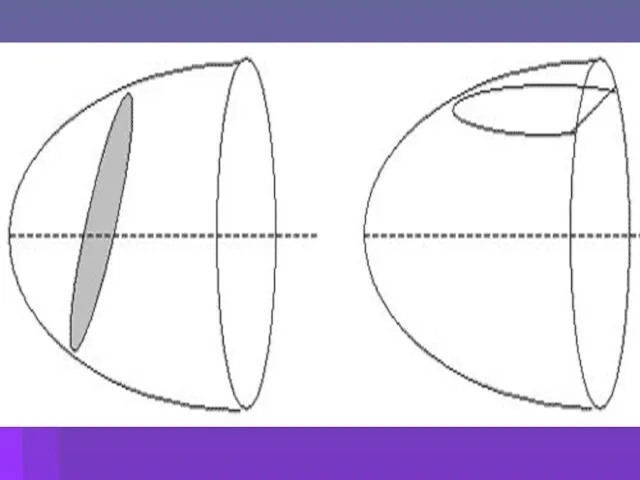
О замечательных
свойствах параболы

Применение параболы в природе