Функции издержек

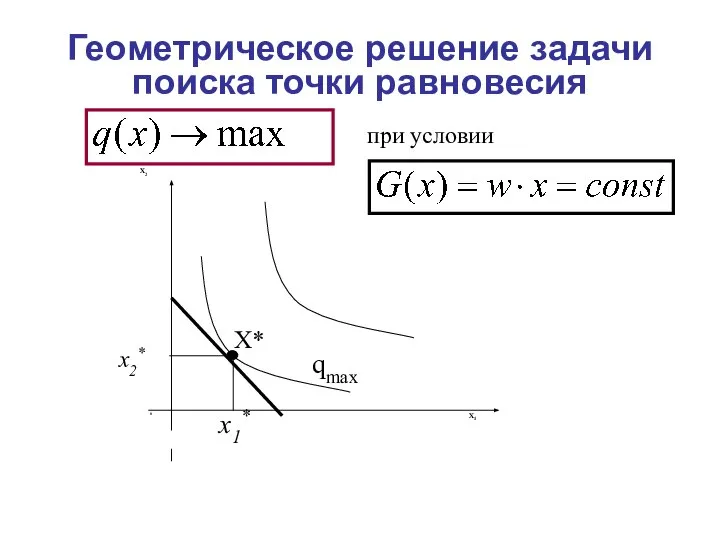
Точка равновесия x*
касательная
x* - точка касания изокосты с изоквантой, причем задействованы все ресурсы
x1* > 0, x2* > 0
угловая
точка равновесия лежит на одной из осей
одна из координат точки равна 0

Изокоста
- множество планов производства с одинаковыми переменными издержками
Уравнение изокосты
Семейство изокост на плоскости – множество отрезков параллельных прямых с нормалью
Угол наклона изокосты к оси Оx1 определяется отношением цен на ресурсы: tgϕ = – w1/ w2.

Геометрическое решение задачи поиска точки равновесия
при условии

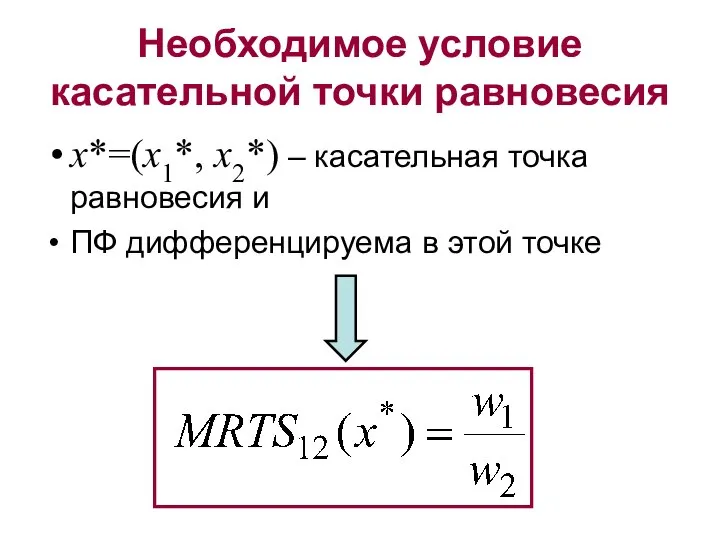
Необходимое условие касательной точки равновесия
x*=(x1*, x2*) – касательная точка равновесия и
ПФ дифференцируема в этой точке

Правило равной производительности ресурсов на единицу затрат
Производитель заменяет один ресурс другим, пока это выгодно.
Отдачи ресурсов в расчете на единицу затрат равны для всех используемых ресурсов.
Рубль затрат в любой ресурс приносит одинаковый эффект.
В рыночной экономике происходит согласование способа производства с соотношением цен на факторы,
производительность факторов (отдача ресурсов) должна соответствовать их стоимости,
в результате ограниченные ресурсы используются самым эффективным способом.

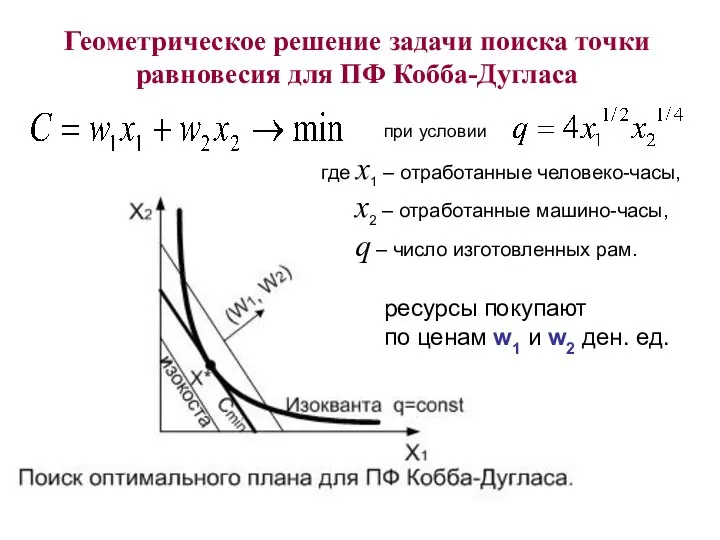
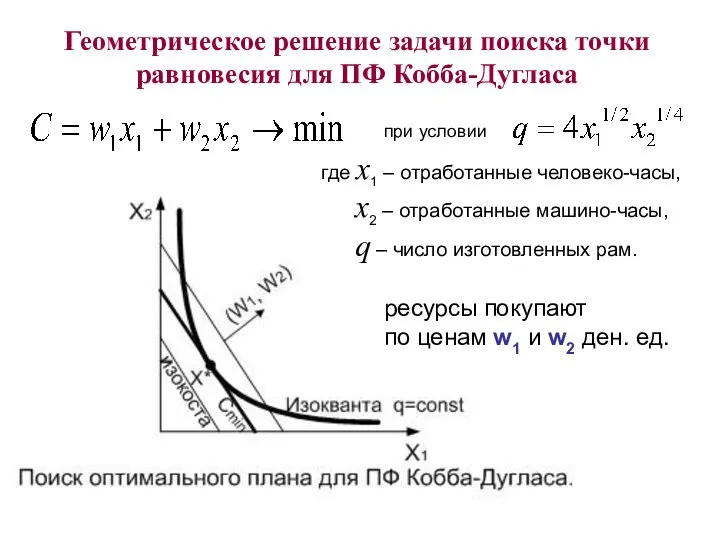
при условии
Геометрическое решение задачи поиска точки равновесия для ПФ Кобба-Дугласа
где x1 – отработанные человеко-часы,
x2 – отработанные машино-часы,
q – число изготовленных рам.
ресурсы покупают
по ценам w1 и w2 ден. ед.

Геометрическое решение задачи поиска точки равновесия
Поиск оптимального плана для линейной ПФ
в одной системе координат построим изокванту и семейство изокост
Для определенности предположим, что
w1/w2 > a1/a2
план х* – самый дешевый, обеспечивающий выпуск q единиц продукции.
Получили угловую точку равновесия argmin G(x) = x* = (0, q/a2).

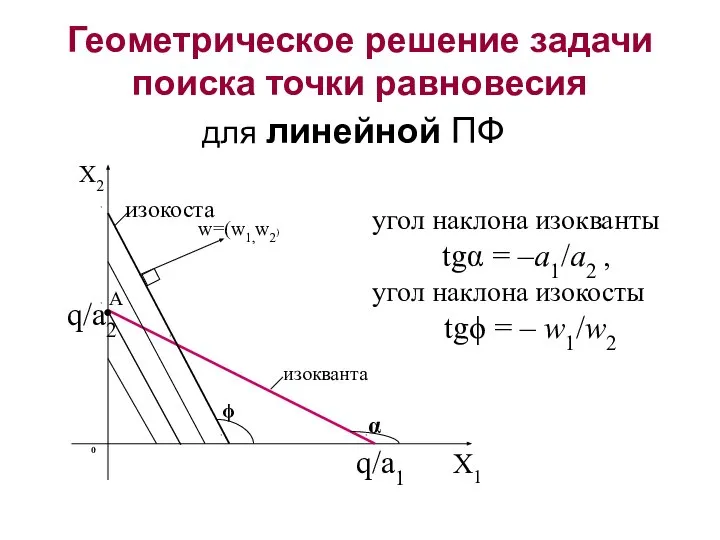
Геометрическое решение задачи поиска точки равновесия
для линейной ПФ
угол наклона изокванты tgα = –a1/a2 ,
угол наклона изокосты
tgϕ = – w1/w2

Если оптимальный план x*=(0, x2*) (невыгодно использовать даже первую единицу первого ресурса), то
Если оптимальный план x*=(x1*, 0), то
Необходимое условие угловой точки равновесия

Функции издержек

Построение функции переменных издержек
Пусть задача минимизации издержек имеет единственное решение:
x*=(x1*, x2*, ..., xn*) - план производства по ресурсам, обеспечивающий выпуск q единиц продукции = оптимальный план по ресурсам = точка равновесия производителя.
функция спроса на ресурсы:
стоимость этих ресурсов денежных единиц.
функция переменных издержек
сопоставляет объему выпуска q и ценам ресурсов w
стоимость плана, обеспечивающего выпуск q единиц продукции с наименьшими переменными издержками,
функция общих издержек

Функция переменных издержек для линейной ПФ
Угловая точка равновесия:
argmin G(x) = x* = (0, q/a2).
Стоимость ресурсов в оптимальном плане Gmin=Сv(q)=w2 q/a2 ден.ед.
В общем случае, для линейной ПФ
функция переменных издержек Сv(q)=min{w1/a1, w2/a2}q.
w1/w2 > a1/a2

при условии
Геометрическое решение задачи поиска точки равновесия для ПФ Кобба-Дугласа
где x1 – отработанные человеко-часы,
x2 – отработанные машино-часы,
q – число изготовленных рам.
ресурсы покупают
по ценам w1 и w2 ден. ед.

Однородные функции
Функция нескольких переменных называется однородной порядка m, если для всех х из некоторой области Х
Если ПФ является однородной порядка m, то
при m=1 ПФ обладает постоянным;
при m>1 ПФ обладает возрастающим
при m<1 ПФ обладает убывающим
эффектом
масштаба

Функция издержек
однородной ПФ
Теорема. Если ПФ является однородной порядка (степени) m, то
функция спроса на ресурсы
где – план по ресурсам, обеспечивающий выпуск единицы продукции с наименьшими переменными издержками
(стоимость плана x1 есть Cv(1)=С1),
функция переменных издержек

Следствие. Если ПФ характеризуется постоянным эффектом масштаба (является однородной степени 1), то она порождает линейную функцию издержек

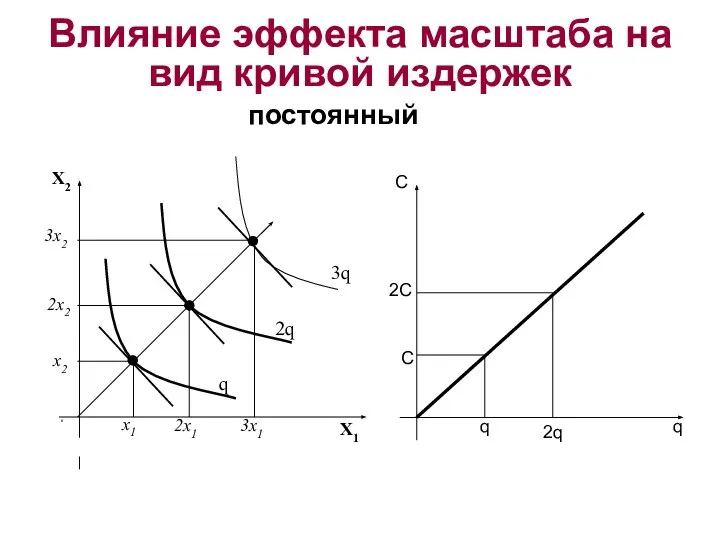
Влияние эффекта масштаба на вид кривой издержек
постоянный

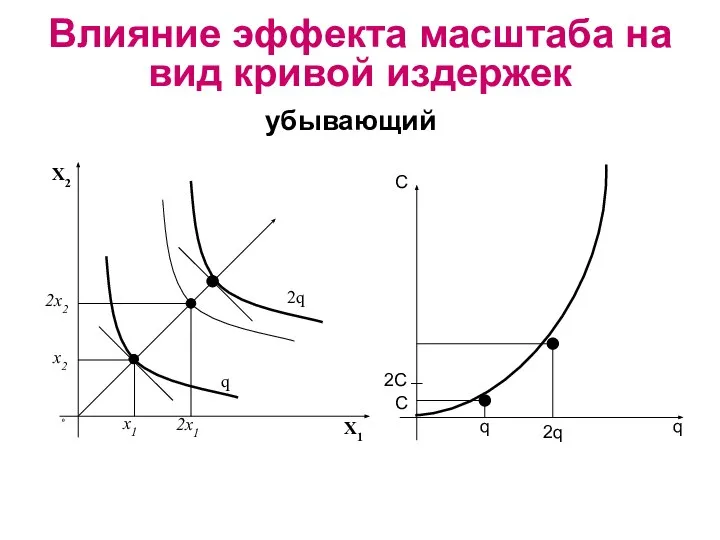
убывающий
Влияние эффекта масштаба на вид кривой издержек

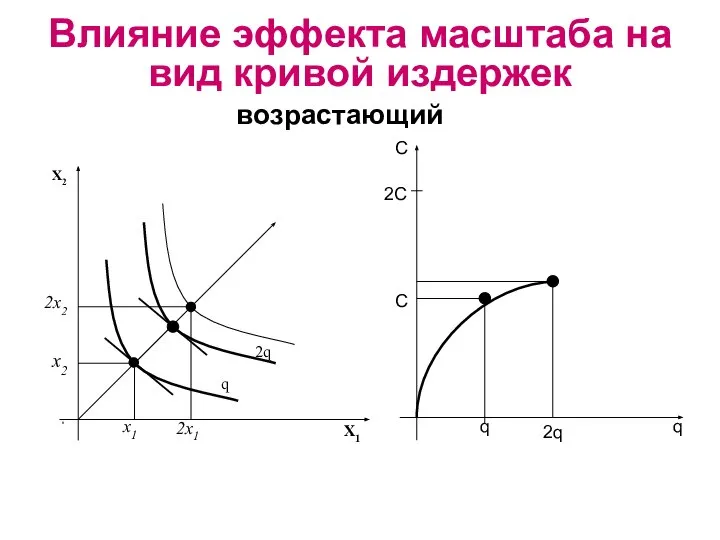
возрастающий
Влияние эффекта масштаба на вид кривой издержек

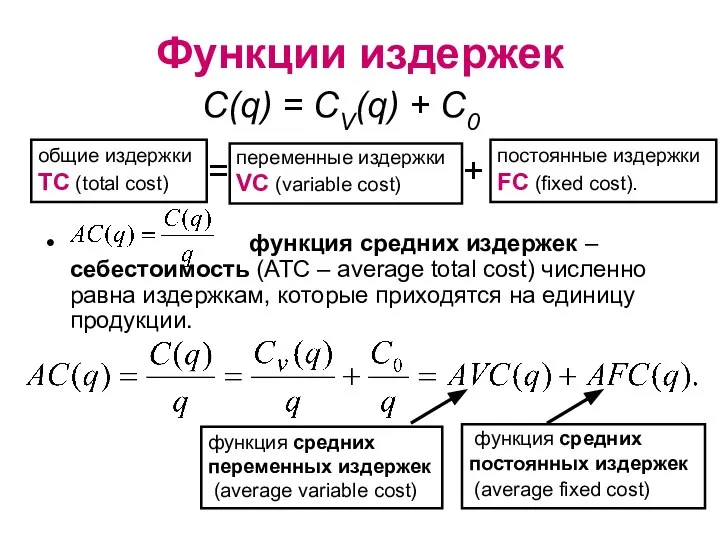
Функции издержек
функция средних издержек – себестоимость (ATC – average total cost) численно равна издержкам, которые приходятся на единицу продукции.
функция средних
переменных издержек
(average variable cost)
функция средних
постоянных издержек
(average fixed cost)
общие издержки
TC (total cost)
постоянные издержки
FC (fixed cost).
переменные издержки
VC (variable cost)
С(q) = CV(q) + С0
=
+

Предельные издержки
- функция предельных издержек.
= MC(q) (marginal cost).
Экономическая интерпретация предельных издержек: величина предельных издержек при данном объеме выпуска показывает, на сколько денежных единиц приблизительно возрастут издержки, если увеличить объем выпуска на единицу

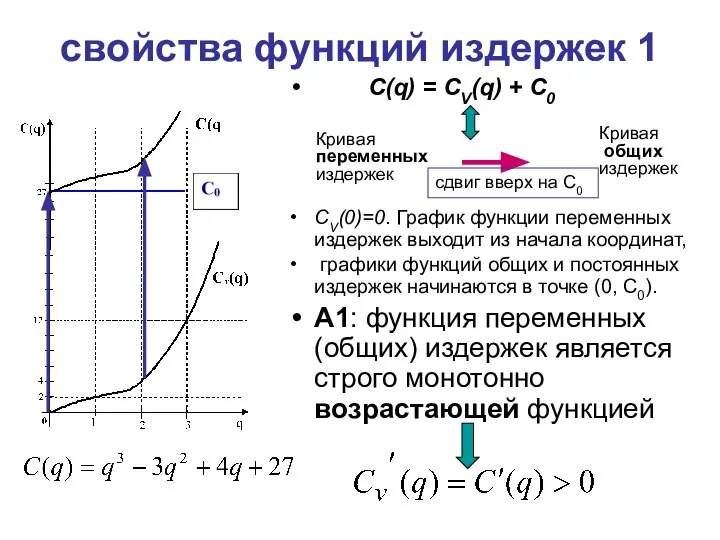
свойства функций издержек 1
С(q) = CV(q) + С0
CV(0)=0. График функции переменных издержек выходит из начала координат,
графики функций общих и постоянных издержек начинаются в точке (0, С0).
A1: функция переменных (общих) издержек является строго монотонно возрастающей функцией
сдвиг вверх на С0
Кривая
переменных
издержек
Кривая
общих
издержек

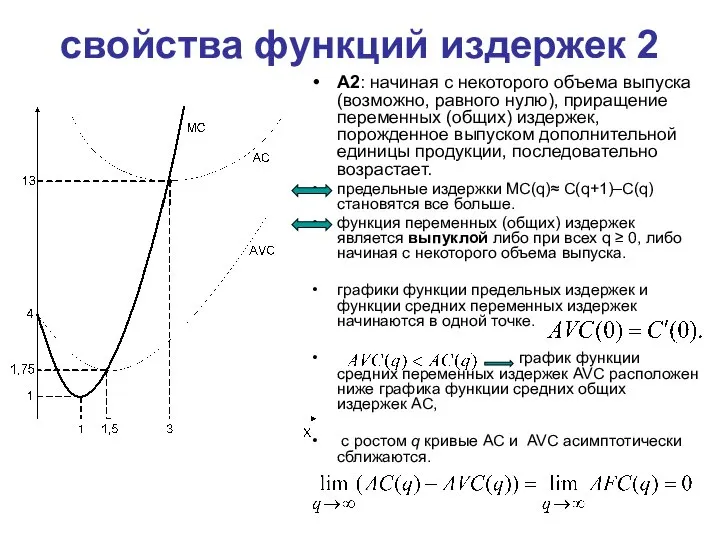
свойства функций издержек 2
A2: начиная с некоторого объема выпуска (возможно, равного нулю), приращение переменных (общих) издержек, порожденное выпуском дополнительной единицы продукции, последовательно возрастает.
предельные издержки MC(q)≈ C(q+1)–C(q) становятся все больше.
функция переменных (общих) издержек является выпуклой либо при всех q ≥ 0, либо начиная с некоторого объема выпуска.
графики функции предельных издержек и функции средних переменных издержек начинаются в одной точке.
график функции средних переменных издержек AVC расположен ниже графика функции средних общих издержек AC,
с ростом q кривые AC и AVC асимптотически сближаются.

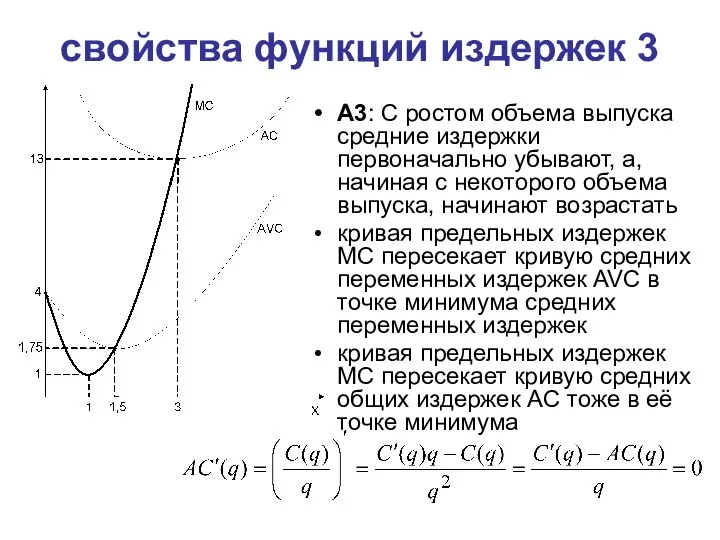
свойства функций издержек 3
A3: C ростом объема выпуска средние издержки первоначально убывают, а, начиная с некоторого объема выпуска, начинают возрастать
кривая предельных издержек MC пересекает кривую средних переменных издержек AVC в точке минимума средних переменных издержек
кривая предельных издержек MC пересекает кривую средних общих издержек AC тоже в её точке минимума

На кривой общих затрат ТС
предельные затраты МС определяются тангенсом угла наклона касательной
средние затраты АС определяются тангенсом угла наклона луча, проведенного из начала координат к кривой
Средние затраты достигают минимума при таком объёме выпуска, когда они равны предельным затратам