Гемодинамика

Лекция 4
Ростов-на-Дону
2012
Гемодинамика

Содержание лекции №4
Вязкость. Ньютоновские неньютоновские жидкости
Ламинарное и турбулентное течение. Число Рейнольдса
Формула Пуазейля
Гемодинамика
Механические свойства биологических тканей

Вязкость . Формула Ньютона
Вязкость (внутреннее трение) – это свойство текучих тел
(жидкостей и газов)
оказывать сопротивление перемещению слоев. Вязкость возникает из-за внутреннего трения между молекулами жидкости.
Река
v+dv
v
dx
Между слоями существует градиент скорости скорость сдвига
=
Течение жидкости по трубе
=

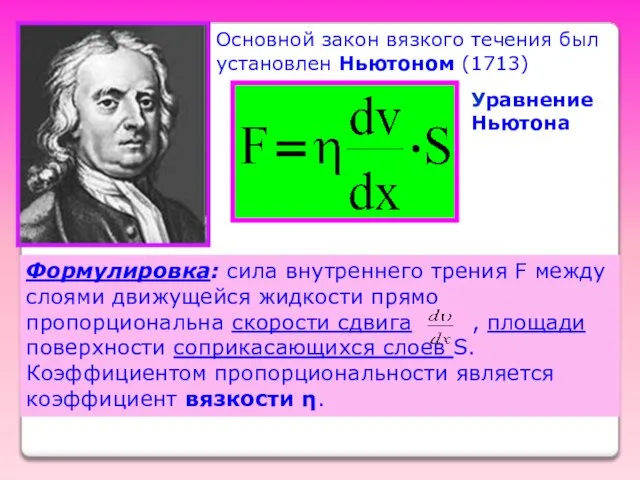
Основной закон вязкого течения был установлен Ньютоном (1713)
Уравнение Ньютона
Формулировка: сила внутреннего трения F между слоями движущейся жидкости прямо пропорциональна скорости сдвига , площади поверхности соприкасающихся слоев S. Коэффициентом пропорциональности является коэффициент вязкости η.

-напряжение сдвига
В реологических характеристиках
уравнение Ньютона имеет вид:
Напряжение сдвига прямо пропорционально скорости сдвига.
η – коэффициент динамической вязкости
[Па]
СИ: [Па•с] = паскаль•секунда
СГС: [П] = пуаз 1 Па•с = 10 П 1мПа•с = 1сП
Реология
-(rheos – течение, поток)
учение о деформации и текучести вещества.

Вязкость зависит от
температуры
Природы жидкости
Формы молекул
Кинематическая вязкость
[Ст] = стокс
Текучесть -
величина,обратная вязкости
t
η
Для жидкостей

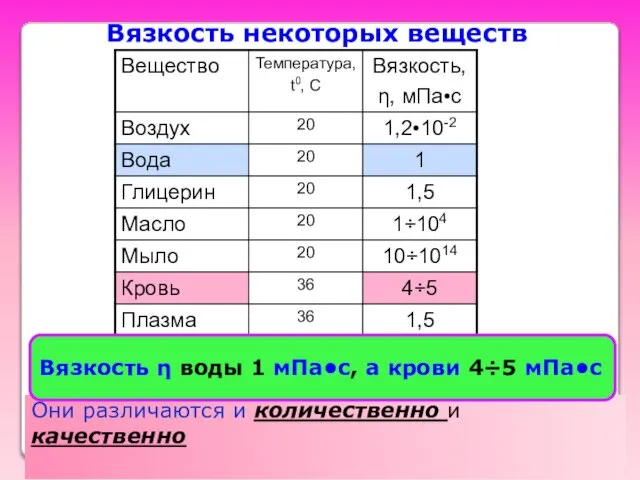
Вязкость некоторых веществ
Они различаются и количественно и качественно
Вязкость η воды 1 мПа•с, а крови 4÷5 мПа•с

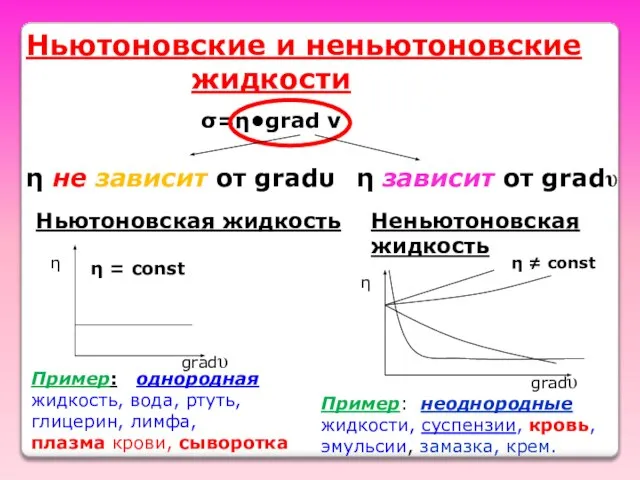
Ньютоновские и неньютоновские
жидкости
Ньютоновская жидкость
σ=η•grad ν
Неньютоновская жидкость
η = const
gradυ
η не зависит от gradυ
η
η зависит от gradυ
Пример: однородная жидкость, вода, ртуть, глицерин, лимфа,
плазма крови, сыворотка
η ≠ const
gradυ
η
Пример: неоднородные жидкости, суспензии, кровь, эмульсии, замазка, крем.

Кровь как неньютоновская
жидкость
Кровь = плазма + форменные элементы
Кровь является неньютоновской жидкостью, так как это суспензия форменных элементов в белковом растворе. Вязкость η крови 4÷5 мПа•с
ВОПРОС:
Каких форменных элементов?
Эритроцитов.
ПОЧЕМУ эритроцитов?
Эритроциты составляют 93%

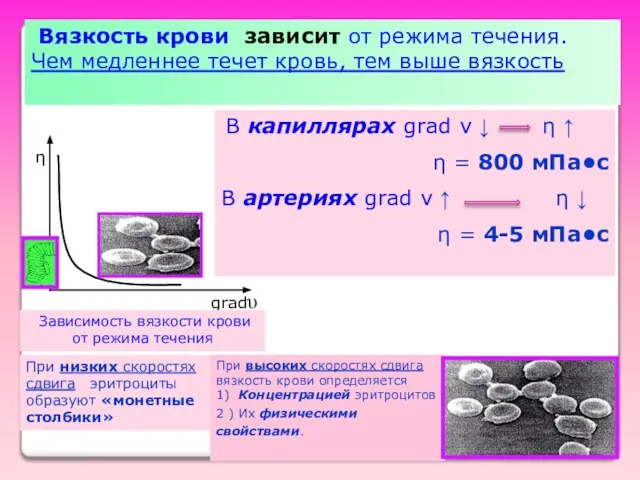
Вязкость крови зависит от режима течения. Чем медленнее течет кровь, тем выше вязкость
η
gradυ
Зависимость вязкости крови от режима течения
В капиллярах grad v ↓ η ↑
η = 800 мПа•с
В артериях grad v ↑ η ↓
η = 4-5 мПа•с
При низких скоростях сдвига эритроциты образуют «монетные столбики»
При высоких скоростях сдвига вязкость крови определяется
1) Концентрацией эритроцитов
2 ) Их физическими свойствами.

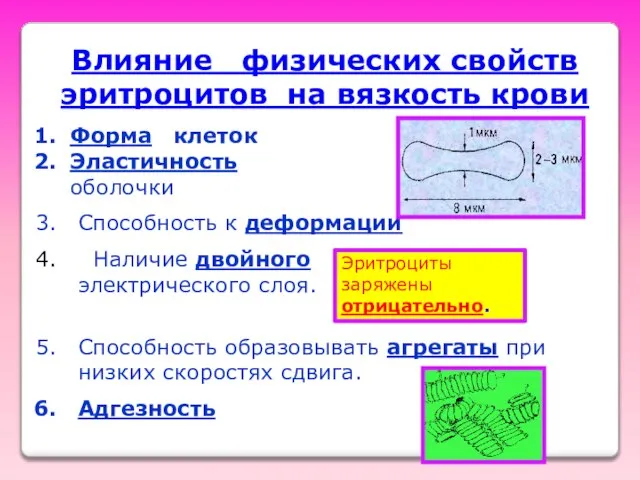
Влияние физических свойств эритроцитов на вязкость крови
Форма клеток
Эластичность
оболочки
Способность к деформации
Наличие двойного
электрического слоя.
Способность образовывать агрегаты при
низких скоростях сдвига.
Адгезность
Эритроциты заряжены отрицательно.

Сыворотка – это
плазма без фибриногена η=1,1мПа•с
Плазма крови – водно-солевой белковый раствор.
Плазма – ньютоновская жидкость. η=1,2мПа•с
Эта цифра вязкости при 370С. Что с ней произойдет при повышении температуры до 410С ?
Вопрос:
Понизится на 10%

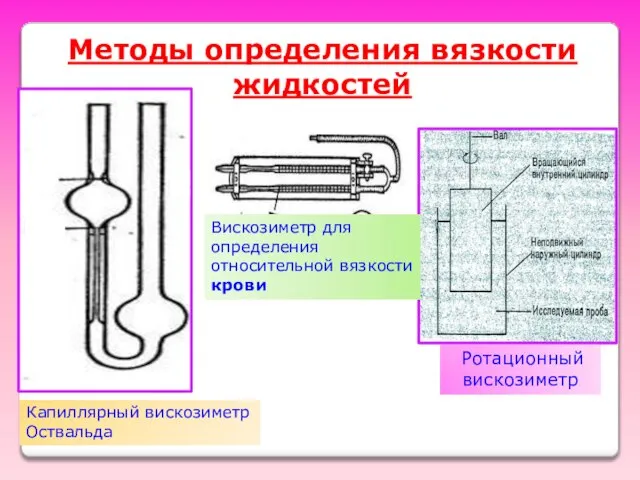
Методы определения вязкости жидкостей
Капиллярный вискозиметр Оствальда
Ротационный вискозиметр
Вискозиметр для определения относительной вязкости крови

Вискозиметр VT550 - высокоточная модель с широким диапазоном измерения, ручной или автоматический режим
под управлением компьютера.
Ротационный вискозиметр Rheotest RV2.1
Наиболее простая модель ротационного вискозиметра,
Устройство работает без применения персонального компьютера, имеет аналоговый дисплей и выход на самописец.
Экспресс-анализатор-вискозиметр ротационный

Стационарный поток
Стационарный поток это такой поток, когда
через каждый уровень поперечного сечения, протекает одинаковый объем жидкости
Условие стационарности
потока Q=const
Q- объемная скорость – это объем жидкости, протекающий через поперечное сечение за единицу времени.

Ламинарное и турбулентное течения
Ламинарное течение- это слоистое течение. Слои жидкости движутся параллельно, не смешиваясь между собой
Турбулентное течение – это вихревое течение- жидкости сопровождающееся перемешиванием слоев, обусловленным образованием вихрей. Скорость частиц непрерывно меняется.

Характер течения жидкости определяется числом Рейнольдса
РЕЙНОЛЬДС, ОСБОРН
(1842–1912),
Ламинарное течение переходит в турбулентное, когда введенное им число Рейнольдса превышает критическое значение.
Величина безразмерная
Если Re < Reкр => Ламинарное течение
Если Re > Reкр =˃ Турбулентное течение
Reкрит. (H2O)=2300 Reкрит.(кровь) = 970 ± 80.
ρ- плотность;
v – скорость;
d- диаметр сосуда:
η - вязкость

Re – критерий подобия двух потоков:
Два потока считаются тождественными, если равны числа Рейнольдса.
Физический смысл числа Рейнольдса:
Re (капилляры)<<1 Re =10-3 - мало (вязкость ↑)
Re (артерии)>>1 Вязкость инерция ↑
ν
V

Формула Пуазейля
Пуазейль Жан Мари французский
врач + физик+ физиолог
Преподавал медицинскую физику
Пуазейль
1799-1869

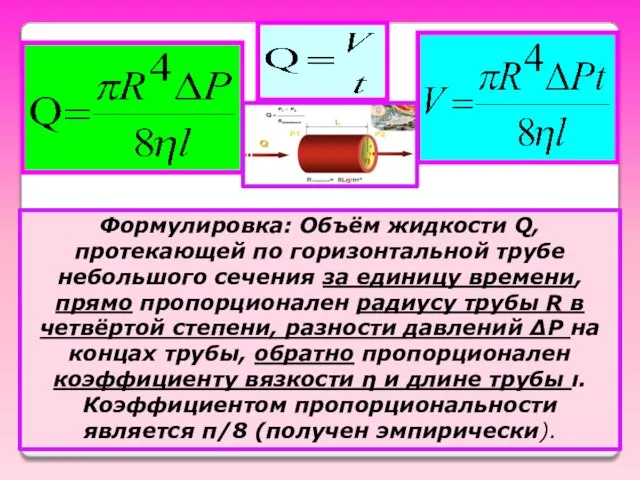
Формулировка: Объём жидкости Q, протекающей по горизонтальной трубе небольшого сечения за единицу времени, прямо пропорционален радиусу трубы R в четвёртой степени, разности давлений ∆P на концах трубы, обратно пропорционален коэффициенту вязкости η и длине трубы ι. Коэффициентом пропорциональности является π/8 (получен эмпирически).

Гидравлическое сопротивление
=>
Основное уравнение
гемодинамики
Перепад давлений прямо пропорционален гидравлическому сопротивлению

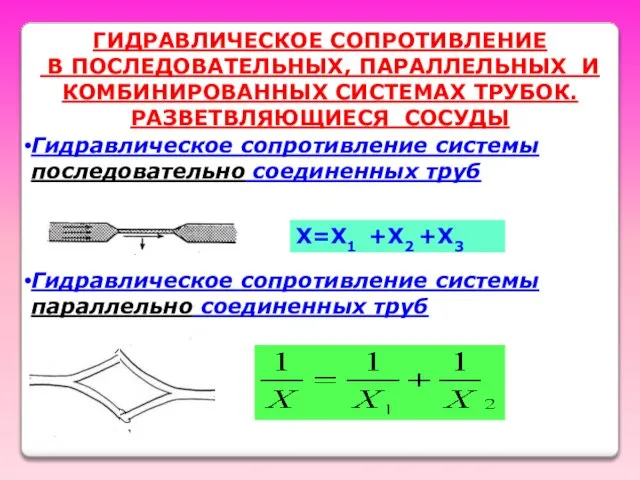
ГИДРАВЛИЧЕСКОЕ СОПРОТИВЛЕНИЕ
В ПОСЛЕДОВАТЕЛЬНЫХ, ПАРАЛЛЕЛЬНЫХ И КОМБИНИРОВАННЫХ СИСТЕМАХ ТРУБОК. РАЗВЕТВЛЯЮЩИЕСЯ СОСУДЫ
Гидравлическое сопротивление системы последовательно соединенных труб
Х=Х1 +Х2 +Х3
Гидравлическое сопротивление системы параллельно соединенных труб

Сужение сосуда
Скорость потока
возрастает
Сопротивление
увеличивается
S٠υ =const
↑∆P=Q٠x↑
Перепад давлений увеличивается

Расширение сосуда
Скорость потока
уменьшается
Сопротивление падает
Перепад давлений уменьшается
S٠υ =const
∆P=Q٠x

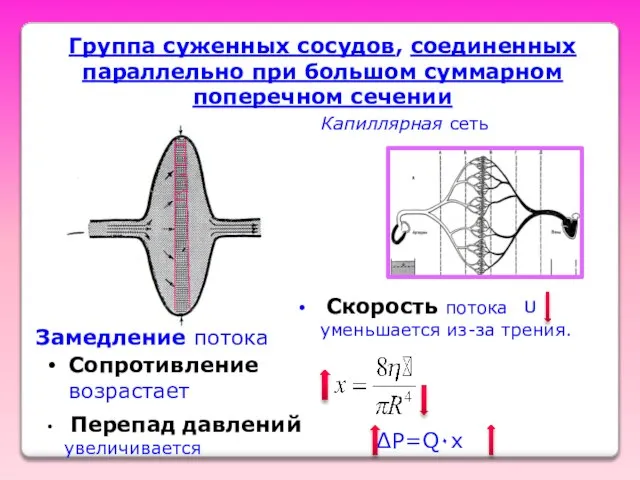
Группа суженных сосудов, соединенных параллельно при большом суммарном поперечном сечении
Замедление потока
Скорость потока уменьшается из-за трения.
Сопротивление
возрастает
υ
Перепад давлений увеличивается
∆P=Q٠x
Капиллярная сеть

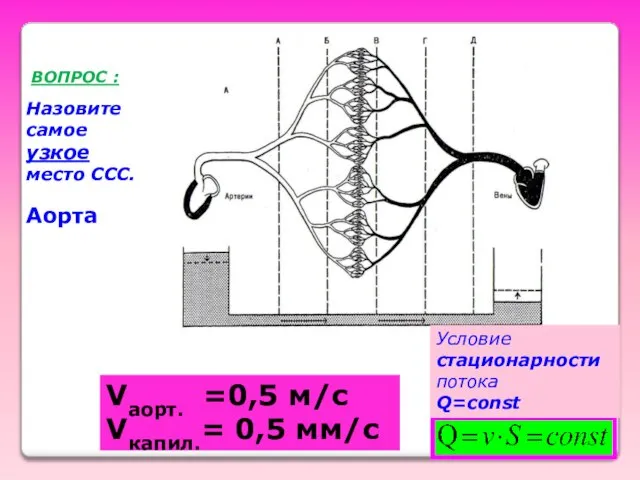
Vаорт. =0,5 м/с
Vкапил.= 0,5 мм/с
ВОПРОС :
Аорта
Назовите самое узкое место ССС.
Условие стационарности
потока Q=const

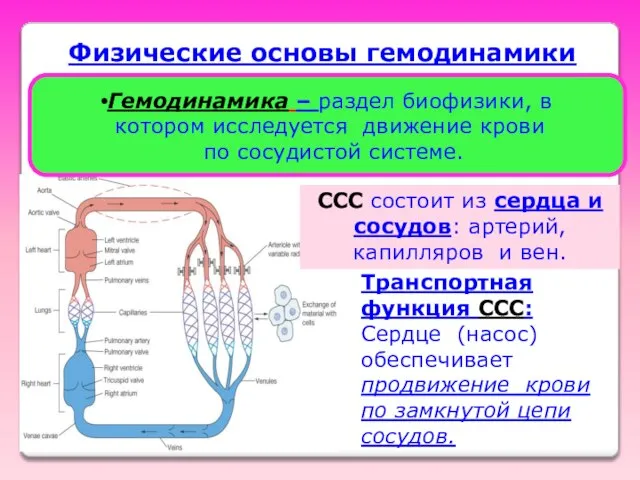
Транспортная функция ССС:
Сердце (насос) обеспечивает продвижение крови по замкнутой цепи сосудов.
Физические основы гемодинамики
Гемодинамика – раздел биофизики, в
котором исследуется движение крови
по сосудистой системе.
ССС состоит из сердца и сосудов: артерий, капилляров и вен.

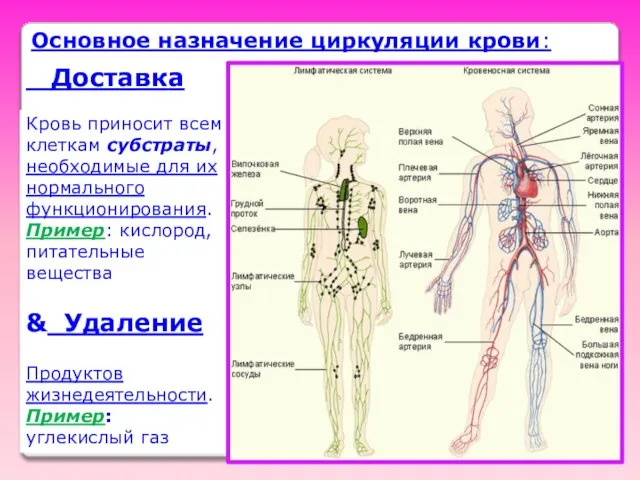
Основное назначение циркуляции крови:
Доставка
Кровь приносит всем клеткам субстраты, необходимые для их нормального функционирования.
Пример: кислород, питательные вещества
& Удаление
Продуктов жизнедеятельности.
Пример:
углекислый газ

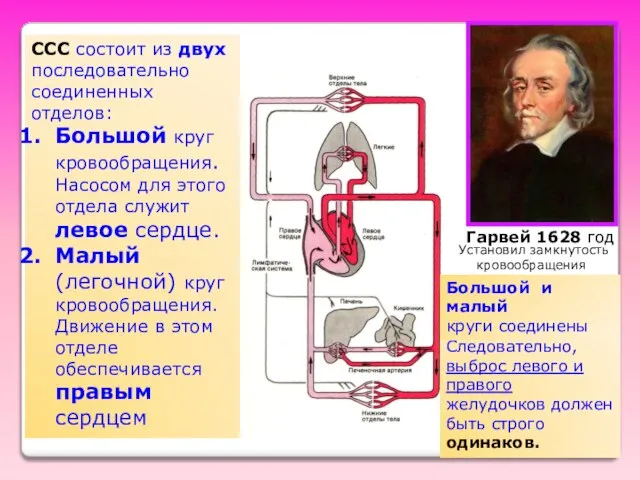
ССС состоит из двух последовательно соединенных отделов:
Большой круг кровообращения. Насосом для этого отдела служит левое сердце.
Малый(легочной) круг кровообращения. Движение в этом отделе обеспечивается правым сердцем
последовательно Следовательно, выброс левого и правого желудочков должен быть строго одинаков.
Гарвей
1628 год
Большой и малый
круги соединены
Установил замкнутость
кровообращения

Ударный объем крови
Это объем крови, который выталкивается из сердца за одно сокращение Vуд равен
600 мл
6 л
Столовая ложка 15 г
6 мл
60 мл
Ответ:
60 мл
ВОПРОС:

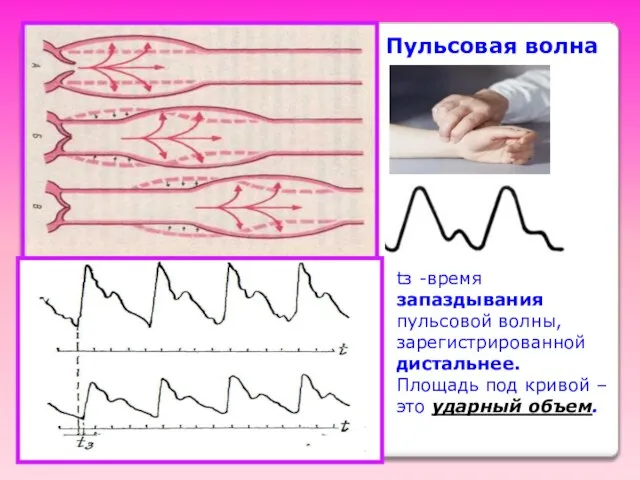
Пульсовая волна, скорость ее распространения
Пульсовая волна - это волна деформации стенок артерии.
Пульсовая волна – это распространяющаяся по аорте и артериям волна повышенного давления, вызванная выбросом крови из левого желудочка в аорту в период систолы.
Причина: упругость аортальной стенки
В китайской литературе пульс сравнивают с плавающей по воде шелковой тканью.

tз -время запаздывания пульсовой волны, зарегистрированной дистальнее.
Площадь под кривой – это ударный объем.
Пульсовая волна

СРПВ –количественный показатель упругих свойств артерии.
Формула Моенса- Кортевега
Скорость распространения пульсовой волны v
Е –модуль Юнга
h- толщина стенки
d –диаметр сосуда
ρ – плотность крови
В норме 5-10 м/с.
Что происходит с СРПВ с возрастом?
Она увеличивается

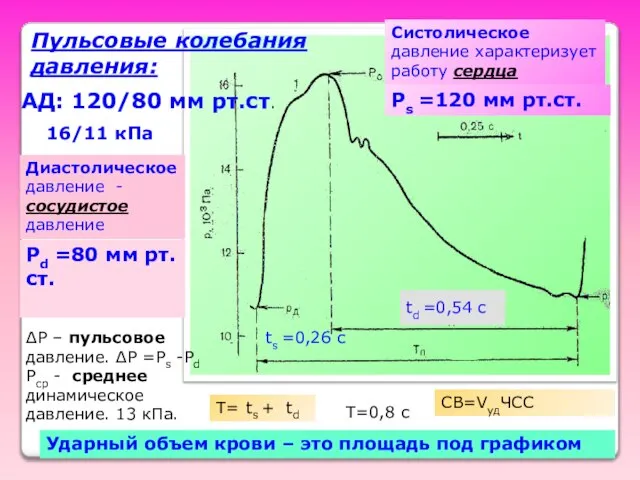
Давление крови в артериях колеблется от максимального во время сокращения сердца (систолы) до минимального во время расслабления (диастолы).
При каждом сердцебиении давление крови поднимается до систолического уровня, а между ударами падает до диастолического уровня
Поэтому артериальное давление определяют как максимальное/минимальное значения (систолическое/диастолическое). Обычно его измеряют в миллиметрах ртутного столба.
В норме 120/80 мм рт.ст. для здоровых взрослых людей.
ВОПРОС:
А в комнате 760 мм рт.ст. – в 5 раз больше, и мы живы.
Катакрота
Анакрота

АД: 120/80 мм рт.ст.
16/11 кПа
Систолическое давление характеризует работу сердца
Диастолическое давление -сосудистое давление
Ps =120 мм рт.ст.
Pd =80 мм рт.ст.
ts =0,26 с
td =0,54 с
T=
ts +
td
T=0,8 с
СВ=VудЧСС
Ударный объем крови – это площадь под графиком
ΔР – пульсовое давление. ΔР =Ps -Pd
Рср - среднее динамическое давление. 13 кПа.
Пульсовые колебания давления:

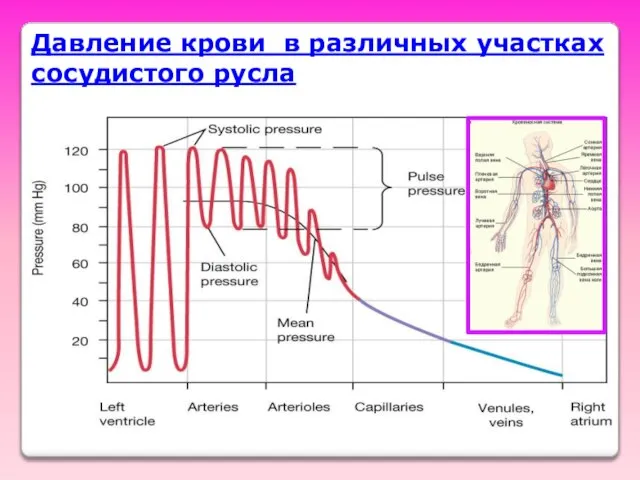
Давление крови в различных участках сосудистого русла

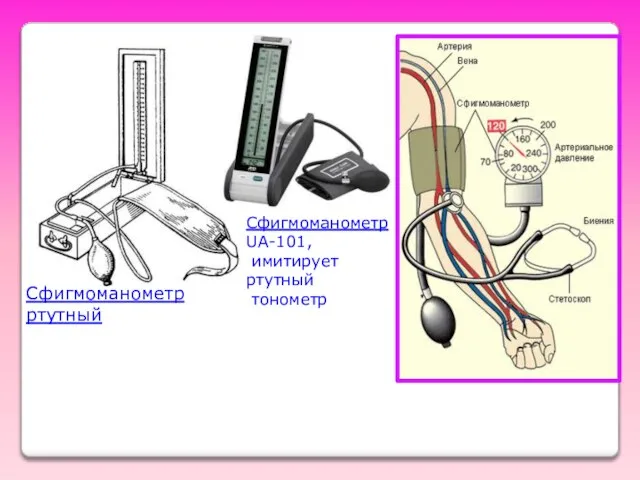
СФИГМОМАНОМЕТР=
= Манжета +груша + манометр
Физические основы клинического метода измерения давления крови.
Основан на измерении внешнего давления, необходимого, чтобы пережать артерию.

Сфигмоманометр
ртутный
Сфигмоманометр
UA-101,
имитирует ртутный
тонометр

Метод Короткова
по измерению АД
105-ЛЕТИЕ НАУЧНОГО ОТКРЫТИЯ ХИРУРГА ВОЕННО-МЕДИЦИНСКОЙ АКАДЕМИИ Н.С.КОРОТКОВА, СДЕЛАВШЕГО ЭПОХУ В РАЗВИТИИ МИРОВОЙ МЕДИЦИНЫ
В созвездии имен великих медиков, заслуживших благодарность всего человечества за свои открытия в медицине, нашло свое место имя русского врача Н. С. Короткова.
8 ноября 1905 года Коротков (ему был 31 год) в своем докладе на «Научном Совещании Клинического военного госпиталя Военно-медицинской академии» сообщил об открытом им звуковом методе бескровного определения максимального и минимального артериального давления (АД) у
человека.
Korotkoff’s method.

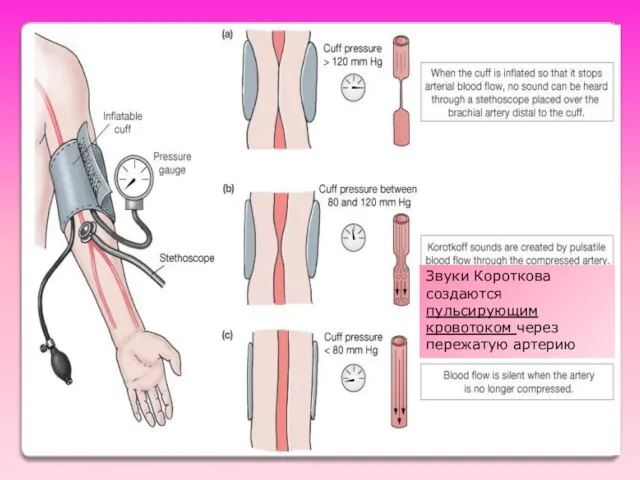
Измерение артериального давления методом Короткова (аускультативный метод)
Основан на возникновении турбулентного течения, когда давление в манжете станет равным систолическому давлению.

Звуки Короткова создаются пульсирующим кровотоком через пережатую артерию

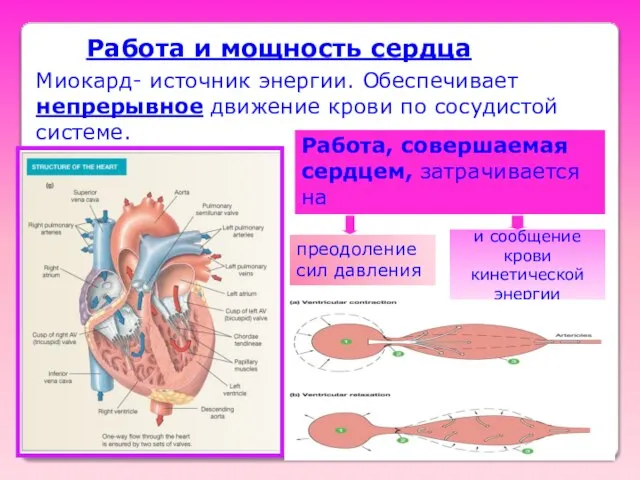
Работа и мощность сердца
Миокард- источник энергии. Обеспечивает непрерывное движение крови по сосудистой системе.
Работа, совершаемая сердцем, затрачивается на
преодоление сил давления
и сообщение крови кинетической энергии

Работа левого желудочка
Работа правого желудочка
Апр = 0,2 А лев.
Всего: Работа сердца равна
Р – среднее динамическое давление. 13 кПа
V – ударный объем крови. 70 мл
Плотность крови 1050 кг/м3
-скорость кровотока 0,5 м/с

Мощность сердца
Больше или меньше мощность сердца, чем мощность электробритвы?
ОТВЕТ:
12 Вт

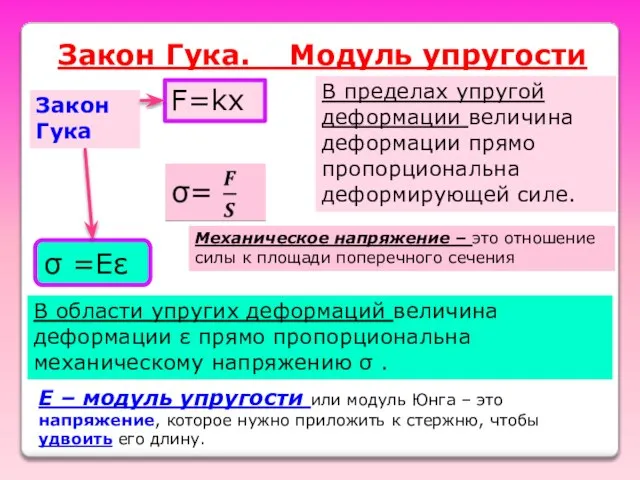
Закон Гука. Модуль упругости
Закон
Гука
σ =Еε
В пределах упругой деформации величина деформации прямо пропорциональна деформирующей силе.
F=kx
Механическое напряжение – это отношение силы к площади поперечного сечения
В области упругих деформаций величина деформации ε прямо пропорциональна механическому напряжению σ .
Е – модуль упругости или модуль Юнга – это напряжение, которое нужно приложить к стержню, чтобы удвоить его длину.

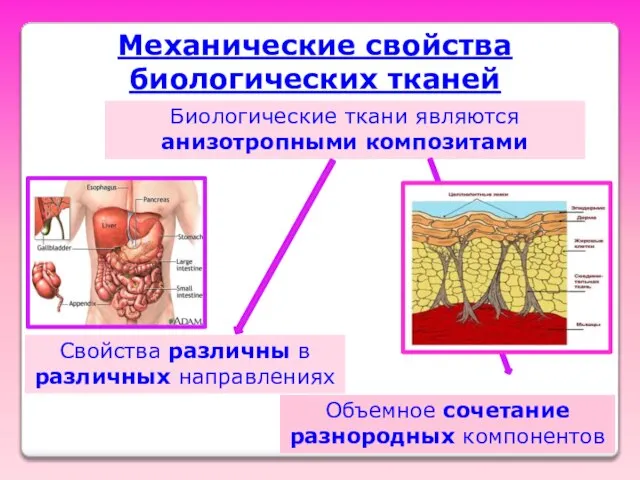
Механические свойства биологических тканей
Биологические ткани являются
анизотропными композитами
Свойства различны в различных направлениях
Объемное сочетание
разнородных компонентов

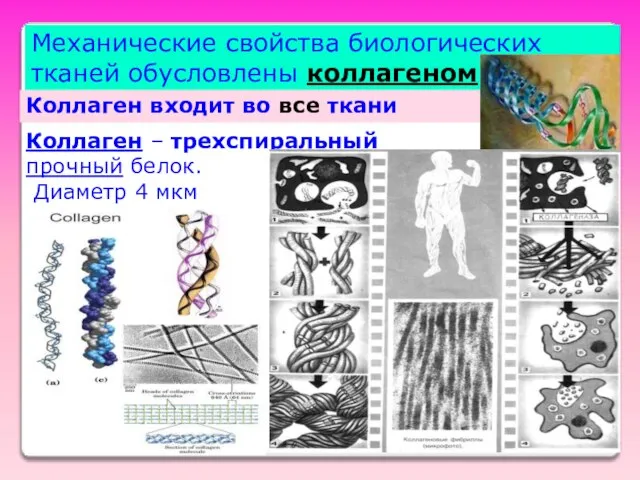
Механические свойства биологических тканей обусловлены коллагеном
Коллаген – трехспиральный
прочный белок.
Диаметр 4 мкм
Коллаген входит во все ткани

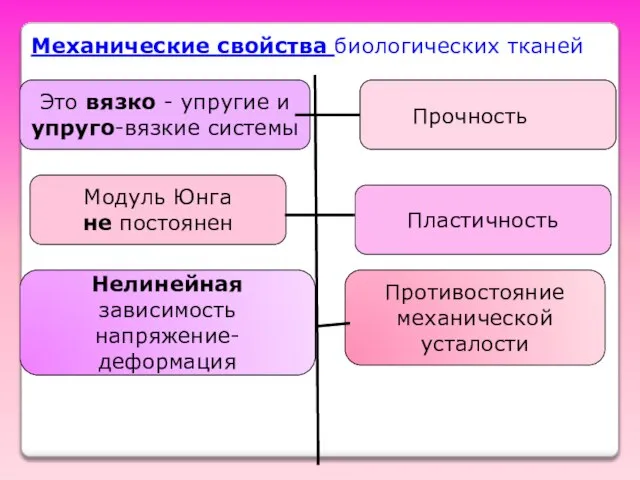
Механические свойства биологических тканей
Это вязко - упругие и
упруго-вязкие системы
Прочность
Модуль Юнга
не постоянен
Пластичность
Противостояние
механической
усталости
Нелинейная зависимость
напряжение-деформация

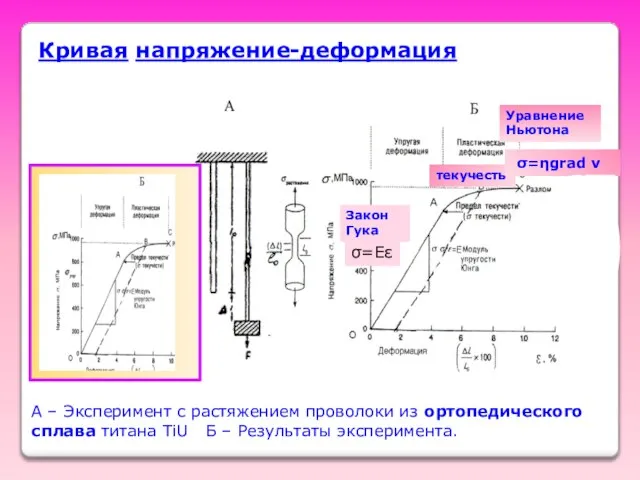
Кривая напряжение-деформация
Кривая напряжение-деформация
A – Эксперимент с растяжением проволоки из ортопедического сплава титана TiU Б – Результаты эксперимента.
Закон
Гука
σ=Еε
текучесть
Уравнение Ньютона
σ=ηgrad v

Механические модели живых тканей

Упругие и прочностные свойства
костной ткани
Это твёрдое упругое тело. ρ=2,4٠103 кг/м3
1/3 коллаген
(орг.)
2/3 гидроксиапатит (неорг.)
Минеральные соли Ca, P
Волокнистая структура коллагеновой матрицы пронизана игольчатыми кристаллами гидроксиапатита. Там кальций. Он держит воду. Кость гидрофильна.
Роль коллагена:
Придает вязкость.

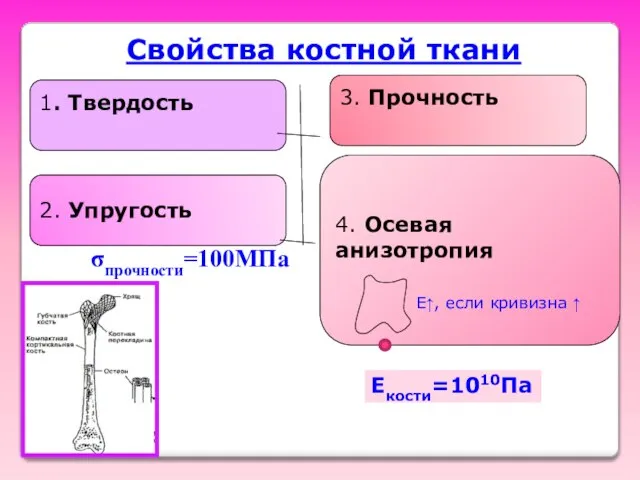
Свойства костной ткани
1. Твердость
2. Упругость
3. Прочность
4. Осевая анизотропия
E↑, если кривизна ↑
σпрочности=100МПа
Eкости=1010Па

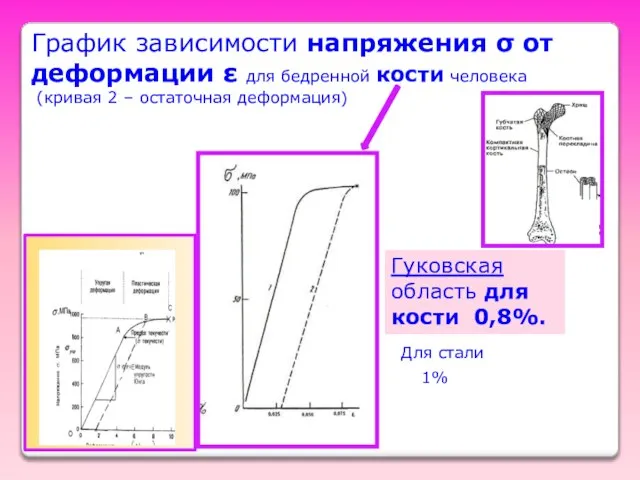
График зависимости напряжения σ от деформации ε для бедренной кости человека
(кривая 2 – остаточная деформация)
Гуковская область для кости 0,8%.
Для стали
1%

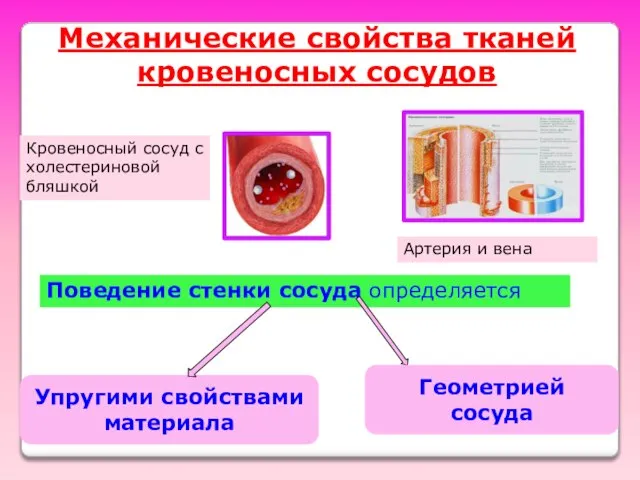
Поведение стенки сосуда определяется
Упругими свойствами
материала
Геометрией сосуда
Механические свойства тканей кровеносных сосудов
Кровеносный сосуд с холестериновой бляшкой
Артерия и вена

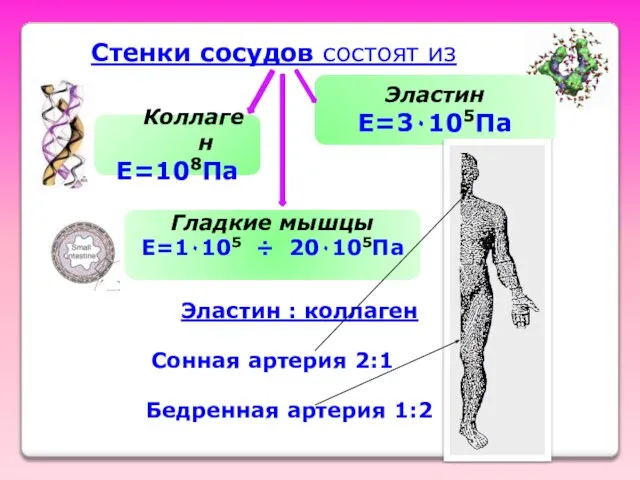
Стенки сосудов состоят из
Коллаген
Е=108Па
Эластин
Е=3٠105Па
Гладкие мышцы
Е=1٠105 ÷ 20٠105Па
Эластин : коллаген
Сонная артерия 2:1
Бедренная артерия 1:2

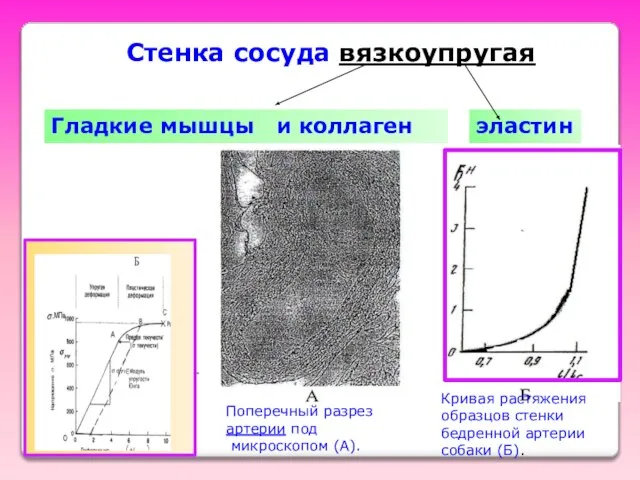
Стенка сосуда вязкоупругая
Гладкие мышцы и коллаген
эластин
Поперечный разрез
артерии под
микроскопом (А).
Кривая растяжения образцов стенки бедренной артерии собаки (Б).

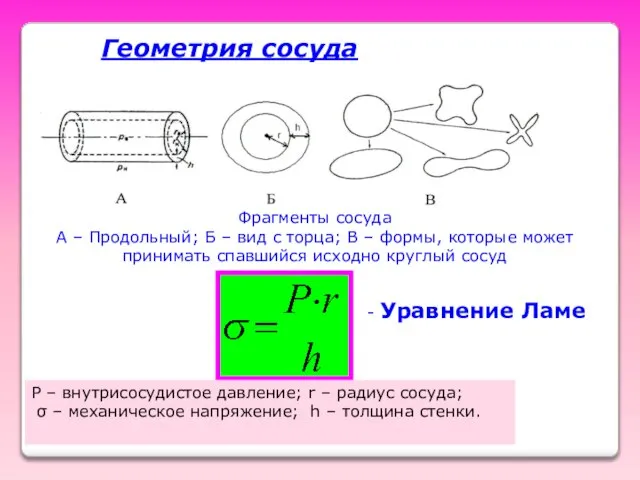
Геометрия сосуда
Фрагменты сосуда
А – Продольный; Б – вид с торца; В – формы, которые может принимать спавшийся исходно круглый сосуд
- Уравнение Ламе
P – внутрисосудистое давление; r – радиус сосуда;
σ – механическое напряжение; h – толщина стенки.